Modelling the Impregnation of a Pressure-Tight Casting

Download PDF

Abstract

Pressure tightness is important for many die-cast aluminium castings, but the interconnected porosity formed in the aluminium alloy high-pressure die castings (HPDC) can form a network connecting several surfaces of the casting, especially as a result of machining after casting. The resulting potential leakage path can be imagined as a series of discontinuities varying in size over wide limits, where voids of different volumes are connected by channels of smaller cross section. Although vacuum impregnation is often used to ensure pressure-tightness is a robust technology, cavity systems through the casting can still cause leakage after impregnation. This study addresses the issues of the impregnation of discontinuities with a complex geometry. The elementary part of a complex cavity geometry consists of a cavity and a capillary channel. We estimated the limited permeability of the capillary section using a mathematical model based on the Hagen–Poiseuille equation. The calculation results prove that the degree of filling of the cavity with a capillary section is basically a function of the geometrical characteristics of the cavity, primarily the radius of the capillary. If the cavity system also contains a section with a diameter of less than 28 μm, impregnation does not necessarily ensure the gas tightness of the casting. Depending on the radius of the capillary, the impregnation of a cavity of a given volume and connected to the surface through a capillary section of a given length can produce three different results. Above a certain capillary radius, filling is complete, below a certain capillary radius only the capillary itself will contain resin, and between the two limit values, the partial impregnation of the cavity is expected but the capillary section is not filled.

Introduction

Characteristics of the Cavity System Causing the Leakage

During the solidification of aluminium castings, the reduction of the specific volume and gas-dissolving capacity of the base metal results in porosity. The porosity of a high-quality casting can be reduced to 0.5–1% and even below that with melt treatment1 and casting techniques.2,3,4,5 These gas inclusions formed during solidification later have an adverse effect on many properties of the finished part.6,7

Porosity can be regarded as a set of spherical voids characteristic of gas inclusions, and cavities of irregular geometry formed as a result of shrinkage. In quality castings, for example pressure-tight castings, the equivalent diameter of the individual cavities is between a few μm and a few tenths of a mm based on micro-computed tomography (micro-CT)8,9,10,11,12 and metallographic13,14,15,16 tests. In a volume of 1 mm3, sometimes up to 50–70 cavities are detected. The size distribution of discontinuities can be described with a lognormal function; the maximum value, i.e. most voids, is in the order of 10 μm.11,12,17 Cavities can be separate, but can also be connected. Detecting the real connected network18 in the cavity system is problematic with both destructive and non-destructive methods, as it is a complex spatial network of capillary-like channels with a small cross section and dimensions below the resolution of CT.11,13,19 This means that the porosity cavity system can be considered a complex network of smaller and larger separated and interconnected discontinuities with a highly variable cross section.

Shrinkage cavities are more likely to occur in sections with larger wall thicknesses, and this is also where the largest cavities are usually found.20,21 Experience shows that in volume parts critical from the point of view of porosity, there can also be voids with a volume of a few tenths of a cm3.22 Due to rapid cooling and the high-temperature gradient, the outer part of the casting, which is close to the surface, usually has a denser structure, and therefore, it is less likely that shrinkage cavities extend to the cast surface. (The phenomenon of leakage through the bifilm oxide film is not investigated in this study.) Branches and extensions of an originally closed shrinkage cavity can reach the vicinity of the casting surface and become an open cavity after the machining of the surface. The inner surfaces of holes and threads produced by machining can intersect porosity cavity systems, and therefore, leakage often takes place through holes drilled into the casting later. The final cavity geometry is also affected by the plastic deformation caused by machining, and as a result, the cross section and characteristic diameter of the channels change. Plastic deformation, especially thread forming, often used in the case of aluminium castings, strongly affects the direction and cross section of the hollow part near the surface or near a hole.

A typical example of this is shown in Fig. 1, in which a gas inclusion cut open by drilling runs onto the threaded profile.

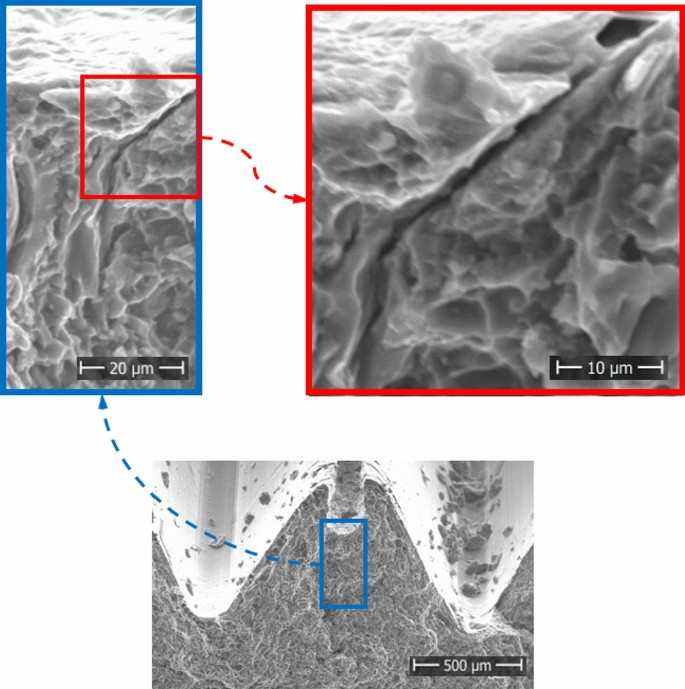
figure 1
Figure 1

The Purpose and Steps of Impregnation

Impregnation is an efficient, robust technology, which can be used to ensure adequate pressure-tightness of castings in the vast majority of cases. Nevertheless, leaks do occur, which is why structures manufactured with gas-tightness requirements (e.g. high-volume die-cast aluminium parts) are usually checked with helium on the assembly line to filter out leaking castings.

The purpose of impregnation is to fill the open cavities in the casting wall with a methacrylate-based impregnation resin, thereby sealing the cavity system in a pressure-tight manner. The castings are impregnated in an autoclave when they are in a completely finished state. The main steps of the process are as follows: (1) vacuuming, (2) immersion in synthetic resin under vacuum, (3) application of atmospheric pressure on the liquid surface of the impregnating resin, (4) lifting the casting out, (5) washing it with cold water, (6) washing it with hot water—during this, the resin hardens around 90–95 °C.

Impregnation begins with vacuuming, the purpose of which is to remove moisture and air in open cavities, and to reduce air pressure in the cavities. Ideally, at the end of vacuuming, the pressure of the gas remaining in the cavity is the same as the pressure of vacuuming. Depending on the geometric characteristics, permeability and volume of the cavity system, the pressures do not necessarily equalize, and pressure higher than ambient pressure may remain in the cavity. The basic condition for the success of step 3, impregnation with the resin, is to achieve the necessary level of vacuum in step 1, since the driving force for filling the cavity with the impregnating agent is, in addition to the capillary effect, the difference between external pressure and the pressure in the cavity. The saturation of the cavity system with resin depends not only on the pressure difference but also on the permeability of the system. The resin flow slows down, i.e. flow resistance increases, mostly because of bottlenecks in the cavity system. Saturation continues until external and internal pressures equalize or the time available in the technology runs out, and the casting is removed from the liquid resin.

There is little reliable literature available on the efficiency of impregnation of cavity systems with complex geometries. According to laboratory impregnation experiments performed on sintered metal alloys with a directed pore structure23, voids below 500 μm are most likely filled with resin and pores below 100 μm are always filled with resin. In practice, leakage can also occur through voids characterized by a diameter of less than 100 μm, which is why it is necessary to use the highly sensitive helium detection method during operational tests.24 We would like to emphasize that the cavity through the casting causing the leakage usually cannot be characterized with a single diameter, as the cross section of the cavity varies greatly along the leakage path.

The result of the impregnation (how saturated the cavities are with resin) is also problematic due to the size and complexity of the cavity system. An example of this is the cavity system in Fig. 2, partially filled with impregnating resin. The cavity on the right side is saturated, and the cavity on the left one is not, presumably due to the small permeability of the capillary indicated by the arrow. Soga et al.22 aimed to detect and examine the impregnation resin filling the cavity system using computed tomography. The procedure is based on the detection of the contrast difference caused by the impregnation resin, the aluminium matrix, and the gases in the cavities. According to the study, in castings with a simple geometry, the filling of the larger cavities of several mm in size can be judged, but the presence of resin in the smaller discontinuities (under 100 μm) cannot be identified—due to the small effective cross section and complicated spatial geometry. Metallographic and scanning electron microscopic examination with UV light can reveal resin-containing and unfilled voids on plane sections of the impregnated casting, but it cannot be clearly decided whether an unfilled void is part of a leakage path or not.25 Of course, the correct selection and using of sealants is also an important criterion.26

figure 2
Figure 2

The present study seeks an answer to how the geometry of a specific open or through cavity system affects the impregnation process. Cavity systems connected to the surface with a channel of small cross section may be critical, since the geometry of the channel system reduces the efficiency of both vacuuming and filling with the impregnating agent. A fundamental question is what geometrical parameters of the cavity system may lead to insufficient impregnation.

Modelling the Impregnation Process

The Geometrical Model

The success and efficiency of impregnation are mostly reduced by the narrow sections in the cavity system. Channels with a uniformly small cross section are filled quickly, but if there is a cavity with a larger volume inside the casting, the material transport required for its impregnation must take place through the narrow sections, which have limited permeability. The time required for vacuuming and filling with liquid resin is greatly influenced by the flow resistance in the small cross-section channel(s).

Based on preliminary calculations, vacuuming and filling a cavity system can be critical if the larger internal cavity created in the casting is connected to the outer surfaces of the casting with a capillary-like channel with a diameter of less than 20–30 μm, or—which is an equivalent situation—to a larger discontinuity connected to the external air. Figure 3a shows a schematic and a geometric model of an internal cavity connected to the machined surfaces by thin channels. For mathematical modelling; that is, for the analysis of the dynamics of vacuuming and filling through the capillaries, it is sufficient to examine the simplified cavity model shown in Fig. 3b. The complex geometry of the cavity system through the casting that develops in reality can be described with several interconnected simplified cavity models. The figure also shows the parameters that determine the impregnation process. These parameters will be interpreted in the next chapter.

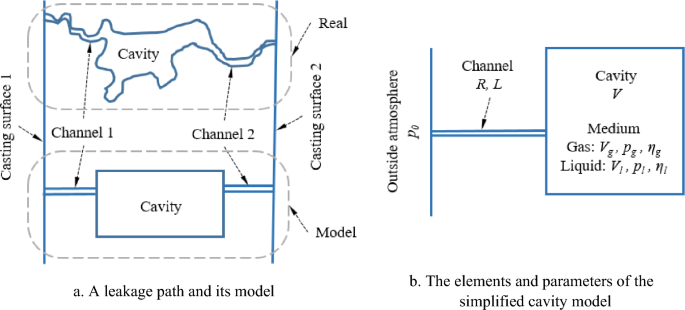
figure 3
Figure 3

Mathematical Model

The relationships described in this chapter can describe the pressure during both the vacuuming and the filling step. The mathematical model describes the change of pressure p in the internal cavity as a function of time when a given external pressure p0 is applied, and the saturation conditions, assuming the simple cavity geometry shown in Fig. 3b. In the vacuuming step, p0 and the volume V contains only gas (air), so the volume Vg of the gas in the cavity is the same as V. In the infiltration operation, p0 and the volume of the cavity (Vg) contains gas and volume Vl contains liquid (resin) and the condition Vg+Vl=V is fulfilled. The results were approximated with a numerical procedure with a finite time step. The time dependence of the pressure values should be determined with a sufficiently small time step Δ� that matches the dynamics of the process.

The assumptions and approximations used in the model are as follows: the volume of the capillary is negligible compared to the volume of the cavity, the capillary is filled in zero time, the flow in the capillary is laminar (Reynolds number—Re < 2300), the impregnating resin behaves as an incompressible liquid, the dynamic viscosity η of the medium (gas, liquid) is independent of the pressure, and the temperature does not change during the process.

The characteristics that are considered constant and the variables interpreted in the time steps are the following:

  • R is the radius of the channel (a uniform cross section is assumed) [m],
  • L is the length of the channel connecting the cavity to the surface [m],
  • V is the volume of the cavity [m3],
  • png��� and ρng��� are the pressure and density of the gas (with the volume Vg) in the cavity in the nth time step [Pa] and [kg/m3],
  • η� is the dynamic viscosity of the medium (gas or liquid) flowing in the capillary [Pa·s],
  • ΔtΔ� time step [s].
  • mg, is the gas mass [kg].

The independent variable is pn0�0�, the external pressure in the nth time step [Pa]. The result of the calculation is pn+1g���+1, the pressure of the gas in the cavity in the (n+1)th ΔtΔ� time step.

As a result of the difference of the external atmospheric pressure pn0�0� and the pressure of the gas in the cavity png���, the I volume flow (gas or liquid) in a capillary of radius R and length L based on the Hagen–Poiseuille formula also takes into account losses:

(1)

I n = π ⋅ ( p 0 n − p g n ) ⋅ R 4 8 ⋅ η ⋅ L [ m 3 / s ]

The mass flow in the capillary (the product of volume flow and density) is:

(2)

M n = I n ⋅ ρ n [ kg / s ]

The mass (gas or liquid)ΔmΔ� travelling through the capillary during time step ΔtΔ� is therefore

(3)

During vacuuming, the change in gas mass according to (3) causes of a pressure drop in the cavity, the volume of which is constant (Vg=V). After the K factor containing constant parameters is introduced, the pressure in the cavity during vacuuming is:

Δ m n = M n ⋅ Δ t = I n ⋅ ρ n ⋅ Δ t [ kg ]

(4)

where

p g n + 1 = p g n + K ⋅ ( p 0 n − p g n ) ⋅ p g n ⋅ Δ t [ Pa ] ,

(5)

During infiltration, the amount (mass) of gas remaining in the cavity after vacuuming does not change. A liquid (resin) flows into the cavity with an intensity corresponding to Eqn. (1). It reduces the volume of the gas, and therefore, the pressure of the gas in the cavity can be calculated with the formula pg·Vg = constant.

If the external atmospheric pressure po is constant vacuuming, the change in the gas pressure in the inner cavity expressed by Eqn. (4) as a function of time can be determined analytically as well (see Appendix).

For time step Δ�, the following inequality is always true:

K = π ⋅ R 4 ⋅ ρ g n 8 ⋅ η g ⋅ L ⋅ m g n = π ⋅ R 4 8 ⋅ η g ⋅ L ⋅ V g

(6)

This means that the volume of the medium leaving or arriving into the cavity within a time step cannot exceed 1% of the volume occupied by the gas. With this condition, the stability of the numerical calculation can be ensured.

The pc capillary pressure resulting from the interaction between the impregnating resin and the capillary can be expressed with the formula

Δ t ≤ 0.01 ⋅ V g I n [ s ]

(7)

where γ is the surface tension of the resin in N/m, and Θ is the wetting angle of the resin on the aluminium casting surface.

Modelling Vacuuming and Filling with Resin

Technological Parameters and Material Properties

In the vacuuming step of the impregnation process, the pressure of the atmosphere surrounding the casting in the autoclave gradually reaches the required vacuum level depending on the performance of the vacuum pumps. In the model calculation, we assume that the reduction of external pressure does not take time. Accordingly, the external vacuum of p0 = 1000 Pa is assumed from the first moment of the process, while the pressure of the gas in the cavity pg corresponds to atmospheric pressure (100 000 Pa). The duration of vacuuming is 10 min, the density of air at atmospheric pressure is ρg = 1.2 kg/m3, and its dynamic viscosity is ηg = 1.8·10-5 Pa s.

After vacuuming, during saturation with resin, the castings are immersed in the impregnating resin in the autoclave, which is also under vacuum, and then, the autoclave is opened, so that there is atmospheric pressure on the surface of the impregnating liquid. The pressure acting on the liquid surface forces the impregnating agent into the vacuumed cavities. The time available for this is usually 6 min. In the calculation, we used the data of Ultraseal Rexeal 100 impregnating resin25: dynamic viscosity is ηl = 0.0045 Pa s, density is ρl = 920 kg/m3, surface tension is γ = 0.031 N/m, and based on our own measurement, the wetting angle of the resin on the cleaned surface of the aluminium casting is Θ = 10°.

At the end of the saturation stage, the castings are removed from the impregnating agent, so atmospheric external pressure continues to act on the system, but the supply of liquid (resin) stops. The last stage of impregnation is washing with cold water and then with hot water. The purpose of the latter is to heat the castings and the impregnating agent to the curing temperature (about 90–95 °C). Both washing operations also serve to remove the impregnating agent from the surfaces of the casting. During intensive washing, the impregnating agent may be washed out of the larger surface cavities before curing. The duration of the washing phase is 4 min.

Calculation Results

We performed the calculation in this chapter with the geometrical data of a cavity system with a realistic size, and the usual technological parameters of vacuum impregnation. Let a cavity with a total volume of 0.1 cm3 (in the critical part of the casting in terms of leakage) be connected to the outer surface with a 0.1 mm long capillary section according to the geometric model of Fig. 1b. Let us examine how the V=100 mm3 cavity is vacuumed and filled with resin through the L=100 μm capillary section depending on capillary radius. Figure 2 shows vacuuming and saturation, as well as the development of pressure and the degree of saturation.

The first 10 min (Fig. 4) is vacuuming, and then, between 10 and 16 min, the casting is filled with the impregnation resin. The blue line indicates the pressure p0 of the external atmosphere, which is 1000 Pa during vacuuming and 100 000 Pa during the saturation stage. The pressure pg of the air in the cavity is shown by the red curve. In the saturation phase (10–16 min), the difference between external pressure p0 and internal pressure pg is indicated separately, marked with a black line. The green line indicates the percentage of the V=100 mm3 cavity filled. Capillary pressure corresponding to the current capillary radius is represented by the black dashed line—it does not change during the process.

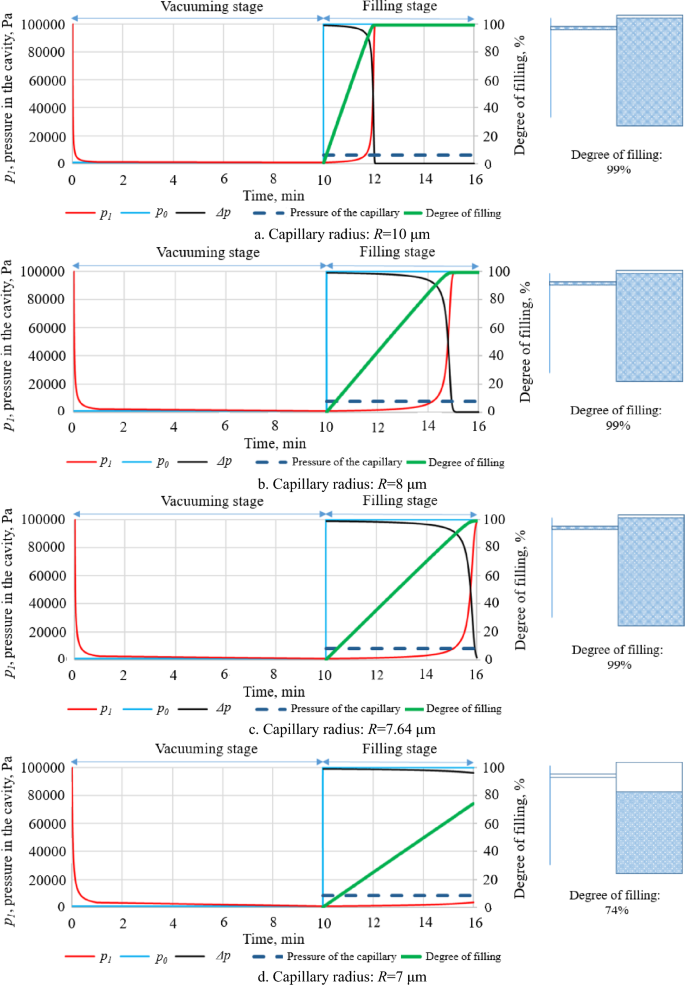
figure 4
Figure 4

Figure 4a shows pressure and degree of filling as a function of time for a capillary radius of R=10 μm. During the vacuuming stage, the pressure in the 100 mm3 cavity approaches the required vacuum level fast, in about half a minute, and saturation with resin also takes place very quickly—it takes about 2 min to reach 99% filling. During saturation, the volume ratio of the resin flowing into the cavity increases (green line), and the pressure of the air remaining in the cavity, with a volume ratio of 1% at the end of the process, reaches external pressure (red line), while the pressure difference decreases to zero (black line). At least 1% of the air remains in the cavity, since the pressure of vacuuming is 1% of atmospheric pressure. The driving force of filling—the difference between external and internal pressure—promotes the flow of resin until the pressure difference equalizes or the time available in the technology expires. In the example of Fig. 4a, both conditions are met. By the end of the impregnation operation, the external and internal pressures are equal, the flow of liquid, and the capillary section is also saturated with resin, as Fig. 4a. shows. Removing the casting from the resin does not cause any change, as both ends of the capillary are at atmospheric pressure. Due to the balance of pressures, it can be assumed that intensive washing does not affect the amount and location of resin in the capillary.

Similar conditions can be expected when the capillary radius is R = 8 μm (Fig. 4b). The vacuum pressure achieved in the cavity approaches the target value (pg = 1005 Pa at the end of the 10th minute) and saturation takes place within the time allowed by the technology, in about 4.8 min. It takes exactly 6 min to fill the cavity in the example shown in Fig. 4c, if the radius of the capillary is R = 7.64 μm. In this case, the pressure difference between the external and inner spaces drops to zero exactly at the end of the saturation stage, while the cavity is almost 99% filled (at the end of the vacuuming stage pg = 1013 Pa). From the above, it follows that if the radius of the capillary section is greater than 7.64 μm, both vacuuming and saturation are completed within the time available in the technology, and the filling of the cavity approaches 99%.

Conditions change considerably if the capillary radius is smaller than 7.64 μm. In the cases shown in Fig. 4d–g, the filling of the cavity decreases drastically with a decrease in capillary radius. The capillary itself does not contain resin after impregnation, as no more resin comes at the end of the 16th min. In this case, the difference between external pressure and the pressure of the cavity exceeds capillary pressure, so after the casting is removed from the resin, external air pressure presses the amount of resin in the capillary into the cavity, and the pressure is equalized through the empty capillary. Gas tightness in these cases cannot be considered adequate, since the cavities are not filled to their full volume with resin and the capillary section is permeable to gases. At the end of impregnation, the water in contact with the casting can also enter the cavity during washing, partly due to the capillary effect and partly due to the difference between external pressure and the pressure in the cavity.

If at the end of the 16th minute, when the casting is removed from the resin, the difference between the external and internal pressure is smaller than the capillary pressure, the resin can remain in the capillary. Figure 4h shows such a case, with the result of the calculation for a capillary radius of R = 1.3 μm. This is because as capillary size decreases, the vacuum achieved in the cavity is worse, while capillary pressure increases. In the present calculation example, the two pressures are the same for a capillary radius of R = 1.51 μm.

Generalization of the Basic Cases of Impregnation

Depending on the radius of the capillary, the impregnation of a cavity connected to the surface through a capillary section can have three different results: above a certain capillary radius, complete filling occurs (A), at a capillary radius below a given limit, only the capillary will contain resin (C), and between the two limits, partial impregnation of the cavity is expected without the capillary part being filled (B). For a more general investigation of the problem, it is advisable to combine the length of the capillary and the volume of the cavity into one parameter, since according to Eqn. (3), they are equivalent in their effect—pressure and degree of filling are the same for the same values of L·V. Figure 3 shows the values of capillary radius separating the three basic cases depending on the combined parameter.

The lines of the diagram divide the plane determined by the product L·V and the capillary radius R into three parts, which represent the above basic cases. The auxiliary lines of the diagram indicate the expected cavity filling for the parameter combinations in range B. If, for example, a cavity with a total volume of 40 mm3 is connected to the surface with a 500 μm long capillary with a radius of 8 μm, the diagram shows at a value of L·V = 20,000 that partial impregnation falling into area B can be expected with 70% filling of the cavity. The same result is obtained if the volume of the cavity is, for example, 56.98 mm3, and the length of the capillary is 351 μm, since the product of the two parameters is also 20,000. In the part above the thick red line, cavity filling is adequate with all parameter combinations (region A), so no leakage is expected.

In the case of parameter combinations below the thick black line, only the capillary is filled, no significant amount of impregnating agent enters the cavity (case C). In the area between the thick red and black lines, partial cavity filling occurs, and therefore, no impregnating resin remains in the capillary (region B) (Fig. 5).

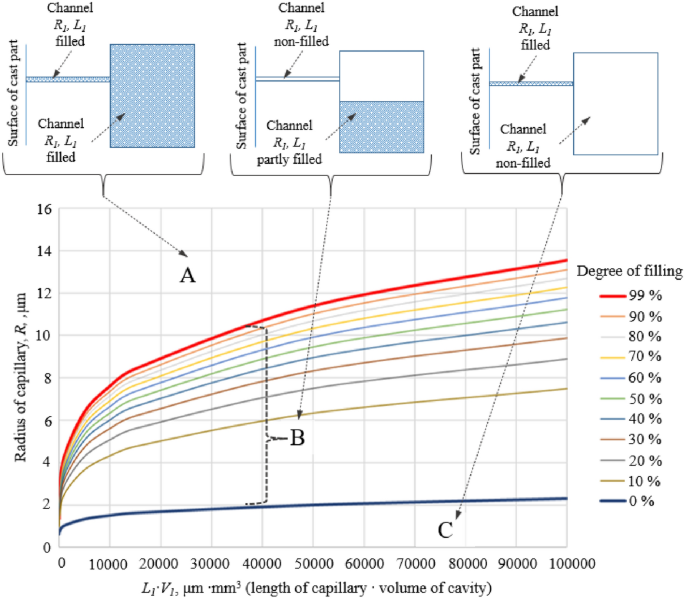
figure 5
Figure 5

In terms of preventing leakage, A is the most favourable, as the filling of 99% of voids and full capillary filling are expected, i.e. impregnation is perfect under the given conditions. Better filling than this can only be achieved by further reducing the vacuum or increasing the external pressure in the filling stage. Cavities characterized by parameter combinations above the red line and containing a capillary section can be sealed leak-free by vacuum impregnation.

The parameter range of area B is quite wide, and depending on the parameter combinations, many different impregnation results are likely. For example, if L·V is 50,000 (a cavity of 50 mm3 and a channel length of 1000 μm) and the capillary has a radius of 11 μm, filling is almost perfect (90%) but if the radius of the capillary is 2.1 μm, impregnation is almost completely ineffective (the capillary does not contain resin in either case). Cavity filling changes drastically in this range, decreasing to 60% at a radius of 10 μm and 10% at a radius of 6 μm. The higher the filling of the cavity, the more likely it is that the cavity system will be pressure-tight, but even 90% filling does not guarantee gas tightness, as the resin can be located in the complex cavity system in such a way that a leakage path remains open. It follows that the result of the impregnation is uncertain in all of the parameter combinations in area B, but the closer we are to the upper border of area B, the more likely gas tightness is.

In region C, the filling of the cavity is essentially zero, but the capillary will be filled with resin. The entire cavity system is in the same condition as before impregnation, only a very short section of the capillary will be sealed. In terms of leakage, the situation is more favourable than in the lower third of area B, since the resin in the capillary at least seals the cavity system. However, if the resin plug in the capillary is later damaged for some reason (e.g. washed out or mixed with water during the washing operation, or its environment is deformed during assembly, e.g. tightening of screws), then the cavity system will most probably leak.

Summary

The study focuses on the impregnation of porosity cavity systems occurring in the inner part of die-cast aluminium alloy castings. Based on measurements,25,27,28 the cavity systems formed by interconnected porosity cavities can be understood as a series of discontinuities of highly varying lengths and cross sections, in which the cavities of different volumes are connected by channels of smaller cross sections. A connected discontinuity inside the casting that does not reach the surface can become an open cavity system, even connecting several casting surfaces, mostly due to machining. Although vacuum impregnation is a very effective technology for ensuring gas tightness, experience shows that through cavity systems can cause leakage even after impregnation. Based on the calculations, the impregnating agent reliably fills cavities if they have a uniform cross section. However, the sealing of leakage paths with variable cross sections, including narrow channels, will not necessarily be successful, since resin has to be transported in sections with a small cross section to fill the entire volume. The elementary part of a cavity system with a complex geometry is the model presented in Fig. 2b. By multiplying this model, the geometry of the cavity system can be modelled in terms of resin flow. The filling of a cavity with a simplified geometry can provide a guideline for the impregnation of real cavity systems.

The following conclusions can be drawn based on the results of model calculations (using vacuum impregnation) with realistically assumed dimensions of the elements of a cavity system:

  • If the leakage path has an almost uniform cross section, problem-free impregnation can be expected regardless of the size and radius of the channel passing through.
  • In the cavity system, larger volume and cross-sectional differences between individual sections make sufficient impregnation less likely.
  • Sections with a smaller cross section in the cavity system also makes insufficient impregnation likely, due to the local limitation of permeability.
  • If the equivalent diameter of the smallest cross section in the cavity system of a complex geometry and variable cross section is over 28 μm (R< 14 μm), the cavities in the casting are 99% filled with resin, i.e. impregnation is perfect (Fig. 5).
  • Full impregnation is expected in the case of cavity geometry parameters in range A in Fig. 5.
  • Partial impregnation with uncertain leakage can be expected in area B indicated in Fig. 5; the degree of filling at a given L·V value depends to a great extent on radius R.
  • In the case of cavity parameters in range C, only the capillary section contains resin. Gas tightness cannot be guaranteed, as possible effects on the capillary section (mixing of the resin with water, mechanical effects) may activate the leakage path.
  • Any effect that makes cross sections with an equivalent radius below 14 μm likely to occur in the cavity system impairs the effectiveness of impregnation. For example, such can be the threading technology used to create the threads in holes in the casting, which can result in local deformation of the leakage paths crossing the hole, thereby reducing the cross section of the hollow part that runs onto the surface.

The developed mathematical model can contribute to the clarification of many technological issues. With it, it can be judged how and to what extent the modification of the parameters of impregnation parameters affects the result of impregnation if there are cavities with capillaries, which make impregnation more difficult. Such impregnation parameters can be the level of vacuum, the pressure applied during saturation above atmospheric pressure, the duration of the technological steps, the viscosity of the resin, etc.

References

  1. L. Pavlak, J.C. Sturm, Reduction of oxide inclusions in aluminum cylinder heads through autonomous designs of experiments. Int. J. Metalcast. 11(2), 174–188 (2017). https://doi.org/10.1007/s40962-016-0096-5Article Google Scholar 
  2. J.P. Weiler, J.T. Wood, R.J. Klassen, E. Maire, R. Berkmortel, G. Wang, Relationship between internal porosity and fracture strength of die-cast magnesium AM60B alloy. Mater. Sci. Eng. A 395(1–2), 315–322 (2005). https://doi.org/10.1016/j.msea.2004.12.042Article CAS Google Scholar 
  3. S.G. Lee, A.M. Gokhale, G.R. Patel, M. Evans, Effect of process parameters on porosity distributions in high-pressure die-cast AM50 Mg-alloy. Mater. Sci. Eng. A 427(2), 99–111 (2006)Article Google Scholar 
  4. M.A. Irfan, D. Schwam, A. Karve, R. Ryder, Porosity reduction and mechanical properties improvement in die cast engine blocks. Mater. Sci. Eng. A 535, 108–114 (2012). https://doi.org/10.1016/j.msea.2011.12.049Article CAS Google Scholar 
  5. F.E. Knight, D.M. Cross, Research into the significance of pressure in the application of impregnation sealant for porous castings in power train components. Die Casting Congress & Exposition. (2015)
  6. Q. Wan, H. Zhao, C. Zou, Effect of micro-porosities on fatigue behavior in aluminum die castings by 3D X-ray tomography inspection. ISIJ Int. 54(3), 511–515 (2014). https://doi.org/10.2355/isijinternational.54.511Article CAS Google Scholar 
  7. A. Nourian-Avval, A. Fatemi, Fatigue life prediction of cast aluminum alloy based on porosity characteristics. Theor. Appl. Fract. Mech. 109, 102774 (2020). https://doi.org/10.1016/j.tafmec.2020.102774Article CAS Google Scholar 
  8. M. Simon, S. Sauerwein, Quality control of light metal castings by 3D computed tomography, in The 15th World Conference on Non-Destructive Testing; Rome, Italy. October 15–21, (2000)
  9. V.A. Jaques, A. Du Plessis, M. Zemek, J. Šalplachta, Z. Stubianová, T. Zikmund, J. Kaiser, Review of porosity uncertainty estimation methods in computed tomography dataset. Meas. Sci. Technol. 32(12), 122001 (2021). https://doi.org/10.1088/1361-6501/ac1b40Article CAS ADS Google Scholar 
  10. S. Carmignato, Computed tomography as a promising solution for industrial quality control and inspection of castings. Metall. Sci. Tecnol. 30(1) (2012).
  11. C. Garb, M. Leitner, M. Tauscher, M. Weidt, R. Brunner, Statistical analysis of micropore size distributions in Al–Si castings evaluated by X-ray computed tomography. Int. J. Mater. Res. 109(10), 889–899 (2018). https://doi.org/10.3139/146.111685Article CAS Google Scholar 
  12. M. Weidt, R.A. Hardin, C. Garb, J. Rosc, R. Brunner, C. Beckermann, Prediction of porosity characteristics of aluminium castings based on X-ray CT measurements. Int. J. Cast Met. Res. 31(5), 289–307 (2018). https://doi.org/10.1080/13640461.2018.1467105Article CAS Google Scholar 
  13. G.R. Nicoletto, Konečná, S. Fintova, Characterization of microshrinkage casting defects of Al–Si alloys by X-ray computed tomography and metallography. Int. J. Fatigue. 41 39–46. (2012). https://doi.org/10.1016/j.ijfatigue.2012.01.006
  14. A. Nourian-Avval, A. Fatemi, Characterization and analysis of porosities in high pressure die cast aluminum by using metallography, x-ray radiography, and micro-computed tomography. Materials 13(14), 3068 (2020). https://doi.org/10.3390/ma13143068Article CAS ADS PubMed PubMed Central Google Scholar 
  15. N. Roy, A. Samuel, F. Samuel, Porosity formation in AI-9 Wt pct Si-3 Wt pct Cu alloy systems: metallographic observations. Metall. Mater. Trans. A 27(2), 415–429 (1996). https://doi.org/10.1007/BF02648419Article Google Scholar 
  16. G. Ran, J.E. Zhou, Metallographic characterization of porosity in a cast aluminum alloy A356–T6. Mater. Sci. Forum. Trans. Tech. Publ. (2007). https://doi.org/10.4028/www.scientific.net/MSF.546-549.989Article Google Scholar 
  17. N. Limodin, Application of X-ray microtomography to study the influence of the casting microstructure upon the tensile behaviour of an Al–Si alloy. Nucl. Instrum. Methods Phys. Res., Sect. B. 324, 57–62 (2014). https://doi.org/10.1016/j.nimb.2013.07.034
  18. R.Horváth, M. Réger, F. Oláh, Characterisation of defects in die cast aluminium parts, in IOP Conference Series: Materials Science and Engineering. 1246, No. 1, 012016, IOP Publishing, (2022). https://doi.org/10.1088/1757-899X/1246/1/012016
  19. A. Marin, What size of porosity can vacuum impregnation seal?, DIE CASTING ENGINEER, 16–18 (2019).
  20. J. Campbell, Complete casting handbook: metal casting processes, metallurgy, techniques and design. Butterworth-Heinemann. (2015)
  21. S. Lee, D. Han, S. Kang, N. Kim, Method of predicting shrinkage defects and deriving process conditions in HPDC (high-pressure die-casting) for electric vehicle motor housings. Int. J. Metalcast. (2023). https://doi.org/10.1007/s40962-023-01100-yArticle Google Scholar 
  22. N. Soga, A. Bandara, K. Kan, A. Koike, T. Aoki, Micro-computed tomography to analyze industrial die-cast Al-alloys and examine impregnation polymer resin as a casting cavity sealant. Prod. Eng. 15(6), 885–896 (2021). https://doi.org/10.1007/s11740-021-01071-1Article Google Scholar 
  23. G. Lloyd, Finding a solution to the eternal problem of porosity in casting. Die Casting Engineer. 40 (2012)
  24. H. Rottländer, W. Umrath, G. Voss, Fundamentals of leak detection. Leybold GMBH (ed) Cat, 199, 37. (2016)
  25. M. Réger, J. Gáti, F. Oláh, R. Horváth, E.R. Fábián, T. Bubonyi, Detection of porosity in impregnated die-cast aluminum alloy piece by metallography and computer tomography. Crystals 13(7), 1014 (2023). https://doi.org/10.3390/cryst13071014Article CAS Google Scholar 
  26. A. Marin, How to set up a vacuum impregnation sealant testing: improve part sealing with a disciplined testing approach. Die Casting Engineer. 10–13 (2021)
  27. T.V. Sai, T. Vinod, G. Sowmya, A critical review on casting types and defects. Eng. Technol. 3(2), 463–468 (2017)Google Scholar 
  28. T.T. Zhang, W.B. Yu, C.S. Ma, W.T. Chen, L. Zhang, S.M. Xiong, The effect of different high pressure die casting parameters on 3D microstructure and mechanical properties of AE44 magnesium alloy. J. Magnesium Alloys. (2022). https://doi.org/10.1016/j.jma.2022.05.001Article Google Scholar