Phase Field Simulation of Al–Fe–Mn–Si Quaternary Eutectic Solidification

This introductory paper is the research content of the paper ["Phase Field Simulation of Al–Fe–Mn–Si Quaternary Eutectic Solidification"] published by [MDPI].

1. Overview:

• Title: Phase Field Simulation of Al–Fe–Mn–Si Quaternary Eutectic Solidification
• Author: Kimiya NouraniNiaki, Murali Uddagiri, Daysianne Isidorio, Oleg Shchyglo, and Ingo Steinbach
• Publication Year: 2025
• Publishing Journal/Academic Society: Metals
• Keywords: aluminum; solidification; intermetallic; quaternary; multi-phase-field

2. Abstracts / Introduction

This study investigates the eutectic equilibrium phases in a multicomponent system through 3-D multi-phase-field simulations. Emphasizing the directional solidification process, the work examines the growth dynamics of intermetallic phase Al₁₃Fe₄, a lamellar structure (FCC-A1), and a quaternary phase beta-AlMnSi from the liquid that is solidified at a specific temperature. The eutectic transformation, described by the four phase reaction L → Al₁₃Fe₄ + FCC-A1 + beta-AlMnSi, is analyzed to develop a microstructure selection map. This map correlates stable growth modes with initial system composition and lamellar spacing. The results provide detailed insights into the segregation behaviour of alloying elements and their influence on transformation kinetics, enhancing the understanding of eutectic microstructure evolution in complex alloy systems.

3. Research Background:

Background of the Research Topic:

Aluminum alloys are extensively utilized in automotive, aerospace, and transportation industries due to their superior mechanical properties and sustainability potential. The increasing global emphasis on environmental sustainability and the rising demand for aluminum alloys can be effectively addressed by incorporating recycled aluminum alloys. This approach not only reduces production costs but also decreases energy consumption. Among commonly used aluminum alloys, the 3000 series is notable for its lightweight nature, high mechanical strength, and excellent formability [1]. Key alloying elements such as Fe, Mn, and Si play critical roles in enhancing these properties: Fe prevents mold sticking during die casting [2], Si improves liquid phase fluidity [3,4], and Mn stabilizes intermetallic phases [5,6], thereby improving mechanical properties. However, choosing the right composition of these elements is crucial, as exceeding their weight fractions can lead to the formation of brittle intermetallic compounds [7], adversely affecting mechanical performance. Therefore, effective control of phase formation is essential to optimize the mechanical properties of aluminum alloys during design and manufacturing [8-11].

Status of Existing Research:

To explore the large compositional space of multicomponent alloys, computational methods are employed to predict phase behavior under solidification and equilibrium conditions. Thermodynamic models are valuable tools for designing aluminum alloys [12,13]. The CALPHAD approach is widely used for material design and process optimization of aluminum alloys [1,14]. The strength of the CALPHAD method lies in its ability to use self-consistent parameters to predict thermodynamic behavior in multicomponent systems [8,15]. Phase field modeling is another computational approach that simulates complex systems, such as solidification [16], segregation [17-19], and grain growth [20], using thermodynamically grounded partial differential equations [21]. Accurately predicting changes in precipitate morphology, size, volume fraction, and spatial distribution during heat treatment is critical for understanding precipitate hardening effects. Meso-scale simulations, such as those for Al₂Cu precipitates, provide insights into these processes [22]. The phase field method, particularly with diffuse interface approaches, simplifies modeling by eliminating the need for explicit interface tracking [21]. Understanding and designing aluminum alloys through thermodynamic models is enhanced by numerical simulations. These models allow for the analysis of various factors influencing microstructural evolution [22-27]. However, evidence of distinct quaternary phases in aluminum alloys is limited. For instance, the α-AlMnSi phase extends significantly into the quaternary system, approaching the ternary Al-Fe-Si system, yet no stable quaternary phase exists in the aluminum-rich corner of the Al-Fe-Mn-Si system [28]. Combining computational thermodynamics with multi-phase-field models enables a detailed analysis of phase distributions in multicomponent systems. According to Warmuzek [29], rod-shaped FCC-A1 morphology can form through eutectic transformation involving two key reactions. However, experimental data on quaternary phases in multicomponent aluminum alloys remains scarce. Furthermore, Al₁₃Fe₄ is an important intermetallic phase in the Al–Fe–Mn–Si system because of its influence on the microstructure and properties of Al-based alloys. This phase is the only equilibrium phase forming in the Al–rich corner of the Al–Fe–Si system and it forms during solidification as part of eutectic reaction. This phase is especially common in recycled aluminum alloys, where iron tends to accumulate due to its low solubility in aluminum. As reported in Quan Li et al. [7], the Al₁₃Fe₄ intermetallic phase negatively impacts the mechanical properties of recycled aluminum alloys with high iron content by acting as a stress concentrator, reducing ductility and corrosion resistance [30]. Therefore, understanding the formation, morphology, and interactions of this phase with other intermetallics is essential for designing alloys that mitigate its detrimental effects [31]. Such research contributes to improving the structural performance, recyclability, and mechanical and corrosion-resistant properties of aluminum alloys [32].

Necessity of the Research:

The objective of this study is twofold: first, to develop a microstructural selection map of eutectic solid phases formed via key reactions leading to the emergence of the quaternary phase beta-AlMnSi; and second, to employ the phase field method to characterize the quaternary phase both qualitatively and quantitatively. This study focuses on the lamellar structure of FCC-A1, intermetallic precipitation, microstructural evolution, and the spatial distribution of beta-AlMnSi as the quaternary phase. These investigations, conducted through multi-phase-field simulations, aim to provide a comprehensive understanding of the mechanisms governing microstructure formation in complex eutectic systems.

4. Research Purpose and Research Questions:

Research Purpose:

The objective of this study is twofold: first, to develop a microstructural selection map of eutectic solid phases formed via key reactions leading to the emergence of the quaternary phase beta-AlMnSi; and second, to employ the phase field method to characterize the quaternary phase both qualitatively and quantitatively.

Key Research:

This study focuses on:

• the lamellar structure of FCC-A1,
• intermetallic precipitation,
• microstructural evolution, and
• the spatial distribution of beta-AlMnSi as the quaternary phase.
  These investigations, conducted through multi-phase-field simulations, aim to provide a comprehensive understanding of the mechanisms governing microstructure formation in complex eutectic systems.

5. Research Methodology

Research Design:

This study employs 3-D multi-phase-field simulations to investigate the eutectic equilibrium phases in a multicomponent system, emphasizing the directional solidification process. The model employed in this study is the multicomponent multi-phase-field (MPF) model developed by Steinbach and co-workers [21,46], implemented using the OpenPhase software version 4.7. For the simulation, a 3D box with dimensions of 60 × 60 × 120 grid cells and a grid resolution of 1 × 10⁻⁷ m was considered.

Data Collection Method:

The thermodynamic information is obtained from the COST-507 database using the CALPHAD method, implemented in Thermo-Calc software version 2021b. The system temperature is updated using the frozen temperature method, which accounts for a constant thermal gradient and cooling rate [47]. Nucleation was modeled based on AL Greer's approach [49,50], which relates the formation of nuclei to the local driving force exceeding the nucleation barrier.

Analysis Method:

The phase field approach [40] is a well-established numerical simulation technique used to model the microstructural evolution of materials during phase transformations. This method employs "diffuse interface models” to resolve interactions between phases. The multi-phase-field (MPF) model incorporates a diffusion equation to represent the evolution of solute composition across phases. Thermodynamic minimization is essential for determining phase concentrations based on the mixture concentration and individual phase fractions derived from the phase fields.

Research Subjects and Scope:

The nominal composition of the quaternary Al-Fe-Mn-Si system, as presented in Table 3, is derived from the experimental reference [51]. The simulation domain is restricted to the scale of multiple dendrite growth within a single grain due to the limited size of the simulation box. The study focuses on the four phase reaction L → Al₁₃Fe₄ + FCC-A1 + beta-AlMnSi.

6. Main Research Results:

Key Research Results:

• The simulation results indicate that, for the selected alloy system, solidification begins with the nucleation and growth of the spherical eutectic phase Al₁₃Fe₄ throughout the liquid.
• As solidification progresses and the system temperature decreases, the primary eutectic FCC-A1 phase forms along the growth direction.
• Subsequently, supersaturation of the remaining liquid leads to the nucleation of the quaternary beta-AlMnSi phase.
• The volume fractions of these phases, as obtained from the simulation results, closely align with the thermodynamic calculations performed using the open database for the Al-Fe-Mn-Si system.
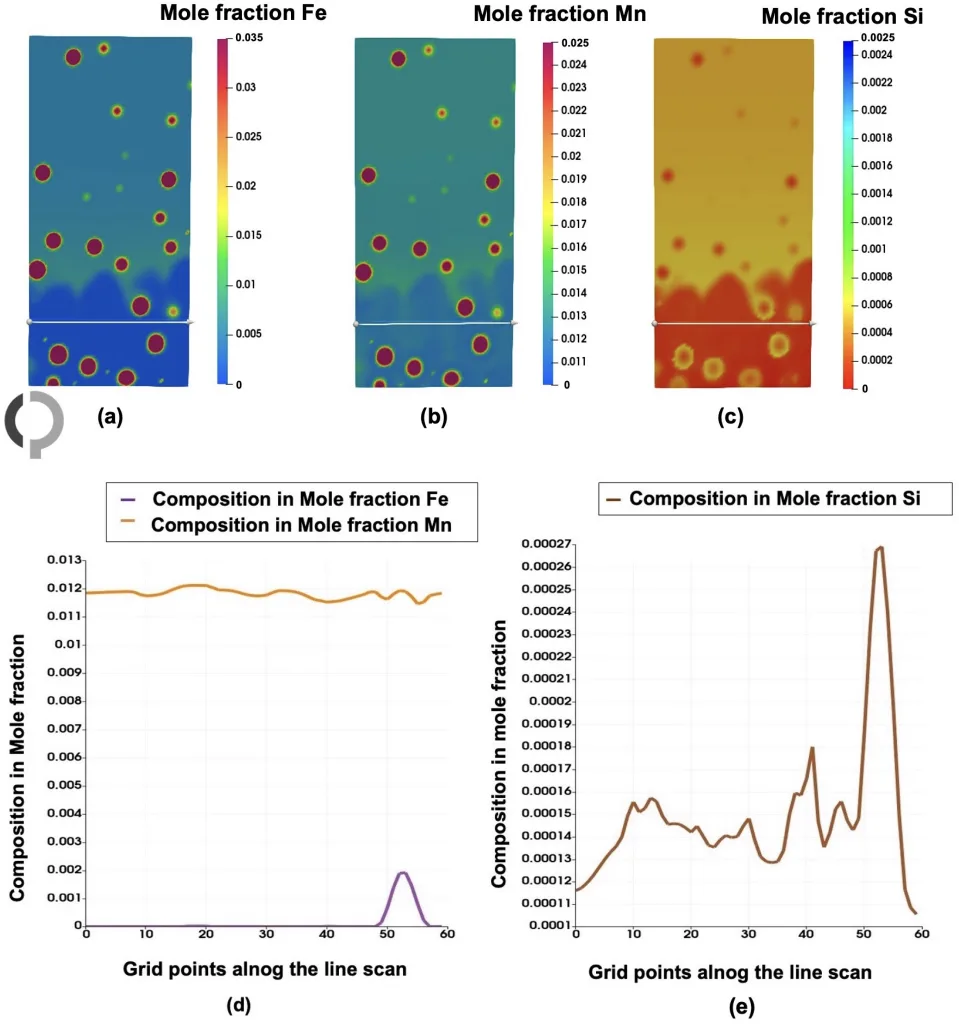
• Elemental distribution analysis reveals significant variations in the segregation behavior of alloying elements in the Al-Fe-Mn-Si system.
• The elements Fe and Mn are primarily associated with the formation of the Al₁₃Fe₄ phase, while silicon (Si) is predominantly found in the primary eutectic FCC-A1 phase.
• The diffusivity of Mn and Si, acting as stabilizers in the quaternary beta-AlMnSi phase, exhibits an upward trend in concentration.
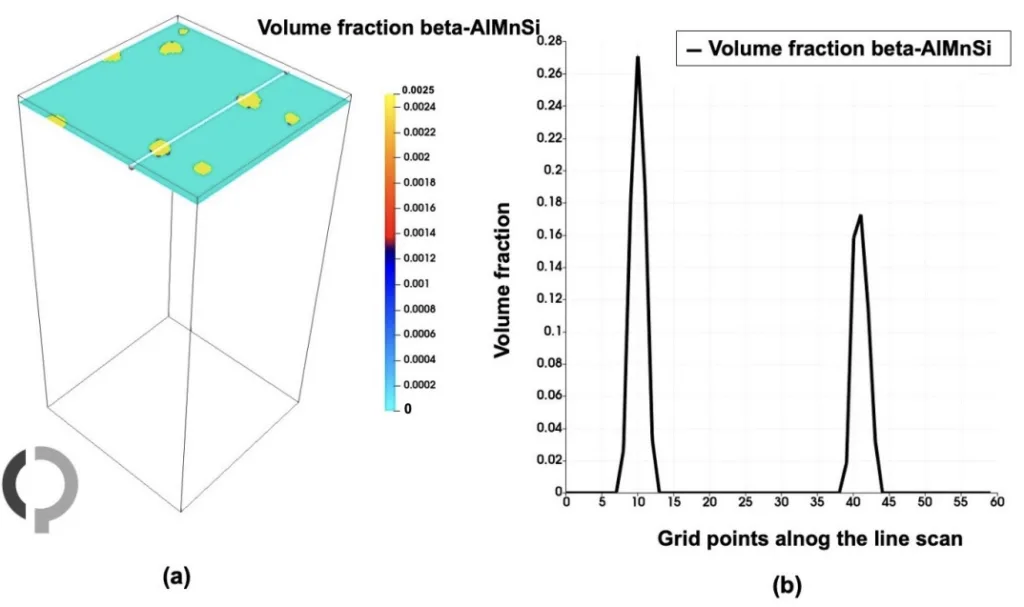
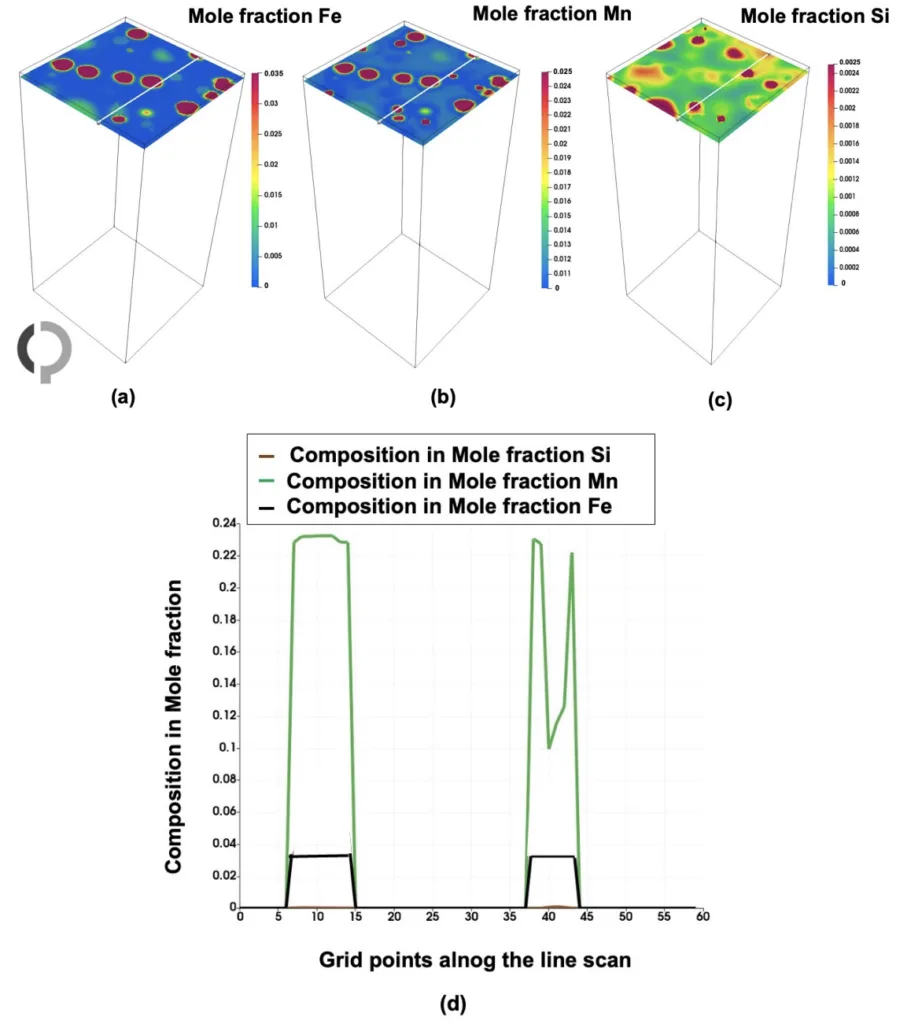
• The analysis of line scans at the eutectic phases reveals the distinct segregation behavior of Fe in the beta-AlMnSi phase. Initially, Fe exhibits a higher level of segregation into the liquid phase, which subsequently decreases as the liquid transforms into the quaternary beta-AlMnSi phase. A noticeable depletion of Fe is observed in this phase.

Analysis of presented data:

• Formation of Intermetallic Phases: The simulation successfully captured the sequential formation of Al₁₃Fe₄, FCC-A1, and beta-AlMnSi phases during eutectic solidification. The Al₁₃Fe₄ phase nucleates first, followed by FCC-A1, and finally beta-AlMnSi in the remaining liquid.
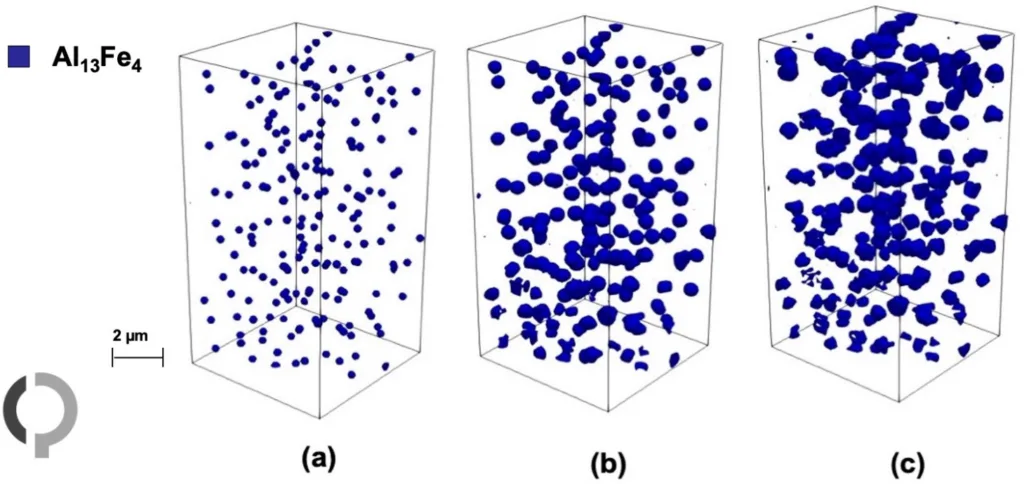
• Microstructure Evolution: The 3D phase-field simulation effectively visualizes the microstructure evolution, showing the spatial distribution and interactions of the different phases. The FCC-A1 phase forms a lamellar or rod-shaped eutectic structure.
• Elemental Segregation: The simulation reveals significant segregation of alloying elements. Fe and Mn are enriched in the Al₁₃Fe₄ phase, while Si is more concentrated in the FCC-A1 phase. Beta-AlMnSi phase shows Mn and Si enrichment and Fe depletion.
• Phase Volume Fractions: The volume fractions of the phases obtained from the simulation are consistent with thermodynamic calculations using the COST-507 database and Thermo-Calc software.

Figure Name List:

• Figure 1. (a) Liquidus projection of the Al-Fe-Si ternary system and (b) Al-Mn-Si ternary system [28].
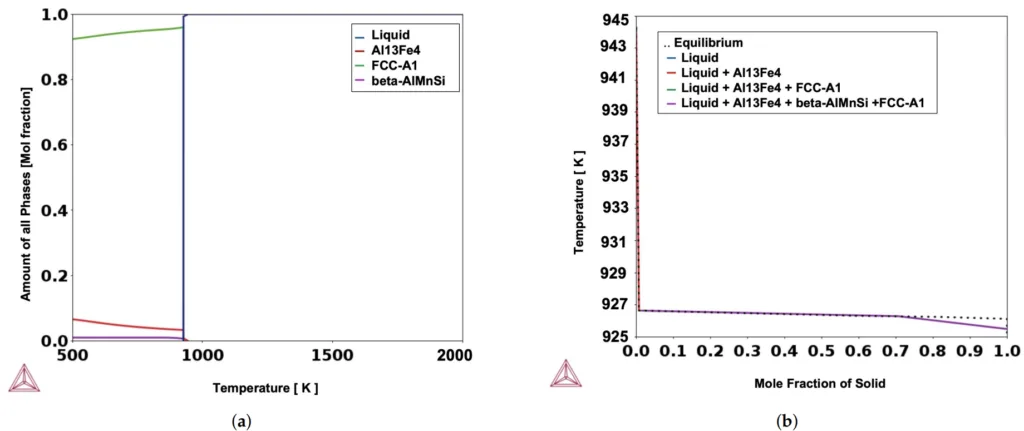
• Figure 2. Calculation of stable phase fractions: (a) under equilibrium conditions as a function of temperature based on the element percentages in Table 3, and (b) using Scheil-Gulliver solidification based on the element contents in Table 3.
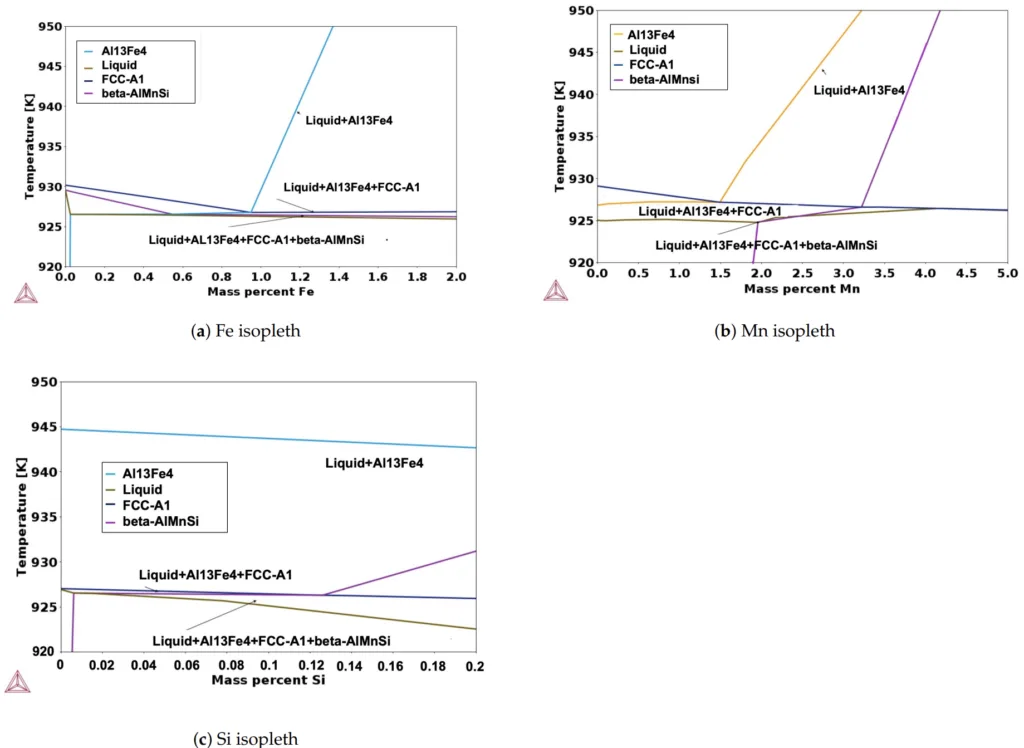
• Figure 3. The isopleth phase diagrams (a−c) show the nucleation and growth of FCC-A1, Al₁₃Fe₄, and fi-AlMnSi from the undercooled liquid. The X-axis represents the chemical composition of (a) Fe, (b) Mn, and (c) Si with respect to temperature.
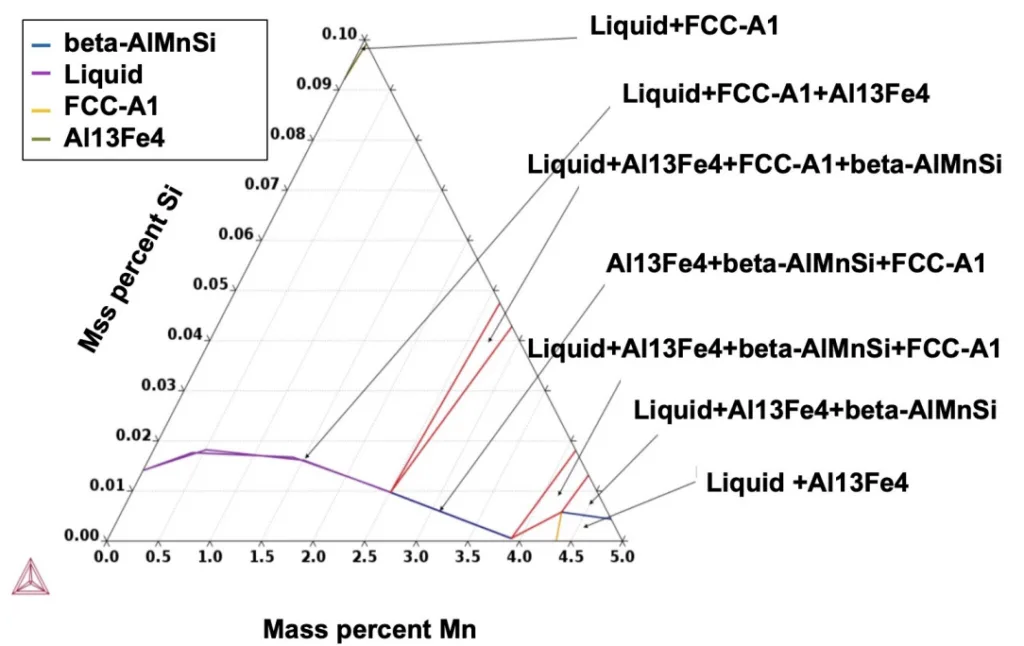
• Figure 4. FCC-A1, Al₁₃Fe₄ and beta-AlMnSi with liquid in alloy Al-Fe-Mn-Si system while Mn and Si elements are on the triangle sides in the rich corner aluminum.
• Figure 5. (a) Nucleation of Al₁₃Fe₄ at t₀ = 0.0195 s, (b) growth of this precipitate at t₁ = 0.031 s, (c) completion of the precipitate at t₂ = 0.052 s.
• Figure 6. (a) Nucleation of FCC-A1 at t₀ = 0.0255 s, (b) growth of this phase at t₁ = 0.031 s, and (c) completion of the solid phase at t₂ = 0.052 s.
• Figure 7. (a) Nucleation of beta-AlMnSi at t₀ = 0.039 s, (b) t₁ = 0.04 s growth of this phase at, and (c) completion of the phase at t₂ = 0.052 s.
• Figure 8. Microstructure evolution of the multicomponent Al-Fe-Mn-Si system during directional solidification via eutectic reactions at four different time steps: (a) t₀ = 0.0255 s, (b) t₁ = 0.032 s, (c) t₂ = 0.039 s and (d) t₃ = 0.052 s, showing the phase fractions of Al₁₃Fe₄ (dark blue), FCC-A1 (light blue), and beta-AlMnSi (orange) in the multi-phase-field simulation.
• Figure 9. Concentration distribution of all solute components in the multicomponent Al-Fe-Mn-Si system (a) Fe, (b) Mn, (c) Si at t = 0.04 s. (d) the morphology with phase information is shown on the right).
• Figure 10. (a) Line scan of the volume fraction of Al₁₃Fe₄ along the white line. (b) Depicts the volume fractions of Al₁₃Fe₄ and the liquid phase.
• Figure 11. Line scan of solute elements in the Al-Fe-Mn-Si system at a specific time step along the Al₁₃Fe₄ and liquid phases (shown by the white line). (a−c) Show the mole fractions of Fe, Mn, and Si, respectively. (d,e) highlights the phases presence, where Fe and Mn segregated, while Si is depleted.
• Figure 12. (a) Line scan of the volume fraction of liquid along the white line. (b) Shows the volume fractions of FCC-A1 and the liquid phase.
• Figure 13. Line scan of solute elements in the Al-Fe-Mn-Si system at a specific time step along the FCC-A1 and liquid phases (shown by the white line). (a−c) Show the mole fractions of Fe, Mn, and Si, respectively. (d,e) highlights the phases presence, where Fe and Mn depleted, while Si is segregated.
• Figure 14. (a) Line scan of the volume fraction of beta-AlMnSi (shown by white line). (b) Shows the volume fractions of beta-AlMnSi phase.
• Figure 15. Line scan of solute elements in the Al-Fe-Mn-Si system at a specific time step along the beta-AlMnSi phase (indicated by the white line). (a−c) Show the mole fractions of Fe, Mn, and Si, respectively. (d) Highlights the phase presence, where Fe is depleted, while Si and Mn are segregated.

7. Conclusion:

Summary of Key Findings:

The eutectic solidification morphology of the multicomponent Al-Fe-Mn-Si system under directional solidification conditions is investigated using a multi-phase-field model coupled with a CALPHAD thermodynamic database. The 3D microstructure selection map reveals the formation of three distinct solid phases: intermetallic Al₁₃Fe₄, primary eutectic FCC-A1, and quaternary beta-AlMnSi. Solidification starts with Al₁₃Fe₄ nucleation, followed by FCC-A1 growth, and finally beta-AlMnSi nucleation in the supersaturated liquid. Elemental distribution analysis shows Fe and Mn segregation in Al₁₃Fe₄, Si in FCC-A1, and Mn and Si enrichment with Fe depletion in beta-AlMnSi. Line scans confirm Fe depletion in beta-AlMnSi and distinct segregation behaviors of Fe, Mn, and Si across different phases.

Academic Significance of the Study:

This research provides a detailed understanding of the eutectic solidification process in a complex quaternary Al-Fe-Mn-Si alloy system using advanced phase-field simulations. The study successfully demonstrates the capability of the multi-phase-field model, coupled with CALPHAD database, to predict and analyze the microstructure evolution and elemental segregation in multicomponent alloys. The findings enhance the fundamental knowledge of phase transformations and solidification kinetics in complex alloy systems, particularly concerning the formation of quaternary phases.

Practical Implications:

The developed microstructure selection map and the insights into phase formation and elemental segregation can be utilized for optimizing the design and processing of Al-Fe-Mn-Si alloys. Understanding the role of each alloying element and the sequence of phase formation can aid in controlling the microstructure and improving the mechanical properties of die-cast aluminum alloys. This is particularly relevant for recycled aluminum alloys where iron is a common impurity, and the formation of intermetallic phases like Al₁₃Fe₄ significantly impacts performance. The study provides a computational tool and knowledge base for alloy designers and process engineers in the die casting industry.

Limitations of the Study and Areas for Future Research:

Further research is required to quantify the influence of interface anisotropies across various phases. Additionally, the simulations in this study were designed with reference to both experimental data and thermodynamic modeling results. However, the obtained simulation results require direct validation through experimental studies conducted on the same alloy composition. Future work could focus on experimental validation of the simulation results and further refinement of the model by incorporating interface anisotropies and more detailed kinetic data. Investigating a wider range of alloy compositions and solidification conditions would also be beneficial.

8. References:

• [1] Chen, H.L.; Chen, Q.; Engström, A. Development and applications of the TCAL aluminum alloy database. Calphad 2018, 62, 154-171.
• [2] Otani, L.B.; Soyama, J.; Zepon, G.; Costa e Silva, A.; Kiminami, C.S.; Botta, W.J.; Bolfarini, C. Predicting the formation of intermetallic phases in the Al-Si-Fe system with Mn additions. J. Phase Equilibria Diffus. 2017, 38, 298-304.
• [3] Zolotorevsky, V.S.; Belov, N.A.; Glazoff, M.V. Casting Aluminum Alloys; Elsevier: Amsterdam, The Netherlands, 2007; Volume 12.
• [4] Callegari, B.; Lima, T.N.; Coelho, R.S. The influence of alloying elements on the microstructure and properties of Al-Si-based casting alloys: A review. Metals 2023, 13, 1174.
• [5] Tian, N.; Wang, G.; Zhou, Y.; Liu, C.; Liu, K.; Zhao, G.; Zuo, L. Phase Formation and Microstructure Evolution of Al-5Si-0.8 Mg Alloys with Different Mn Concentrations. Metals 2021, 11, 308.
• [6] Zhenjie, C.; Haichang, J.; Duo, Z.; Qijuan, D.; Junjun, P.; Luanluan, J. Influence of Mn on the precipitates in 6082 aluminum alloy. J. Mater. Sci. 2024, 59, 9734-9748.
• [7] Li, Q.; Wang, J.; Xue, C.; Wang, S.; Yang, X.; Tian, G.; Su, H.; Li, X.; Miao, Y. Transforming detrimental intermetallics by accumulative thermal and strain energies in the Al-Fe-Si alloy. J. Mater. Sci. 2024, 59, 1699–1720.
• [8] Moore, E.; Turchi, P.; Lordi, V.; Weiss, D.; Sims, Z.; Henderson, H.; Kesler, M.; Rios, O.; McCall, S.; Perron, A. Thermodynamic Modeling of the Al-Ce-Cu-Mg-Si System and Its Application to Aluminum-Cerium Alloy Design. J. Phase Equilibria Diffus. 2020, 41, 764-783.
• [9] Liu, G.; Müller, D.B. Addressing sustainability in the aluminum industry: A critical review of life cycle assessments. J. Clean. Prod. 2012, 35, 108-117.
• [10] Shabestari, S. The effect of iron and manganese on the formation of intermetallic compounds in aluminum-silicon alloys. Mater. Sci. Eng. A 2004, 383, 289–298.
• [11] Wang, E.; Hui, X.; Chen, G. Eutectic Al-Si-Cu-Fe-Mn alloys with enhanced mechanical properties at room and elevated temperature. Mater. Des. 2011, 32, 4333-4340.
• [12] Liu, C.; Garner, A.; Zhao, H.; Prangnell, P.B.; Gault, B.; Raabe, D.; Shanthraj, P. CALPHAD-informed phase-field modeling of grain boundary microchemistry and precipitation in Al-Zn-Mg-Cu alloys. Acta Mater. 2021, 214, 116966.
• [13] Liu, C.; Davis, A.; Fellowes, J.; Prangnell, P.B.; Raabe, D.; Shanthraj, P. CALPHAD-informed phase-field model for two-sublattice phases based on chemical potentials: η-phase precipitation in Al-Zn-Mg-Cu alloys. Acta Mater. 2022, 226, 117602.
• [14] Zhang, F.; Liang, S.; Zhang, C.; Chen, S.; Lv, D.; Cao, W.; Kou, S. Prediction of cracking susceptibility of commercial aluminum alloys during solidification. Metals 2021, 11, 1479.
• [15] Jha, R.; Dulikravich, G.S. Temperature Regimes and Chemistry for Stabilizing Precipitation Hardening Phases in Al-Sc Alloys: Combined CALPHAD-Deep Machine Learning. ASME Open J. Eng. 2022, 1. spanning 12 pages.
• [16] Jreidini, P.; Pinomaa, T.; Wiezorek, J.M.; McKeown, J.T.; Laukkanen, A.; Provatas, N. Orientation gradients in rapidly solidified pure aluminum thin films: comparison of experiments and phase-field crystal simulations. Phys. Rev. Lett. 2021, 127, 205701.
• [17] Chen, J.; Guo, M.; Yang, M.; Cui, T.; Cui, B.; Zhang, J. Insight into element segregation mechanisms during creep in γ'-strengthened Co-based superalloy by elastoplastic phase-field simulation. Prog. Nat. Sci. Mater. Int. 2024, 34, 873–879.
• [18] Liu, X.; Shen, W.; Liu, W. Phase-Field Simulation of Precipitation and Grain Boundary Segregation in Fe-Cr-Al Alloys under Irradiation. Nanomaterials 2024, 14, 1198.
• [19] Gong, T.Z.; Chen, Y.; Hao, W.Y.; Chen, X.Q.; Li, D.Z. Modeling segregation of Fe-C alloy in solidification by phase-field method coupled with thermodynamics. Metals 2023, 13, 1148.
• [20] Staublin, P.; Mukherjee, A.; Warren, J.A.; Voorhees, P.W. Phase-field model for anisotropic grain growth. Acta Mater. 2022, 237, 118169.
• [21] Steinbach, I. Phase-field models in materials science. Model. Simul. Mater. Sci. Eng. 2009, 17, 073001.
• [22] Ji, Y.; Ghaffari, B.; Li, M.; Chen, L.Q. Phase-field modeling of e' precipitation kinetics in 319 aluminum alloys. Comput. Mater. Sci. 2018, 151, 84-94.
• [23] Provatas, N.; Elder, K. Phase-Field Methods in Materials Science and Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2011.
• [24] Jokisaari, A.M.; Voorhees, P.W.; Guyer, J.E.; Warren, J.A.; Heinonen, O.G. Phase field benchmark problems for dendritic growth and linear elasticity. Comput. Mater. Sci. 2018, 149, 336-347.
• [25] Biswas, S.; Schwen, D.; Singh, J.; Tomar, V. A study of the evolution of microstructure and consolidation kinetics during sintering using a phase field modeling based approach. Extrem. Mech. Lett. 2016, 7, 78–89.
• [26] Biswas, S.; Schwen, D.; Tomar, V. Implementation of a phase field model for simulating evolution of two powder particles representing microstructural changes during sintering. J. Mater. Sci. 2018, 53, 5799–5825.
• [27] Militzer, M. Phase field modeling of microstructure evolution in steels. Curr. Opin. Solid State Mater. Sci. 2011, 15, 106–115.
• [28] Lacaze, J.; Eleno, L.; Sundman, B. Thermodynamic assessment of the aluminum corner of the Al-Fe-Mn-Si system. Metall. Mater. Trans. A 2010, 41, 2208-2215.
• [29] Warmuzek, M.; Ratuszek, W.; Sęk-Sas, G. Chemical inhomogeneity of intermetallic phases precipitates formed during solidification of Al-Si alloys. Mater. Charact. 2005, 54, 31-40.
• [30] Allen, C.; O'reilly, K.; Cantor, B.; Evans, P. Intermetallic phase selection in 1XXX Al alloys. Prog. Mater. Sci. 1998, 43, 89–170.
• [31] Arbeiter, J.; Vončina, M.; Volšak, D.; Medved, J. Evolution of Fe-based intermetallic phases during homogenization of Al-Fe hypoeutectic alloy. J. Therm. Anal. Calorim. 2020, 142, 1693–1699.
• [32] Wang, X.; Guan, R.; Misra, R.; Wang, Y.; Li, H.; Shang, Y. The mechanistic contribution of nanosized Al3Fe phase on the mechanical properties of Al-Fe alloy. Mater. Sci. Eng. A 2018, 724, 452-460.
• [33] Ansara, I.; Dinsdale, A.; Rand, M. Thermochemical Database for Light Metal Alloys; Office for Official Publications of the European Communities: Luxembourg, 1998.
• [34] Eleno, L.; Vezelỳ, J.; Sundman, B.; Cieslar, M.; Lacaze, J. Assessment of the Al corner of the ternary Al-Fe-Si system. Mater. Sci. Forum 2010, 649, 523-528.
• [35] Zakharov, A.; Guldin, I.; Arnold, A. Phase Diagram of the Al-Si-Fe-Mn System in the 10-14% Si, 0-3% Fe, and 0-4% Mn Concentration Ranges. (Translation). Russ. Metall. 1989, 209-213. Issue 4.
• [36] Flores-V, A.; Sukiennik, M.; Castillejos-E, A.; Acosta-G, F.; Escobedo-B, J. A kinetic study on the nucleation and growth of the Al8FeMnSi2 intermetallic compound for aluminum scrap purification. Intermetallics 1998, 6, 217-227.
• [37] Onderka, B.; Sukiennik, M.; Fitzner, K. Determination of the stability of Al11. 8FeMn1. 6Si1. 6 phase existing in the quaternary Al-Fe-Mn-Si system. Arch. Metall. 2000, 45, 119–132.
• [38] Munson, D. A clarification of the phases occurring in aluminium-rich aluminium-iron-silicon alloys, with particular reference to the ternary phase alpha-AlFeSi. Inst. Met. J. 1967, 95, 217–219.
• [39] Tibballs, J.; Horst, J.; Simensen, C. Precipitation of a-Al (Fe, Mn) Si from the melt. J. Mater. Sci. 2001, 36, 937–941.
• [40] Steinbach, I.; Pezzolla, F.; Nestler, B.; Seeßelberg, M.; Prieler, R.; Schmitz, G.J.; Rezende, J.L. A phase field concept for multiphase systems. Phys. D Nonlinear Phenom. 1996, 94, 135-147.
• [41] Uddagiri, M.; Shchyglo, O.; Steinbach, I.; Tegeler, M. Solidification of the Ni-based superalloy CMSX-4 simulated with full complexity in 3-dimensions. Prog. Addit. Manuf. 2023, 1-12.
• [42] Wang, Z.; Liang, C.; Wang, D.; Yue, X.; Li, J.; Ding, X. Unveiling the Co effect on the temporal evolution kinetics of γ' phase in Ni-Al-Co model superalloys via CALPHAD-informed phase field simulations. Acta Mater. 2023, 258, 119247.
• [43] Wang, Z.; Liang, C.; Wang, D.; Ding, X. Uncovering the effect of Mo addition on the precipitation kinetics of the y' phase in Ni-Al-Mo model superalloys using CALPHAD-assisted phase-field simulations. J. Mater. Sci. 2024, 1–20.
• [44] Thakur, A.K.; Kovacevic, S.; Manga, V.R.; Deymier, P.A.; Muralidharan, K. A first-principles and CALPHAD-assisted phase-field model for microstructure evolution: Application to Mo-V binary alloy systems. Mater. Des. 2023, 235, 112443.
• [45] Warnken, N.; Ma, D.; Drevermann, A.; Reed, R.C.; Fries, S.; Steinbach, I. Phase-field modelling of as-cast microstructure evolution in nickel-based superalloys. Acta Mater. 2009, 57, 5862-5875.
• [46] Steinbach, I.; Böttger, B.; Eiken, J.; Warnken, N.; Fries, S. CALPHAD and phase-field modeling: A successful liaison. J. Phase Equilibria Diffus. 2007, 28, 101–106.
• [47] Keller, T.; Lindwall, G.; Ghosh, S.; Ma, L.; Lane, B.M.; Zhang, F.; Kattner, U.R.; Lass, E.A.; Heigel, J.C.; Idell, Y.; et al. Application of finite element, phase-field, and CALPHAD-based methods to additive manufacturing of Ni-based superalloys. Acta Mater. 2017, 139, 244-253.
• [48] Tegeler, M.; Shchyglo, O.; Kamachali, R.D.; Monas, A.; Steinbach, I.; Sutmann, G. Parallel multiphase field simulations with OpenPhase. Comput. Phys. Commun. 2017, 215, 173–187.
• [49] Greer, A. Overview: Application of heterogeneous nucleation in grain-refining of metals. J. Chem. Phys. 2016, 145.
• [50] Uddagiri, M.; Shchyglo, O.; Steinbach, I.; Wahlmann, B.; Koerner, C. Phase-field study of the history-effect of remelted microstructures on nucleation during additive manufacturing of ni-based superalloys. Metall. Mater. Trans. A 2023, 54, 1825-1842.
• [51] Park, J.; Oh, C.S.; Kang, J.H.; Jung, J.G.; Lee, J.M. Solidification and Precipitation Microstructure Simulation of a Hypereutectic Al-Mn-Fe-Si Alloy in Semi-Quantitative Phase-Field Modeling with Experimental Aid. Metals 2020, 10, 1325.
• [52] Hallstedt, B.; Khvan, A.V.; Lindahl, B.B.; Selleby, M.; Liu, S. PrecHiMn-4-A thermodynamic database for high-Mn steels. Calphad 2017, 56, 49-57.
• [53] Michael, K.; Philipp, S.; Britta, N.; et al. Applications of the phase-field method for the solidification of microstructures in multi-component systems. J. Indian Inst. Sci. 2016, 96, 235-256.
• [54] Thesis, D. Characterization of equilibrium phases in 8xxx alloys for the optimization of the thermodynamic database for MatCalc. Ph.D. Thesis, Technische Universität Wien, Vienna, Austria, 2022.
• [55] Que, Z.; Fang, C.; Mendis, C.L.; Wang, Y.; Fan, Z. Effects of Si solution in 0-A113Fe4 on phase transformation between Fe-containing intermetallic compounds in Al alloys. J. Alloy. Compd. 2023, 932, 167587.
• [56] Yan, X.; Ding, L.; Chen, S.; Xie, F.; Chu, M.; Chang, Y.A. Predicting microstructure and microsegregation in multicomponent aluminum alloys. In Essential Readings in Light Metals: Volume 3 Cast Shop for Aluminum Production; Springer: Berlin/Heidelberg, Germany, 2016; pp. 512–518.

9. Copyright:

• This material is "Kimiya NouraniNiaki"'s paper: Based on "Phase Field Simulation of Al–Fe–Mn–Si Quaternary Eutectic Solidification".
• Paper Source: https://doi.org/10.3390/met15020135

This material was created to introduce the above paper, and unauthorized use for commercial purposes is prohibited.
Copyright © 2025 CASTMAN. All rights reserved.