J Ou1, C Wei1,2, D Maijer1, S Cockcroft1, L A2, Y Zhang2, Z Chen2 and Z Zhu2
Published under licence by IOP Publishing Ltd
IOP Conference Series: Materials Science and Engineering, Volume 861, MCWASP XV: International Conference on Modelling of Casting, Welding and Advanced Solidification Processes 22-23 June 2020, Jönköping, Sweden
Citation J Ou et al 2020 IOP Conf. Ser.: Mater. Sci. Eng. 861 012030
Abstract
Die (permanent) casting is one of the major manufacturing processes for aluminum automotive parts thanks to its ability to provide a good balance between mechanical performance and production efficiency. In the die casting industry, computational modelling has been widely adopted to analyze, troubleshoot and optimize die design and process parameters. In this work, a computational modelling methodology including key process boundary conditions and material properties has been developed to simulate an industrial die casting process of an aluminum automotive part. It has been demonstrated that the model is accurate and robust with respect to temperature and defect prediction by comparison with a large amount of high-quality plant-trial data. The data was acquired from an in-house designed data acquisition system (DAQ) connected to an instrumented die and industrial production equipment in a production facility.
Introduction
For the industrial applications, assessing a computational model’s accuracy is often limited by the availability of high-quality, widespread data from the production line which can be challenging to acquire due to technical barriers and cost. Another challenge is that models are often inaccurate because of insufficient understanding and description of the complex physical phenomena that occur during the casting processes. This is exacerbated when the process conditions and die structure are significantly different from past experience. This study seeks to apply the modelling methodology that was originally developed for an LPDC wheel production process to a novel Counter Pressure Casting process for an automotive control arm. The LPDC modelling methodology being applied here has been refined over the last 20 years and incorporates relevant material properties and boundary/interface conditions that have been characterized by measurements on the lab- and industrial-scale and/or augmented with data collected from literature. The methodology has been validated for a range of process conditions and die structures. The CPC process has similar operation principles and employs a permanent die like the LPDC, with unique features – refer to the CPC Process Description section later for more details.
Quantitative temperature data has been acquired from an industrial CPC process to validate the model. This work will present an assessment of the accuracy and robustness of the modelling methodology as applied to the CPC process, and provide insights into the comparison of the CPC and LPDC processes from the modelling perspective. Note: since this is part of an applied research project with an industrial partner, confidential process information must be protected and will not be presented in this manuscript.
In the auto industry, the trend continues towards increased usage of aluminum automotive parts produced by permanent die casting processes thanks to its lightweight, relatively low cost and good mechanical performance. Die casting processes have become very sophisticated to improve quality, however, various types of casting-related defects continue to challenge production engineers. For example, the large-scale (normally >1 mm) irregular shape porosity may be caused by large liquid encapsulation when directional solidification is not achieved. Small-scale (normally <1 mm) roundshape porosity may also form due to the reduction of hydrogen solubility associated with the liquid to solid phase transformation. Oxide film entrapment may occur during filling when the free surface of liquid aluminum is disturbed because of turbulence.
As a complement to experience-based design, numerical simulations have been adopted to provide insights and guidance to the design activities for dies and process operation in the casting industry. It has successfully helped to reduce the risk of critical defect formation. However, in industry, there is still a strong desire to improve model accuracy and robustness in order to expand their use. This requires a systematic evaluation and characterization of the relevant physics, e.g. material properties and key boundary/interface conditions associated with interface behavior and cooling. The transport phenomena and the relevant boundary conditions are often complicated and have been investigated by a numerous researchers. Examples include the studies carried out by Nishida et al. [1] and Wei et al. [2] for the investigation of the die/casting interface behavior and the associated heat transfer. Moayedinia et al. [3] and Hu et al. [4] conducted work to characterize the heat transfer of water cooling in die cooling channels. Drawing on this body of fundamental work, researchers have been able to develop computational models of casting processes with improved accuracy. For example, Zhang et al. [5] developed a 3D thermal model of the low pressure die casting (LPDC) of A356 aluminum alloys wheels using ABAQUS. It correlated well to measured data with respect to die temperature and shrinkage-based porosity.
CPC process description
The CPC process is a relatively new casting process that can be used to produce aluminum automotive parts. There is less known about this process in the casting industry compared to the conventional LPDC process. In principle, CPC process operation is similar to the LPDC process. The major difference is that the die is placed in a controlled pressure chamber in the CPC process. This allows the pressure in the chamber to be increased during both the filling and solidification stages. For a detailed introduction to the CPC process, readers are referred to the manuscript titled “Toward the Development of a ThermalStress Model of an Industrial Counter Pressure Casting Process” submitted by Chunying Wei in the
proceedings of this conference.
As the CPC process allows the filling and solidification stages to occur under a higher pressure over the LPDC process, it has been argued that it benefits the casting quality in several ways [6]: 1) low oxide film entrainment because of reduce free surface turbulence; 2) refined microstructure due to enhanced cooling rate caused by improved die/casting interfacial heat transfer; and 3) reduced number and/or size of shrinkage-based porosity from solidification at relatively high counter pressure. At present there is little practical evidence to support these assertions.
Model development
The model was developed using the Finite Element Method (FEM) based, commercial software package, ProCAST™. It is able to simulate various casting processes and is capable of describing the transport phenomena occurring in the different stages of casting, i.e. filling (fluid flow), solidification, die opening, part ejection and die closing. It should be noted that the solution of the fluid flow (momentum conservation via the Navier-Stoke Equations) is only activated in the filling stages to improve computational efficiency. Whereas, the energy conservation is always computed throughout the process to update temperature distributions in the casting and die.
In addition, it should be noted that the modelling methodology was originally developed for the LPDC process. There are a number of parameters that common to both processes, such as the need to turn cooling on/off with specific timing, die manipulation timings and pressure curves, that are implemented in a similar manner or are based on calculation. One significant except is the heat flux representing die cooling because of residual water in the cooling manifolds - introduced in detail below.
Please note that the cooling configuration in the CPC process is different from that in the LPDC process in terms of the physical structure and layout.
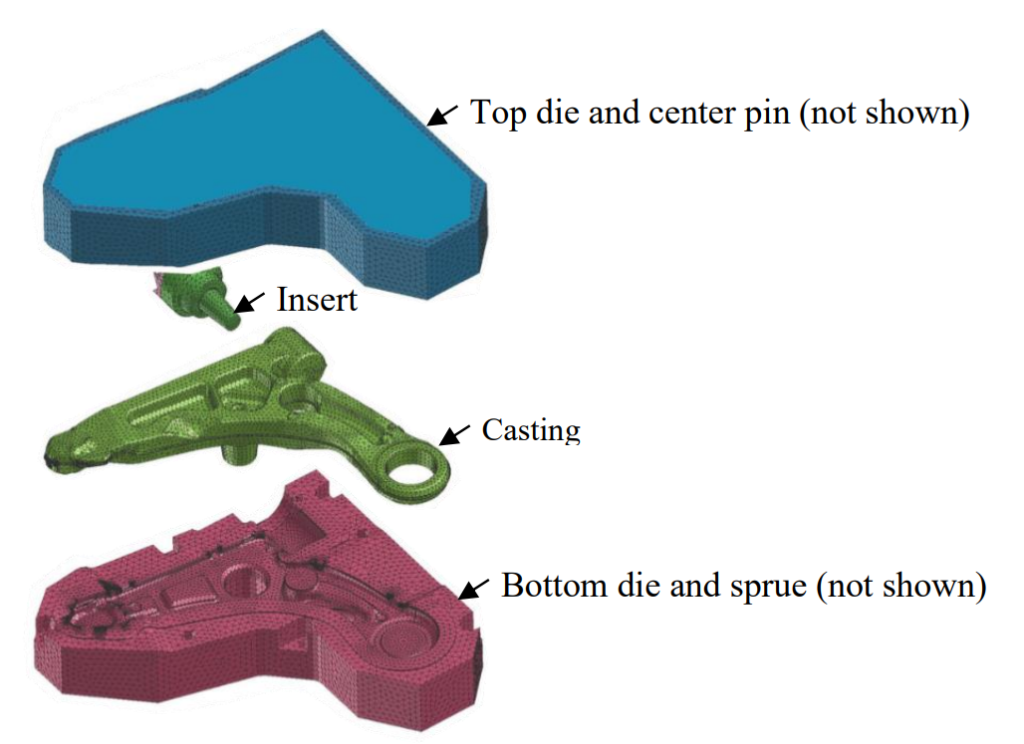
3.1. Geometry and mesh
Figure 1 shows the geometry and mesh of the control arm casting and die / insert sections included in the model. The top surface of the top die is obscured to hide the detailed design of cooling configuration due to confidentiality. The mesh was generated using the following approach:
• The casting and the die/casting interface were meshed with a relatively fine size – 4~6 mm;
• At the locations where strong heat transfer exists, i.e. in proximity to the die cooling locations, a mesh size of 2 mm was selected;
• The mesh size was increased gradually moving away from the die/casting interface; and
• A maximum mesh size of 10 mm was used for the balance of the die structure
After applying the above, the resulting mesh has 73,996 surface cells and 448,137 body cells.
3.2. Part materials and thermo-physical properties
The materials used are listed in table 1. Due to space limitation, the thermo-physical properties have been omitted from this paper, but they are based on those found in the references [5] and [7]. Table 1. Parts and their materials Part Material Die structure (top and bottom dies, and the insert) H13 Casting A356
3.3. Initial conditions
At the start of a casting cycle, the die does not contain liquid metal and only the initial temperature needs to be specified. The CPC process is a cyclic process where the temperature of the die after each casting cycle becomes the initial temperature condition for the start of the next cycle. If there are no process condition changes, eventually the process will reach cyclic steady-state where the temperature distribution at the start and end of each cycle is the same. The initial condition does not impact the final
3.3. Initial conditions
At the start of a casting cycle, the die does not contain liquid metal and only the initial temperature needs to be specified. The CPC process is a cyclic process where the temperature of the die after each casting cycle becomes the initial temperature condition for the start of the next cycle. If there are no process condition changes, eventually the process will reach cyclic steady-state where the temperature distribution at the start and end of each cycle is the same. The initial condition does not impact the final temperature distribution at cyclic steady-state. However, the number of cycles required to reach steadystate will vary depending on the initial conditions. In this work, the temperature field calculated from the previous run was employed as the initial condition. This approach significantly reduces the number of cycles required to reach steady state compared to using a uniform temperature for the initial conditions.
3.4. Boundary conditions
Two categories of boundary conditions, i.e. thermal and fluid flow boundary conditions, are required to solve the energy conservation equationsfor temperature and momentum conservation equations for fluid flow, respectively. As noted earlier, fluid flow was only solved for in the casting domain during the filling stage.
3.4.1. Thermal boundary conditions. Water cooling - water cooling is used to rapidly extract heat from
the die, and therefore, it is one of the most important process parameters for the process control. The water cooling configurations are carefully designed with respect to both the locations and on- and offtimings of the cooling. Figure 2 shows the locations in the die where water cooling is used (labeled CC) and the on- and off-timings for each channel. Note: only the relative water-on durations are provided. The heat transfer phenomena occurring during water cooling in the die are complicated for both the water-on and -off stages. When water is flowing (i.e. water-on) to a cooling location, heat is removed by forced convection. When water begins to flow to a location, boiling will occur for a short period of time because the die temperature is relatively high (i.e. 300-500C). When cooling water flow is turned off, heat will continue to be extracted from the die as the water remaining in the channel boils. Eventually, the residual water will evaporate leaving the cooling channel dry, which reduces heat transfer from the die.
From the modeling perspective, the heat transfer for the water-on stage is described by a thermal boundary condition:
qcc = hcc(Tsurf – Twater) (1) where qcc is the heat flux, hcc is the heat transfer coefficient (HTC), and Tsurf and Twater are the surface temperature and water temperature, respectively. hcc is determined using the method developed in reference [3], which is provides a temperature-dependent relationship incorporating the effects of boiling.
At the water-off stage, a constant heat flux (derived by a trial-and-error method) is applied to represent the heat removed by the residual water (including boiling). It is acknowledged that this method is a simplified description that may be improved using a calculated temperature-dependent HTC.
However, this requires the application of two temperature-dependent HTCs on one boundary, corresponding to the two stages (time-periods), i.e. water-on and water-off. This requires the use of usersubroutines in ProCAST and was not available for this study. Heat transfer to the environment - heat loss through the die outer surface to the ambient environment in the pressure chamber occurs via two mechanisms: air convection and radiation. In the model, the convective HTC is set to 20 W/(m2K) and the environment temperature to 85C (measured). For radiation, an emissivity of 0.8 is used with the same environment temperature.
Inlet temperature - the temperature of the incoming metal is set to 700C at the entrance to the sprue based on the average temperature of liquid aluminum measured in the holding furnace.
3.4.2. Interface heat transfer. The heat transfer across the casting/die and die/die interfaces exhibits a variety behaviors including time, temperature and location dependence. For the die/die interfaces that maintain contact throughout the casting process, e.g. the top die/center pin interface, a constant interface HTC is applied. In contrast, some die/die interfaces are broken at specific times in a casting cycle to facilitate different operations. For example, when the die system opens, the top die/bottom die interface is broken and the exposed surfaces on both dies are open to the environment. In the model, the contact interface (boundary) condition is changed to an environment boundary condition (refer to the previous section) for the two surfaces.
Turning to the casting/die interface, this interface starts with a HTC selected to represent liquid metal in contact with the solid die during the filling stage. As the casting solidifies at the interface, the interface changes to a solid (casting)/solid (die) type of interface. For this type of contact, depending on the temperature field and geometrical structure of the die system, the solid/solid interface can experience increased pressure across the interface or the formation of a gap between the two surfaces due to thermal contraction/expansion. At the end of solidification, once the die is opened and the casting is ejected, the casting/die interface is broken and the environmental boundary condition is applied to all exposed surfaces. In the current version of the model, a temperature-dependent interface HTC has been adopted to describe the heat transfer associated with the aforementioned interface behavior. A typical interface HTC profile as a function of temperature is given in figure 3. The interface HTC is high when the liquid metal of the casting is in contact with the die and decreases linearly as solidification and thermal contraction occur. Enhanced interfacial HTC due to increased interface pressure has not been implemented in this model at this time.
3.4.3. Fluid flow boundary conditions. Pressure inlet - the fluid flow during filling in the CPC process is driven by the pressure difference, referred to as the counter pressure between the metal holding furnace and the pressure chamber. Currently, the model employs a pressure inlet boundary condition during the filling process. Note that the computational domain of the model does not include the transfer tube underneath the sprue, and therefore the pressure applied at the model inlet has been modified to offset the pressure needed to fill the transfer tube – equation 2.
Pmodel = Pcounter – ρA356ghtube (2)
where Pmodel is the pressure applied at the model inlet, Pcounter is the counter pressure, ρA356 is the density of aluminum alloy A356, g is the acceleration due to gravity and htube is the height of the transfer tube between the sprue and the liquid metal surface in the holding furnace.
It should be pointed out that from the modeling perspective, the only difference between the LPDC process and the CPC process is the pressure curve implemented. The LPDC process uses the furnace pressure as an input for the pressure inlet, while the CPC uses the counter pressure. In both processes, adequate venting is required during the filling stage to ensure that no back pressure develops.
3.5. Simulation settings
In ProCAST, the time-steps were dynamically updated to meet the solution convergence tolerance. The initial time-step size and maximum time-step size were defined for the filling and solidification stages, respectively. Tests were conducted to ensure that the default convergence tolerance was adequate for this model. Time-steps of 0.001s, 0.1s and 1s were used for the initial time-step size and the maximum time-steps for the filling and solidification stages, respectively.
Industrial production process assessment
An operational, industrial-scale CPC process was instrumented with 65 Type-K thermocouples (TCs) as follows: 31 in the top die, 13 in the bottom die, 3 in the casting component, 5 in the environment surrounding the die, 9 in the cooling channels and 4 in the bottom plate. Temperature data was collected from these thermocouples to provide a comprehensive and quantitative understanding of the temperatures in the process and to validate the model.
Results and discussion
5.1. Temperature
The temperatures were measured for 13 cycles over 1 hour. The near steady-state cyclic response from the process was identified and the temperature history from 6 TCs will be presented to define the characteristic behavior of the process. Figure 4 shows the measured temperatures for 3 TCs located in the top die (labeled TC3, TC9 and TC12), and 3 in the bottom die (labeled TC36, TC42 and TC46) – refer to figure 2 for their locations. The temperatures predicted by the model are also plotted in figure 4 for comparison. Firstly, looking at the measured data, in general, the temperature histories exhibit a similar pattern.
The temperatures are relatively low at the beginning of the cycle for a period of time before the liquid metal has filled the die – the system is building up pressure in the holding furnace and the pressure chamber. Once the liquid aluminum starts to fill into the die cavity, the die heats up, and consequently, the measured temperatures show a rapid rise as the heat diffuses to the TC locations (between ~40s to ~70s). The water-cooling is turned on with the sequence shown in figure 2(b). Within the die, once the rate of the heat removal, due to water-cooling and diffusion to cooler areas of the die, surpasses the heat supplied (from the casting), the temperature decreases – after ~75s. Another observation based on comparing the data from the top and bottom dies is that there are significant temperature gradients in the top die (e.g. TC12 and TC3 starts at ~290C and 430C, respectively). In contrast, the bottom die temperatures appear very close (within ~20C of each other). This observation was attributed to the fact that the top die has 7 active water-cooling locations and the bottom die has none. Turning to the comparison between the predicted and the measured temperatures, overall the model predictions correlate well with the measurements at all six locations. This indicates that the model has incorporated the key physics properly with respect to both heat transfer and fluid flow. However, it can be seen that at some locations, e.g. TC3 and TC9, the fit is relatively poor in the peak temperature region (~60s to ~120s). It is speculated that the simplified description of the complicated casting/die interface behavior may be reason for this discrepancy. Recent research has confirmed that the interface behavior during the casting process, particularly the casting/die interface, is very complicated due to the formation and evolution of an air gap or contact pressure along the interface caused by thermal contraction/expansion. A coupled temperature-fluid flow-displacement analysis is needed to properly describe this behavior because the deformation and heat transfer across the interface influence each other.
5.2. Solidification direction (shrinkage-based porosity)
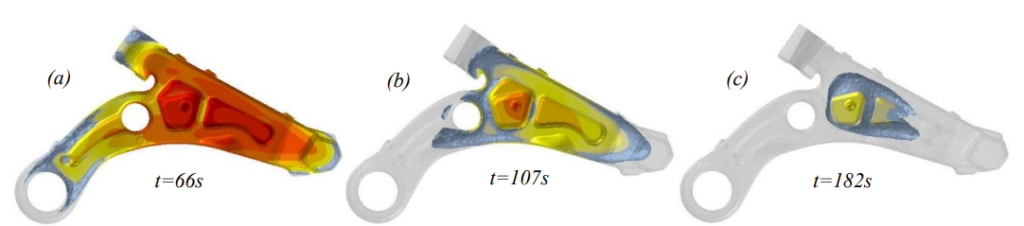
The solidification direction predicted by the model has been used to assess likely locations of shrinkageporosity formation. The desired direction is that the solidification occurs from the farthest end of the casting and works its way towards the inlet of liquid (sprue) – the so-called directional solidification. Failure to directional solidification leads to liquid encapsulation and may cause shrinkage-based porosity. However, a quantitative correlation between liquid encapsulation and shrinkage-based porosity has not been established, even though large and long-lasting liquid encapsulation is prone to form shrinkage-based porosity. Examination of the model results (figure 5) shows that, in general, directional solidification is achieved and only one small liquid encapsulation is observed existing for 4 s (figure 5(b)). Porosity in exemplar control arm castings was examined by Computed Tomography (CT) imaging (figure 6). CT results confirm that there are no locations of large-sized shrinkage porosity. Some smallsized porosity was found at the two locations highlighted in figure 6(b). The small number and size of this porosity and the fact that it occurs in non-critical locations permits these casting to pass inspection.
Summary
A numerical modelling methodology has been developed using ProCAST for the industrial CPC process of aluminum automotive parts. The model incorporates the key process boundary conditions and material properties. Validation against data measured on the production process has demonstrated the model’s accuracy. Given that the modelling methodology was originally developed for the LPDC process and has also been validated by the measured data from a LPDC process for wheel production, it proves the modelling methodology is robust and applicable for both the LPDC and CPC processes. Acknowledgement The authors thank CITIC Dicastal Co. Ltd for the technical and financial support of this work.
References
[1] Nishida Y, Droste W and Engler S 1986 Metall. Mater. Trans. B 17 833–44
[2] Wei X 2014 Thermal mechanical analysis of interfacial behavior in aluminum alloy wheel casting process (University of British Columbia)
[3] Moayedinia S 2014 Quantification of cooling channel heat transfer in low pressure die casting (University of British Columbia)
[4] Hu H, Chen F, Chen X, Chu Y L and Cheng P 2004 J. Mater. Process. Technol. 148 57–67
[5] Zhang B, Maijer D M and Cockcroft S L 2007 Mater. Sci. Eng. A 464 295–305
[6] Vijayaram T R 2012 Metalworld 24–6
[7] Mills K C 2002 Recommended values of thermophysical properties for selected commercial alloys (Woodhead Publishing)