A Review of the Taguchi Method for Minimizing Part Shrinkage in HDPE Injection Molding

This technical brief is based on the academic paper "Review on Optimization of Injection Molding Process Parameter for Reducing Shrinkage of High Density Polyethylene (HDPE) material" by Harshal P. Kale and Dr. Umesh V. Hambire, published in the International Journal of Science and Research (IJSR) (2015). It is summarized and analyzed for injection molding professionals by the experts at STI C&D.

Keywords

• Primary Keyword: Injection Molding Shrinkage Optimization
• Secondary Keywords: HDPE Shrinkage, Taguchi Method Injection Molding, Process Parameter Optimization, ANOVA Shrinkage Analysis, Injection Molding Defects, S/N Ratio Optimization

Executive Summary

• The Challenge: Shrinkage is a persistent quality issue in injection molding, leading to dimensional inaccuracies and rejected parts. Optimizing the numerous process parameters to minimize shrinkage is a complex, time-consuming, and often costly task.
• The Method: This paper reviews the application of the Taguchi method, a robust Design of Experiments (DOE) technique, to efficiently determine the optimal injection molding conditions for minimizing shrinkage in High-Density Polyethylene (HDPE).
• The Key Breakthrough: The Taguchi method, using Signal-to-Noise (S/N) ratios, allows engineers to identify the most influential process parameters and their optimal levels with a significantly reduced number of experimental trials compared to traditional methods.
• The Bottom Line: By applying the principles reviewed in this paper, manufacturers can develop a process that is less sensitive to uncontrollable variations, leading to higher-quality parts, reduced scrap rates, and significant cost savings.

The Challenge: Why This Research Matters for HPDC Professionals

Injection molding is a cornerstone of modern manufacturing, capable of producing intricate plastic parts with excellent dimensional accuracy. However, as the paper highlights, the process is not without its challenges. A primary concern is part shrinkage, which occurs as the polymer cools and solidifies in the mold cavity. This phenomenon can compromise the dimensional integrity of the final product, leading to assembly issues and part failure.

The difficulty lies in the sheer number of variables that influence shrinkage. As noted in the paper, the process is influenced by four major elements: the molder, the material, the injection machine, and the mold itself. Process parameters such as melt temperature, injection pressure, packing pressure, and cooling time all interact in complex ways. Manually tuning these parameters through trial and error is inefficient and expensive. This review addresses this critical industry problem by examining a systematic, data-driven approach to achieve process stability and minimize defects.

The Approach: Unpacking the Methodology

To tackle the complex problem of shrinkage, this paper reviews the use of the Taguchi method. This powerful statistical technique for process optimization is designed to make products and processes "robust," or insensitive to uncontrollable variations (referred to as "noise factors").

The core of the methodology, as described in the paper, involves:

• Orthogonal Array Experiments: Instead of testing every possible combination of parameters, the Taguchi method uses special experimental designs called orthogonal arrays. This allows for the study of the entire parameter space with a minimal number of experiments, saving significant time and resources.
• Signal-to-Noise (S/N) Ratio: The Taguchi method uses the S/N ratio to measure quality. For shrinkage, the goal is minimization, so the "Smaller-the-better" S/N ratio is used. A higher S/N ratio indicates a more robust process where the output (part dimension) is less affected by noise, resulting in more consistent quality.
• Systematic Optimization: The approach involves three stages: Concept Design, Parameter Design, and Tolerance Design. The review focuses on Parameter Design, where the optimal settings for control factors are determined without increasing manufacturing cost.

By using this structured approach, engineers can move beyond guesswork and systematically identify the process settings that yield the highest quality and consistency.

The Breakthrough: Key Findings & Data

This review synthesizes findings from multiple studies, confirming the effectiveness of the Taguchi method for shrinkage optimization. The key takeaways are:

• Efficient and Effective Optimization: The primary finding is that the Taguchi method is a "powerful and effective method" for solving complex quality problems in injection molding. It provides a much-reduced variance for experiments while identifying the optimum settings for process control parameters.
• Identification of Critical Parameters: The review cites research (e.g., Liao et al. [13], Chang and Faison [12]) indicating that packing pressure is often the most important parameter affecting shrinkage and warpage. Other significant factors consistently identified include melt temperature, mold temperature, holding pressure, and holding time.
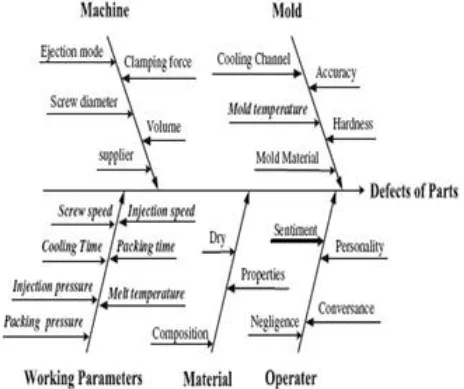
• A Framework for Analysis: The paper presents a clear cause-and-effect diagram (Figure 3) that visualizes the multiple sources of defects, including machine, mold, material, and operator factors. This serves as an excellent tool for root cause analysis in a production environment.
• Quantitative Shrinkage Measurement: A clear formula for calculating shrinkage is provided: S = (Dm-Dp) / Dm X 100, where Dm is the mold dimension and Dp is the final part dimension. This standardized measurement is essential for evaluating the success of optimization efforts.

Practical Implications for Your HPDC Operations

The findings reviewed in this paper offer direct, actionable insights for improving real-world manufacturing operations.

• For Process Engineers: The research strongly suggests that implementing a Taguchi DOE approach can dramatically accelerate process optimization. Instead of ad-hoc adjustments, engineers can use orthogonal arrays to systematically find the optimal settings for melt temperature, packing pressure, and cooling time, directly leading to reduced shrinkage and lower scrap rates.
• For Quality Control: The concept of using the S/N ratio provides a more advanced metric for process capability. Instead of just tracking the average shrinkage, monitoring the S/N ratio helps ensure the process is robust and less susceptible to daily variations in ambient conditions or material batches, as highlighted in the paper's conclusion.
• For Die Design: The cause-and-effect diagram (Figure 3) explicitly connects mold design features like "Cooling Channel" and "Mold Temperature" to part quality. This reinforces the principle that process optimization cannot be done in a vacuum; it must be considered in conjunction with robust mold design to achieve the best results.

Paper Details

Review on Optimization of Injection Molding Process Parameter for Reducing Shrinkage of High Density Polyethylene (HDPE) material

1. Overview:

• Title: Review on Optimization of Injection Molding Process Parameter for Reducing Shrinkage of High Density Polyethylene (HDPE) material
• Author: Harshal P. Kale, Dr. Umesh V. Hambire
• Year of publication: 2015
• Journal/academic society of publication: International Journal of Science and Research (IJSR)
• Keywords: Injection molding, Taguchi method, shrinkage, H.D.P.E.

2. Abstract:

Injection molding is the most widely used polymeric fabrication process. It evolved from metal die casting; however, unlike molten metal, polymer melts have a high viscosity and cannot simply be poured into a mold. Instead, a large force must be used to inject the polymer into the hollow mold cavity. More melt must also be packed into the mold during solidification to avoid shrinkage in the mold. In this paper, a review on optimal injection molding conditions for minimum shrinkage was determined by the DOE technique of Taguchi methods. The various observations have been taken for material namely HDPE. The determination of optimal process parameters was based on S/N ratios.

3. Introduction:

Injection molding is the most common method for producing plastic parts. The process involves injecting heated molten plastic into a mold, where it cools and solidifies. It is capable of producing an infinite variety of complex parts. The process is influenced by four major elements: the molder, the material, the injection machine, and the mold. This review focuses on optimizing the process parameters to control defects like shrinkage, which is a critical quality characteristic.

4. Summary of the study:

Background of the research topic:

The research addresses the challenge of shrinkage in injection-molded parts made from High-Density Polyethylene (HDPE). Shrinkage is a natural consequence of the polymer cooling and solidifying, but excessive or non-uniform shrinkage leads to dimensional inaccuracies and defects. Optimizing the process is crucial for producing high-quality parts consistently.

Status of previous research:

The paper reviews several studies that have successfully used the Taguchi method and ANOVA to optimize injection molding parameters. Researchers like Oktem et al. [9], Shen et al. [11], and Liao et al. [13] have applied these techniques to reduce warpage and shrinkage by determining optimal settings for parameters like packing pressure, packing time, injection time, and cooling time. The review confirms that packing pressure and time are frequently identified as the most significant parameters.

Purpose of the study:

The purpose of this paper is to review the application of the Taguchi method as a Design of Experiments (DOE) technique for determining the optimal injection molding conditions to achieve minimum shrinkage. The study focuses specifically on HDPE material and the use of Signal-to-Noise (S/N) ratios for optimization.

Core study:

The core of the study is the review and synthesis of the Taguchi philosophy for process optimization. It explains how this method uses orthogonal arrays to reduce the number of required experiments, making it a time- and cost-effective alternative to classical experimental design. The paper emphasizes the use of the S/N ratio as a performance measure to develop products and processes that are insensitive to "noise" factors (uncontrollable variables), thereby improving quality and consistency. The "Smaller-the-better" S/N ratio is identified as the appropriate metric for minimizing shrinkage.

5. Research Methodology

Research Design:

The paper is a literature review. It analyzes and summarizes previous research that has applied the Taguchi method and ANOVA for the optimization of injection molding process parameters. The design is based on three stages of Taguchi's optimization strategy: Concept Design, Parameter Design, and Tolerance Design, with a focus on Parameter Design.

Data Collection and Analysis Methods:

The methodology reviewed is the Taguchi method. This involves:

1. Identifying control factors (e.g., melt temperature, injection pressure, packing pressure, etc.).
2. Designing an experiment using an orthogonal array.
3. Conducting the experimental runs.
4. Calculating the S/N ratio for the results. For shrinkage, the "Smaller-the-better" formula is used: S/N = -10 log 10(1/n Σ yi²).
5. Analyzing the S/N ratios to determine the optimal level for each control factor.

Research Topics and Scope:

The scope of the review is the optimization of injection molding process parameters to reduce shrinkage in HDPE material. It specifically investigates the application and effectiveness of the Taguchi and ANOVA methods for this purpose.

6. Key Results:

Key Results:

The review concludes that the Taguchi method is a robust and efficient technique for optimizing injection molding processes. It successfully identifies the optimal settings of process variables to make the product/process insensitive to uncontrollable environmental factors. The review of literature confirms that parameters such as melt temperature, injection pressure, packing pressure, packing time, and cooling time are critical factors affecting the shrinkage of HDPE material. The use of S/N ratios provides a reliable metric for achieving a process that is stable and produces minimal shrinkage.

Figure Name List:

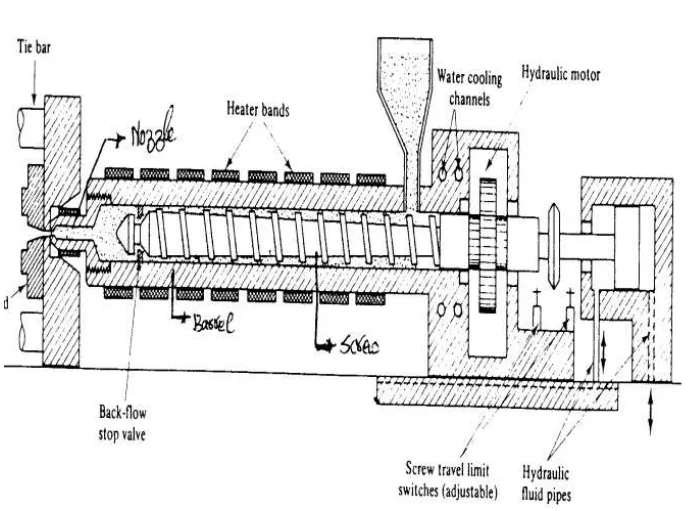
• Figure 1: Injection molding machine set up
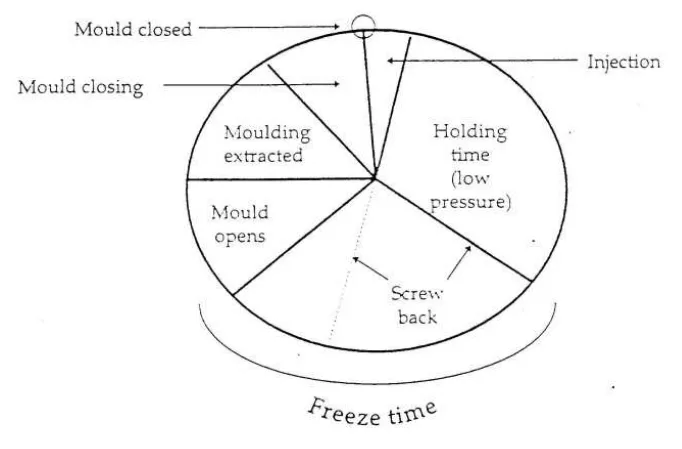
• Figure 2: Cycle of Operations
• Figure 3: Cause and Effect Diagram

7. Conclusion:

A review of literature on optimization techniques revealed that Taguchi methods are successful, robust design techniques widely used in industries. They help make a product or process insensitive to uncontrollable factors, saving experimental time and cost. The paper concludes that Taguchi and ANOVA methods were effectively used in the reviewed literature to investigate the effects of melt temperature, injection pressure, packing pressure, packing time, and cooling time on the shrinkage of HDPE material, providing a clear path to quality improvement.

8. References:

• [1] Chang TC, Faisen E."Shrinkage behavior and optimization of injection molded parts studied by the Taguchi method", polymer Engg Sci 2001; 41:703-10.
• [2] H. Zhou, Y. Zhang J. Wen, D. Li "an acceleration method for minimization of shrinkage" International Journal of Advance Manufacturing Technology, 37, pp1006-1022.
• [3] Mohd. Muktar Alam, Deepak Kumar, "Reducing shrinkage in plastic injection moulding using Taguchi method in Tata magic head light", International journal of science and research (IJSR), India onlineISSN:2319-70654.
• [4] K. Krishnaiah, P. Shahabudeen,”Applied design of experiment and Taguchi method", PHI learning private limited. Delhi-110092. 2013.
• [5] Vaatainen O, pentti J "Effect of processing parameters on quality of injection molded parts using Taguchi parameter design method", plastic Rubber Compos1994:21:2117.
• [6] Sajjan Kumar Lal, Dr. Hari Vasudevan, " Optimization of injection molding process parameter in the molding of Low Density polyethylene (LDPE)", International journal of Engineering Research and Development, e-ISSN:2278-067X, p-ISSN:2278-800X, volume 7, issue 5, pp. 35-39.
• [7] S. Kamaruddin, Zahid A. Khan and S. H. Foong, "Application of Taguchi method in the Optimization of Injection moulding parameters for manufacturing products from plastic blend", IACSIT international journal of engineering and technology, vol2, no 6, December2010.
• [8] Shi W. Lee, Seokyoung Ahn, "Effect of process parameter in plastic, metal and ceramic injection molding process", Korea-Australia Rheology journal, vol 123, No3, september2011, pp127-138.
• [9] D. Mathivanan, M. Nouby and R. Vidhya, "Minimization of sink markdeffectsin injection molding process Taguchi approach", International journal of Engineering Science and Technology, vol 2, No 2, 2010, pp 13-22.
• [10] M. Stanek, D. Manas, M. Manas, O Suba, "Optimization of injection molding process", International journal of Mathematics and computers in simulation, issue 5, volume 5, 2011, pp 413-421.
• [11] Aliraza Akbarzadeh and mohammad Sadhegi, "parameter study in plastic Injection molding process using statistical method and IWO algorithm", International Journal of molding and optimization, volume1, No 2, June 2011, pp 141-145.
• [12] M. V. Kavade, S. D. Kadam, "Parameter optimization of injection molding of polypropylene by using Taguchi methodology:, IOSR Journal of Mechanical and Civil Engineering(IOSR-JMCE), ISSN:22781684, volume 4, issue 4, pp 49-58.
• [13] G. Pötsch and W. Michaeli, "Injection moulding: An introduction", Munich: Hanser Publishers, 1995.
• [14] J. A. Brydson, "Plastic materials", Butterworth-Heinmann: Oxford, 1995.
• [15] D. V. Rosato, M. G. Rosato, "Injection moulding handbook" Massachusetts: Kluwer Academic Publishers, 2000.
• [16] M. C. Huang and C. C. Tai, "The effective factors in the warpage problem of an injection-moulded part with a thin shell feature", J. Mat. Proc. Tech., vol. 110, 2001, pp. 1-9.
• [17] M. Altan, “Reducing Shrinkage in Injection Mouldings via the Taguchi, ANOVA and Neural Network Methods", j. Mat. & Design, vol. 31, 2010, pp. 599–604
• [18] Neeraj Singh Chauhan and Shahzad Ahmad "Optimization of Cycle Time of DVD-R Injection Moulding Machine" by International Journal of Engineering and Technology (IJES

Conclusion & Next Steps

This research provides a valuable roadmap for enhancing quality in HDPE injection molding. The findings offer a clear, data-driven path toward reducing defects like shrinkage, improving process consistency, and optimizing production efficiency.

STI C&D is committed to applying cutting-edge industry research to solve our customers’ most challenging technical problems. If the problem discussed in this white paper aligns with your research goals, please contact our engineering team to discuss how we can help you apply these advanced principles to your research.

Expert Q&A:

• Q1: What is the primary goal of using the Taguchi method for injection molding as described in this review?
  • A1: The primary goal is to determine the optimal set of process parameters (like melt temperature, injection pressure, packing pressure) to minimize shrinkage in the final part. The method aims to create a robust manufacturing process that is insensitive to uncontrollable "noise" variables, thereby improving quality and consistency. This is supported by the paper's abstract and conclusion.
• Q2: According to the reviewed literature, which process parameters are most significant in affecting shrinkage?
  • A2: The review cites multiple studies (e.g., [12], [13]) that identify packing pressure as a highly significant factor. Other critical parameters mentioned are mold and melt temperatures, holding pressure, and holding time.
• Q3: How does the Taguchi method reduce the time and cost of experiments?
  • A3: The Taguchi method uses special designs called orthogonal arrays to study the entire factor space with only a small number of experiments. This is a significant advantage over classical experimental designs which are time-consuming and require many experiments when the number of control factors is high, as stated in Section 4 of the paper.
• Q4: What is the "Smaller-the-better" S/N ratio, and why is it used for shrinkage?
  • A4: The "Smaller-the-better" S/N ratio is a statistical measure used in the Taguchi method when the goal is to minimize a certain characteristic. Its formula is S/N = -10 log 10(1/n Σ yi²). It is used for shrinkage because the objective is to make the shrinkage value as small as possible, as explained in Section 4.1.
• Q5: How is shrinkage quantitatively measured in this context?
  • A5: Shrinkage (S) is calculated as the difference between the mold cavity dimension (Dm) and the finished part dimension (Dp), divided by the mold dimension, and expressed as a percentage. The formula is S = (Dm-Dp) / Dm X 100, as detailed in Section 4.2 of the paper.
• Q6: Besides process parameters, what other factors can cause defects in injection molding?
  • A6: The Cause and Effect Diagram in Figure 3 shows that defects can arise from four main areas: the Machine (e.g., screw diameter), the Mold (e.g., cooling channel design, mold material), the Material (e.g., properties, composition), and the Operator (e.g., negligence, experience).

Copyright

• This material is an analysis of the paper "Review on Optimization of Injection Molding Process Parameter for Reducing Shrinkage of High Density Polyethylene (HDPE) material" by Harshal P. Kale and Dr. Umesh V. Hambire.
• Source of the paper: International Journal of Science and Research (IJSR), ISSN (Online): 2319-7064, Volume 4 Issue 4, April 2015.
• This material is for informational purposes only. Unauthorized commercial use is prohibited.
• Copyright © 2025 STI C&D. All rights reserved.