Sebastian Kohlstädt* and Michael Vynnycky
Department of Materials Science and Engineering,
KTH Royal Institute of Technology,
Brinellvägen 23,
100 44 Stockholm, Sweden
Email: skoh@kth.se
Email: michaelv@kth.se
*Corresponding author
Abstract
In this work, the implementation of three turbulence models inside the open source C++ computational fluid dynamics (CFD) library OpenFOAM were tested in 2D and 3D to determine the viability of salt cores in high pressure die casting. A finite-volume and volume of fluid approach was used to model the two-phase flow of molten metal and air, with the latter being treated as compressible. Encouragingly, it is found that, although the choice of turbulence model seems to affect the dispersion of the two-phase interface, the force acting at the surface of the salt core depends only very weakly on the turbulence model used. The results were also compared against those obtained using the commercially available and widely-used casting software MAGMA5.
Keywords
RANS; volume-of-fluid method; OpenFOAM; high pressure die casting;
HPDC; aluminium; lost cores; salt core viability.
Introduction
High pressure die casting (HPDC) is an important process for manufacturing high volume and low cost automotive components, such as automatic transmission housings and gear box components. Liquid metal, generally aluminium, is injected through complex gate and runner systems and into the die at high speed, typically between 50 and 100 ms−1, and under very high pressures.
However, it has up to date proven difficult to employ lost cores within the process. The basic idea of using salt cores is to create undercuts or hollow sections with them, which may then later act as cooling or oilflow channels. Given this process constraint in design freedom for the CAD-engineer, the idea of using salt as the material for lost cores has been put forward by machine manufacturers, as well as automotive companies (Jelínek and Adámková, 2014).
One way to determine whether this is indeed viable is to employ numerical simulation. However, such studies are certainly far from exhaustive. The only examples of core viability simulation that we have been able to find are those due to Fuchs et al. (2013) and Fuchs and Körner (2014), who employed the commercial computational fluid dynamics (CFD) software Flow-3D, in order to compute the nonisothermal, turbulent, multiphase (molten metal/air) flow that occurs. In both cases, RANS (Reynolds Averaged Navier Stokes) modelling was adopted to take account of the turbulence, via the use of the Renormalised Group (RNG) k-ε model (Yakhot et al., 1992).
The RNG model is considered to be a more robust version of the two-equation k-ε model (Launder and Spalding, 1974), and is recommended for most industrial problems. It extends the capabilities of the standard k-ε model to provide better coverage of transitionally turbulent flows, curving flows, wall heat transfer, and mass transfer. In this context, the purpose of this paper is twofold.
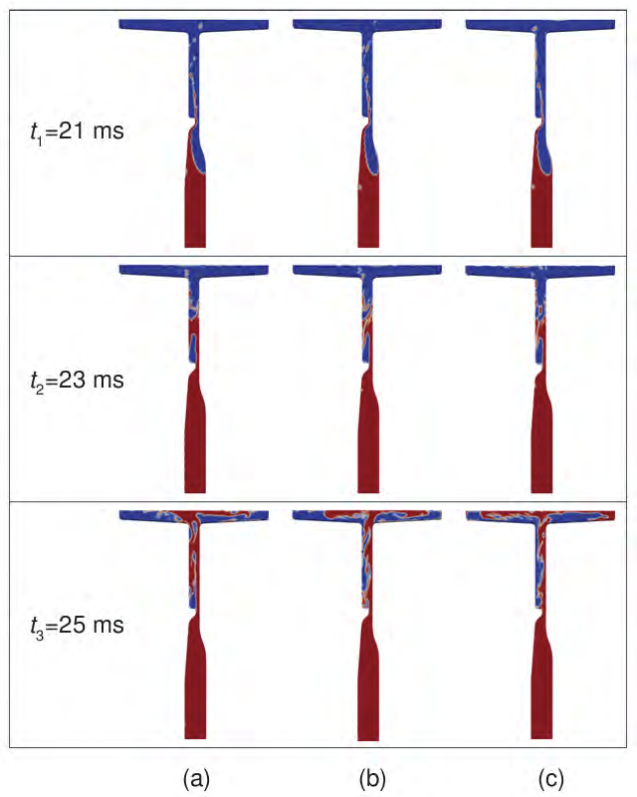
The first will be to examine whether the choice of RANS turbulence model affects the stress on the salt core, and hence its viability. The second is to commence to move away from the use of commercial software and towards the development of open source software for HPDC modelling.
To achieve these goals, we use the open-source C++ CFD library OpenFOAM (Weller et al., 1998; Jasak et al., 2007) and employ the k-ε, k-ω-SST (shear stress transport) (Menter, 1994) and Spalart-Allmaras turbulence models (Spalart and Allmaras, 1994), together with the volume of fluid (VOF) method (Hirt and Nichols, 1981) to take account of the multiphase flow.
We have chosen these three models because they are the ones most often used for turbulent engineering computations. The simplest of these is the Spalart-Allmaras model, which is a so-called one-equation model which solves a transport equation for a viscosity-like variable that is often referred to as the Spalart-Allmaras variable.
On the other hand, the k-ε model is a two-equation eddy-viscosity model which solves transport equations for the turbulent kinetic energy, k and the dissipation ε. As for the k-ω SST model, it is also a two-equation model, although it solves transport equations for k and the specific dissipation rate, ω; however, unlike its predecessor, the k-ω model, it solves for k and ω in nearwall regions, but for k and ε in the free stream away from wall regions.
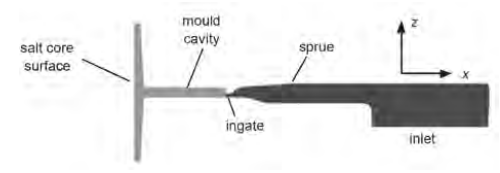
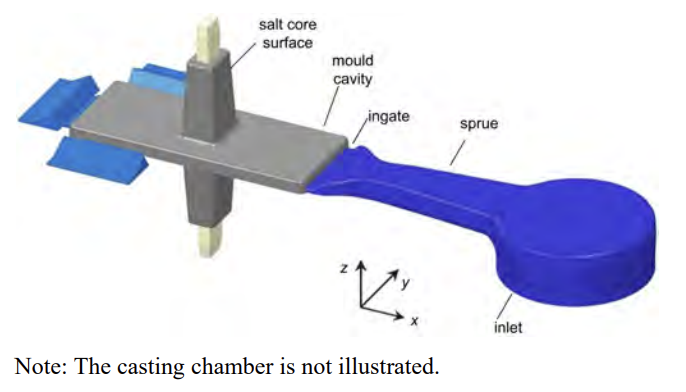
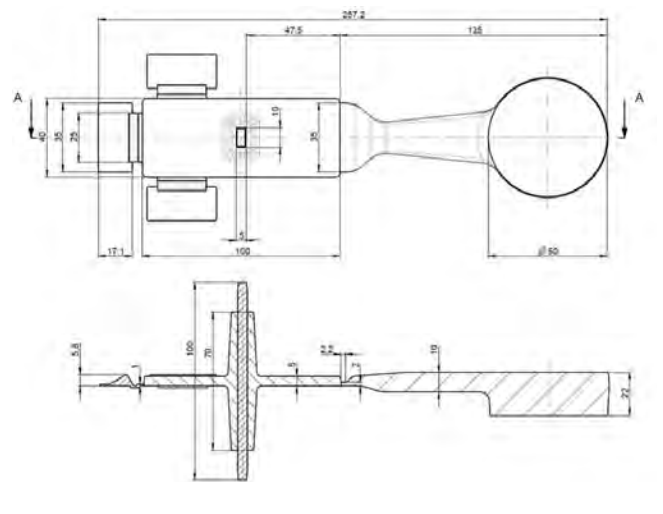
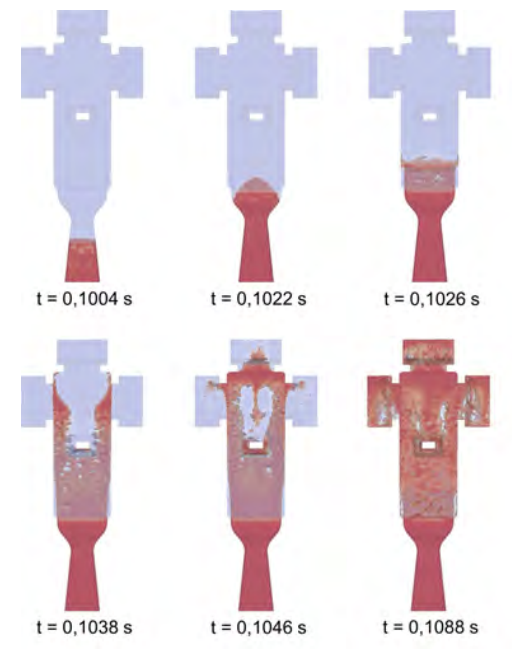
The performance of the three models is compared for a two-dimensional flow containing a core, as given in Figure 1, and then the k-ω-SST model is used for 3D computations for the flow in the geometry shown in Figures 2 and 3; for the latter case, the results are compared with those obtained using the commercial casting software MAGMA5.
References
Beitz, W., Küttner, K.H. and Davies, B.J. (2013) DUBBEL –Handbook of Mechanical Engineering, Springer-Verlag London.
Brackbill, J.U., Kothe, D.B. and Zemach, C. (1992) ‘A continuum method for modeling surface tension’, Journal of Computational Physics, Vol. 100, No. 2, pp.335–354.
Cleary, P.W., Ha, J., Prakash, M. and Nguyen, T. (2006) ‘3D SPH flow predictions and validation for high pressure die casting of automotive components’, Applied Mathematical
Modelling, Vol. 30, No. 11, pp.1406–1427.
Courant, R., Friedrichs, K. and Lewy, H. (1967) ‘On the partial difference equations of mathematical physics’, IBM Journal of Research and Development, Vol. 11, No. 2, pp.215–234.
Ferrer, P.J.M., Causon, D.M., Qian, L., Mingham, C.G. and Ma, Z.H. (2016) ‘A multi-region coupling scheme for compressible and incompressible flow solvers for two-phase flow in a numerical wave tank’, Computers and Fluids, Vol. 125, pp.116–129.
Fuchs, B., Eibisch, H. and Körner, C. (2013) ‘Core viability simulation for salt core technology in high pressure die casting’, International Journal of Metalcasting, Vol. 7, No. 3,
pp.39–45.
Fuchs, B. and Körner, C. (2014) ‘Mesh resolution consideration for the viability prediction of lost salt cores in the high pressure die casting process’, Progress in Computational Fluid Dynamics, Vol. 14, No. 1, pp.24–30.
Ha, J., Cleary, P.W., Alguine, V. and Nguyen, T. (1999)
‘Simulation of die filling in gravity die casting using SPH and MAGMASoft’, Proceedings of the 2nd International Conference on CFD in Minerals and Process Industries,
Melbourne, Australia, pp.423–428.
Ha, J., Cleary, P.W., Prakash, M., Alguine, V., Nguyen, T. and Scott, C. (2003) ‘SPH, MAGMASoft and water analogue modellings of die filling of a servo piston’, Proceedings of the 2nd International Conference on CFD in Minerals and Process Industries, Melbourne, Australia, pp.587–592.
Hirt, C.W. and Nichols, B.D. (1981) ‘Volume of fluid (VOF) method for the dynamics of free boundaries’, Journal of Computational Physics, Vol. 39, No. 1, pp.201–225.
Jasak, H., Jemcov, A. and Tuković, ˇZ. (2007) ‘OpenFOAM: a C++ Library for Complex Physics Simulations’, Paper presented at the International Workshop on Coupled Methods
in Numerical Dynamics IUC, Dubrovnik, Croatia, 19–21
September, 20pp. Jelínek, P. and Adámková, E. (2014) ‘Lost cores for high-pressure
die casting’, Archives of Foundry Engineering, Vol. 14,
No. 2, pp.101–104.
Koch, M., Lechner, C., Reuter, F., Köhler, K., Mettin, R. and Lauterborn, W. (2016) ‘Numerical modeling of laser generated cavitation bubbles with the finite volume and volume of fluid method, using OpenFOAM’, Computers and Fluids, Vol. 126, pp.71–90.
Launder, B.E. and Spalding, D.B. (1974) ‘The numerical computation of turbulent flows’, Computer Methods in Applied Mechanics and Engineering, Vol. 3, pp.269–289.
Mayon, R., Sabeur, Z., Tan, M-Y. and Djidjeli, K. (2016) ‘Free surface flow and wave impact at complex solid structures’, Paper presented at the 12th International Conference on Hydrodynamics, Egmond aan Zee, NL, 18–23 September, Paper ID: 154, 10pp.
Menter, F.R. (1994) ‘2-equation eddy-viscosity turbulence models for engineering applications’, AIAA Journal, Vol. 32, No. 8, pp.1598–1605.
Menter, F.R., Kuntz, M. and Langtry, R. (2003) ‘Ten years of industrial experience with the SST turbulence model’, Turbulence, Heat and Mass Transfer, Vol. 4, pp.625–632.
Nogowizin, B. (2010) Theorie und Praxis des Druckgusses,
Fachverlag Schiele & Schön.
Robertson, E., Choudhury, V., Bhushan, S. and Walters, D.K. (2015) ‘Validation of OpenFOAM numerical methods and turbulence models for incompressible bluff body flows’,
Comp. Fluids, Vol. 123, pp.122–145.
Spalart, P.R. and Allmaras, S.R. (1994) ‘A one-equation turbulence model for aerodynamic flows’, Recherche Aerospatiale, No. 1, pp.5–21.
Versteeg, H. and Malalasekera, W. (2007) An Introduction to Computational Fluid Dynamics: The Finite Volume Method, 2nd ed., Pearson.
Weller, H.G., Tabor, G., Jasak, H. and Fureby, C. (1998) ‘A tensorial approach to computational continuum mechanics using object-oriented techniques’, Computers in Physics, Vol. 12, No. 12, pp.620–631.
White, F.M. (2011) Fluid Mechanics, 7th ed., McGraw-Hill, New York.
Wilcox, D.C. (1988) ‘Reassessment of the scale determining equation for advanced turbulence models’, AIAA Journal, Vol. 26, No. 11, pp.1299–1310.
Yakhot, V., Orszag, S.A., Thangam, S., Gatski, T.B. and Speziale, C.G. (1992) ‘Development of turbulence models for shear flows by a double expansion technique’, Physics of Fluids A: Fluid Dynamics, Vol. 4, pp.1510–1520.
Yamada, Y. (2013) EP Patent No. 20090742774 (July 10, 2013)
Yaokawa, J., Miura, D., Anzai, K., Yamada, Y. and Yoshii, H. (2006) ‘Mechanical properties of salt core comprised of alkali carbonate and alkali chloride’, Journal of Japan Foundry
Engineering Society, Vol. 78, pp.1510–1520.