A Probabilistic Approach in Failure Modellingof AluminiumHighPressure Die-Castings

This technical summary is based on the academic paper "A Probabilistic Approach in Failure Modelling of Aluminium High Pressure Die-Castings" by Octavian Knoll, submitted as a Thesis for the degree of Philosophiae Doctor at the Norwegian University of Science and Technology and Karlsruhe Institute of Technology (2015). It has been analyzed and summarized for technical experts by CASTMAN with the assistance of AI.

Keywords

• Primary Keyword: Probabilistic Failure Modeling for HPDC
• Secondary Keywords: aluminum high pressure die-casting, casting defects, material ductility variation, Weibull distribution in casting, Cockcroft-Latham criterion, numerical simulation of die-castings, HPDC crashworthiness

Executive Summary

A 30-second overview for busy professionals.

• The Challenge: The inherent variability of casting defects in aluminum HPDC makes traditional deterministic failure models unreliable for predicting structural integrity, especially in crash-critical components.
• The Method: The research combined extensive mechanical testing of a generic AlSi9Mn HPDC component with the development of a novel probabilistic failure model based on the Cockcroft-Latham criterion and Weibull distribution.
• The Key Breakthrough: The study successfully demonstrated that a probabilistic approach can accurately predict failure probability from a single FE simulation, capturing the local pseudo-random material ductility variations that cause scatter in performance.
• The Bottom Line: Adopting probabilistic failure modeling allows for more reliable numerical design of HPDC parts, improving crashworthiness predictions and reducing the risks associated with material inconsistencies.

The Challenge: Why This Research Matters for HPDC Professionals

In modern automotive design, aluminum high-pressure die-castings (HPDC) are essential for creating lightweight, complex, and structurally critical components like nodes and connectors. These parts are expected to maintain structural integrity under extreme loads, such as in a crash scenario. However, the HPDC process itself introduces a significant challenge: casting defects.

Defects like shrinkage pores, gas porosity, and oxide films are an unavoidable consequence of the casting process. Crucially, these defects are not uniformly distributed. Their presence varies both systematically across a component (e.g., based on proximity to gating channels) and randomly due to minor fluctuations in the process. This leads to a strong and unpredictable variation in material ductility.

For engineers relying on Finite Element (FE) analysis for crash design, this presents a major problem. Traditional, deterministic failure models assume uniform material properties, which fails to account for this inherent scatter. This can lead to unreliable predictions of component failure, jeopardizing structural safety and performance. This research directly addresses the need for a more robust numerical design approach that embraces, rather than ignores, the material variability of HPDC components.

The Approach: Unpacking the Methodology

To tackle this challenge, the research employed a comprehensive experimental and numerical methodology.

Experimental Work:
The study centered on a generic, U-shaped HPDC component made of an AlSi9Mn alloy (Castasil-37) in its as-cast condition. An extensive material characterization program was performed using uniaxial tensile tests on specimens machined from various locations across multiple identical components. This meticulous sampling strategy allowed for the distinct measurement of both:
1. Global Systematic Variation: Differences in ductility based on the specimen's location relative to the casting system (e.g., gating side vs. vacuum side).
2. Local Pseudo-Random Variation: The scatter in ductility observed among specimens taken from the exact same position on different components.

Additionally, three-point bending and axial compression tests were performed on the full U-shaped component to analyze its structural behavior and validate the numerical models.

Numerical Work:
A novel Probabilistic Failure Modeling for HPDC approach was developed. The model integrated:
- An isotropic hypoelastic-plastic constitutive model to describe material deformation.
- The phenomenological Cockcroft-Latham failure criterion to define the onset of fracture.
- The weakest-link model by Weibull to describe the statistical distribution of the critical failure value, thereby capturing the local pseudo-random variation in ductility.

This model was implemented in four distinct user-defined material routines (MR#1 to MR#4) in the explicit FE solver LS-DYNA, allowing for direct comparison of different probabilistic simulation strategies.

The Breakthrough: Key Findings & Data

The research yielded several breakthroughs in applying probabilistic methods to HPDC component design, validating a more efficient and accurate approach to predicting failure.

Finding 1: Single-Simulation Failure Prediction Correlates with Monte-Carlo Analysis

A key challenge in stochastic simulation is the high computational cost of running hundreds of simulations for a Monte-Carlo analysis. This research demonstrated a more efficient path. Material routine MR#1 was developed to compute the failure probability directly from a single simulation. This was compared against a full Monte-Carlo analysis using 36 parallel simulations with material routine MR#2.

As shown in Figure 10.1.4, the results were remarkably consistent. The failure probability curve predicted by the single simulation (MR#1, solid blue line) showed excellent correlation with the failure probability estimated from the 36-run Monte-Carlo simulation (MR#2, blue triangles). This finding is significant because it proves that a reliable probabilistic assessment can be achieved with the computational effort of just one simulation, making the approach practical for industrial use.

Finding 2: Probabilistic Model Accurately Predicts Component-Level Failure

The ultimate test of a numerical model is its ability to predict the behavior of a real-world component. The study validated the probabilistic model by simulating the three-point bending test of the U900-1 component and comparing the numerical failure probability with the experimental failure probability derived from seven parallel tests.

The results, shown in Figure 10.3.6c, demonstrate a very good correlation between the experimental failure probability (red triangles) and the numerical failure probability obtained from the solid mesh model (blue line) and the hybrid mesh model (magenta line). This confirms that the probabilistic approach, when combined with correct material parameters and a sufficiently stiff structural model, provides a very good prediction of the failure probability of a complex HPDC component.

Practical Implications for R&D and Operations

Based on the paper's Discussion and Conclusion sections, provide conditional insights for different professional roles.

• For Process Engineers: This study suggests that adjusting the casting system design (e.g., gating and vacuum channel placement) may contribute to creating more homogenous material properties and reducing the global systematic variation in ductility.
• For Quality Control Teams: The data in Table 8.2.1 and the associated box-plot of the paper illustrates the effect of a specimen's extraction location on the critical failure value (Wc), which could inform new quality inspection criteria focused on the most vulnerable areas of a component (e.g., the vacuum side).
• For Design Engineers: The findings indicate that the choice of FE mesh (solid, shell, or hybrid) can significantly influence the stiffness representation and failure prediction. The hybrid mesh (Figure 10.3.1d) is presented as a computationally efficient alternative to a full solid mesh for capturing the stiffness of complex features like ejector domes, a valuable consideration in the early design phase for crash simulations.

Paper Details

A Probabilistic Approach in Failure Modelling of Aluminium High Pressure Die-Castings

1. Overview:

• Title: A Probabilistic Approach in Failure Modelling of Aluminium High Pressure Die-Castings
• Author: Octavian Knoll
• Year of publication: 2015
• Journal/academic society of publication: Thesis for the degree of Philosophiae Doctor, Norwegian University of Science and Technology (NTNU) and Karlsruhe Institute of Technology (KIT)
• Keywords: Probabilistic Failure Modeling for HPDC, aluminum high pressure die-casting, casting defects, material ductility variation, Weibull distribution in casting, Cockcroft-Latham criterion, numerical simulation of die-castings, HPDC crashworthiness

2. Abstract:

Aluminium high pressure die-castings have become essential elements of a modern car body in recent years. The high pressure die-casting method enables to produce thin walled components of complex geometries. This advantage is used to create structural nodes and connector elements as one-piece components. These components are subjected to extreme loads such as in crash situations and expected to maintain the structural integrity of the car body. Numerical models are required to analyse the structural behaviour of aluminium high pressure die-casting components and to guarantee their structural reliability. The material ductility in aluminium high pressure die-casting components is strongly influenced by casting defects. Typical casting defects are shrinkage pores, gas pores and oxide films. These casting defects are caused by the casting system and fluctuations during the casting process. As a result, the casting defects are varying within a component. Moreover, the variation can be separated into a global systematic variation depending on the casting system and a local pseudo-random variation caused by the process fluctuations. A casting defect can be considered as initial material damage which leads to a decrease of the local material ductility. As a result, the material ductility exhibits a global systematic variation and a local pseudo-random variation. The main objective of the present work is the experimental and numerical analysis of these two types of variation.

3. Introduction:

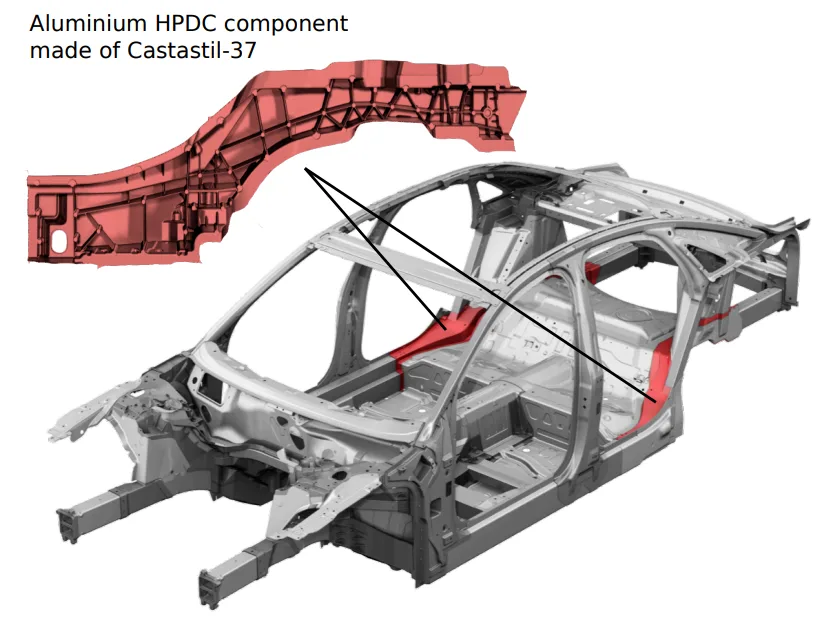
The lightweight design of a modern car body requires materials that offer weight reduction while increasing structural stiffness and crashworthiness. Aluminium HPDC components are essential for this, used as structural nodes and connectors where high forces are introduced. However, the material ductility of these components is dominated by casting defects, which causes significant variation within a single component. For reliable numerical design using the finite element method, particularly for crash simulations, this variation in material ductility must be taken into account. This research is motivated by large structural HPDC components in the Audi A8 car body, which are used in their as-cast condition, making the understanding of their failure behavior critical.

4. Summary of the study:

Background of the research topic:

The HPDC process, while enabling complex geometries, inherently produces casting defects such as porosity and oxide films. These defects act as initial material damage, significantly reducing and creating scatter in the material's ductility. This variation can be categorized into a global, systematic variation dependent on the casting system layout (e.g., gating vs. vacuum side) and a local, pseudo-random variation due to process fluctuations.

Status of previous research:

Previous research, as reviewed in Chapter 6, has established the use of standard metal plasticity models for the constitutive behavior of HPDC alloys. Ductile failure criteria, often in the form of fracture loci, are commonly used. Some studies have acknowledged the scatter in ductility and the influence of porosity, but few have integrated a rigorous probabilistic framework that separates global and local variations and validates the model on a component level in a stochastic sense.

Purpose of the study:

The main objective of the work is the development of a numerical material model that accurately predicts the deformation and failure behavior of aluminum casting alloys by considering the influence of casting defects on material ductility. The study aims to:
1. Experimentally analyze the variation in material ductility through component and material testing.
2. Develop and numerically implement a material model for aluminum HPDC.
3. Numerically analyze and validate the material model through FE simulations of the tests.

Core study:

The core of the study involved a comprehensive experimental program on a generic U-shaped HPDC component (U900-1) made of AlSi9Mn alloy. Tensile specimens were extracted from 15 different positions across 5 components to quantify both global and local ductility variations. Component-level bending and compression tests were also performed. This experimental data was used to calibrate and validate a probabilistic failure model based on the Cockcroft-Latham criterion and a weakest-link Weibull distribution, which was implemented in an explicit FE solver.

5. Research Methodology

Research Design:

The research was designed as a combined experimental and numerical investigation. The experimental part focused on quantifying material property variation, while the numerical part focused on developing and validating a model to predict this variation's effect on structural performance. A key aspect was the sampling strategy, using specimens from duplicated extraction positions to separate local pseudo-random scatter from global systematic variation.

Data Collection and Analysis Methods:

Data was collected from uniaxial tensile tests (force-elongation), component bending tests, and axial compression tests. The material ductility was quantified using the critical value of the Cockcroft-Latham integral (Wc). An extensive statistical analysis, including descriptive statistics, hypothesis testing (F-test, t-test, KS-test), and Anderson-Darling tests, was performed on the results to identify positions with comparable ductility and to characterize the statistical distribution of the failure properties.

Research Topics and Scope:

The scope was to develop a probabilistic failure modeling approach for as-cast aluminum HPDC alloys under quasi-static loading. The research covered:
- Experimental characterization of material ductility variation.
- Statistical analysis to describe this variation.
- Development of a probabilistic failure model combining a constitutive model and a randomized failure criterion.
- Numerical implementation into four user-defined material routines (MR#1-MR#4) in LS-DYNA.
- Validation of the model against component tests by comparing predicted failure probabilities with experimental estimates.

6. Key Results:

Key Results:

• The material ductility of the HPDC alloy exhibits both a global systematic variation (dependent on the casting system) and a local pseudo-random variation (due to process fluctuations).
• The local pseudo-random variation of the material ductility can be effectively described by a weakest-link Weibull distribution.
• A probabilistic failure model (MR#1) can predict the failure probability of a component from a single FE simulation, and the results are consistent with a more computationally expensive Monte-Carlo simulation (using MR#2).
• An uncoupled modeling approach (MR#3), where the material property mesh is decoupled from the FE mesh, enables mesh convergence studies for stochastic simulations, which is not possible with standard coupled approaches.
• The probabilistic model was successfully validated against three-point bending and axial compression tests on a U900-1 component, showing good correlation between predicted and experimental failure probabilities when using appropriate FE discretizations (solid or hybrid meshes).

Figure Name List:

• Figure 1.1.1: Application of two high pressure die-casting components made of the aluminium alloy Castasil-37 in the car body of the current Audi A8 (third generation (D4), production 2010 - present).
• Figure 2.0.1: Examples of casting products made of metal, concrete and plastic.
• Figure 2.1.1: Aluminium HPDC gearbox of a KTM motorcycle, see Aluminium Rheinfelden GmbH [6].
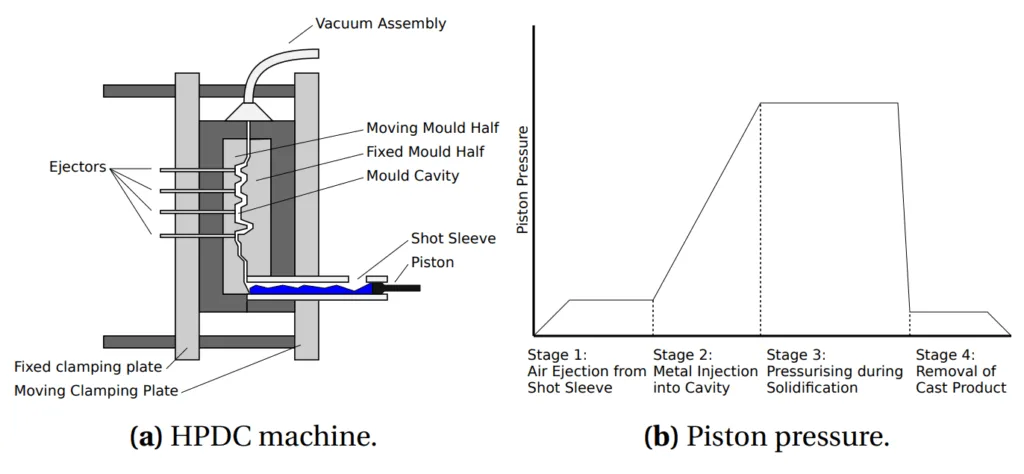
• Figure 2.1.2: Exemplary drawing of cold chamber HPDC machine with vacuum assembly and piston pressure during HPDC process.
• Figure 2.1.3: Result of an HPDC simulation preformed with MAGMAsoft, see Kleeberg [66].
• Figure 2.2.1: Characteristic phase diagrams of an Al-Si alloy and an Al-Mg alloy, see Bargel and Schulze [9].
• Figure 2.2.2: Microstructure of an HPDC Al-Si-Mg alloy, see Dørum et al. [33].
• Figure 2.3.1: Microstructure of an aluminium HPDC alloy (AlSi9Mg) containing casting defects, see Teng et al. [106].
• Figure 2.4.1: Car body of the current Audi A8 (third generation (D4), production 2010 - present): Application of aluminium sheets (green), aluminium extrusions (blue) and aluminium die-castings (red).
• Figure 3.2.1: Two events A and B taken from the sample space Ω.
• Figure 3.2.2: Bayes’ theorem.
• Figure 3.3.1: Probability Density Function (PDF) and Cumulative Distribution Function (CDF) of a discrete and a continuous random variable.
• Figure 3.3.2: Mathematical expectations and statistical measurements.
• Figure 3.3.3: Examples of uniform PDFs and CDFs (A = 1; B = 2, 4, 6).
• Figure 3.3.4: Examples of normal PDFs and CDFs (µ = 0; σ = 0.5, 1, 2).
• Figure 3.3.5: Bivariate normal distributions (σX1X2 = {0, 0.8,−0.8}).
• Figure 3.3.6: Examples of Weibull PDFs and CDFs (m = 0.5, 1, 2, 4; λ = 4).
• Figure 3.3.7: Comparison of uniform, normal and Weibull distribution with equal mean and standard deviation (µ = 3.6, σ = 1.0).
• Figure 3.3.8: Inverse transformation technique.
• Figure 3.3.9: Influence of Gaussian correlation length d0 on samples of 1D Gaussian random fields.
• Figure 3.3.10: Influence of Gaussian correlation length d0 on samples of 2D Gaussian random fields.
• Figure 3.5.1: Graphical representation of sample X and sample Y.
• Figure 3.5.2: Details of a box-plot.
• Figure 3.5.3: Distribution estimation of sample X and sample Y.
• Figure 3.6.1: Illustration of the (1 − α) · 100% confidence interval and the t-distribution.
• Figure 3.6.2: Estimated normal distribution and Weibull distribution of sample X and sample Y.
• Figure 4.1.1: Deformation measurements of a solid body.
• Figure 4.1.2: Illustration of a solid body subjected to of external loads and the Cauchy theorem.
• Figure 4.1.3: High-exponent yield surface in plane stress and two-terms Voce rule.
• Figure 4.1.4: Isotropic hypoelastic-plastic material model for metals assuming isothermal conditions.
• Figure 4.1.5: FEM applied on a structural problem.
• Figure 4.1.6: Deformation of a four node element.
• Figure 4.1.7: Discretisation of time t.
• Figure 4.1.8: Flow chart of the explicit time integration algorithm using the central differences method in the form proposed by Verlet [110].
• Figure 4.2.1: Characteristic stress-strain curves for brittle, quasi-brittle and ductile materials.
• Figure 4.2.2: Schematic representation of the fracture mechanisms in brittle and ductile materials.
• Figure 4.2.3: Stress distribution prior to fracture in a tensile test specimen.
• Figure 4.3.1: Typical specimen geometries for mechanical material tests.
• Figure 4.3.2: Schematic representation of the homogenisation procedure.
• Figure 4.3.3: Uniaxial tensile test: Tensile test set-up and experimental force elongation curves obtained from the ductile and the quasi-brittle specimen.
• Figure 4.3.4: Numerical and experimental force-elongation curves: Comparison of the three mesh sizes le = 1.00mm, le = 0.50mm and le = 0.25mm.
• Figure 4.3.5: W distributions at the moment when the elongation of the gauge section reaches the experimental rupture elongation: Comparison of the three mesh sizes le = 1.00mm, le = 0.50mm and le = 0.25mm.
• Figure 4.3.6: Influence of mesh size le on critical value Wc and averaged critical value Wc in an experimental-numerical approach.
• Figure 5.1.1: Failure probability PΛF = 1 − e−cl plotted as function of segment length l for varying weakest-link densities c.
• Figure 5.1.2: Failure probability PVF = 1 − e−c(f)V plotted as function of material volume V with a constant value of density function c(f).
• Figure 5.1.3: Failure probability by Weibull plotted as function of uniform loading f for either varying Weibull modulus m or varying volume relation V/V0.
• Figure 5.1.4: Failure probability according to the approach by Unosson et al. [108] plotted as function of loading f.
• Figure 5.1.5: Weibull plots including a Weibull curve obtained from a small gauge volume (red) and a Weibull curve obtained from a large gauge volume (blue).
• Figure 5.1.6: Gauge parts under different loading conditions with equal gauge volumes (VT = VC = VS = VPT).
• Figure 5.2.1: Randomly distributed failure parameters: The failure parameters are uniformly distributed within the FE mesh.
• Figure 5.2.2: Range of the middle 95% of a Weibull distributed population.
• Figure 5.2.3: Randomly distributed failure parameters: The failure parameters are uniformly distributed within the MS mesh, then the MS mesh is discretised into a FE mesh.
• Figure 5.2.4: Randomly distributed failure parameters: The failure parameters are distributed within the MS mesh according to a uniform random field, then the MS mesh is discretised into a FE mesh.
• Figure 7.1.1: Images of the aluminium HPDC component U900-1.
• Figure 7.2.1: Three-point bending test set-up: Technical drawing and images of the test set-up.
• Figure 7.2.2: Deformed and fractured U900-1 component subjected to three-point bending.
• Figure 7.2.3: Experimental results obtained from seven parallel three-point bending tests (measured by the testing machine).
• Figure 7.2.4: Experimental results obtained from six parallel three-point bending tests: Force and displacement measured by testing machine and relative displacements measured by extensometers on gating side and vacuum side.
• Figure 7.2.5: Drawing of the punch rotation during three-point testing.
• Figure 7.3.1: Axial compression test set-up: Cutting pattern, technical drawing and image of the test set-up.
• Figure 7.3.2: Deformed and fractured modified U900-1 component subjected to axial compression.
• Figure 7.3.3: Experimental force-displacement curves obtained from four parallel axial compression tests (measured by the testing machine).
• Figure 7.3.4: Experimental results obtained from four parallel axial compression tests: Force and displacement measured by the testing machine and relative displacement measured by the extensometer.
• Figure 7.3.5: Drawing of the loading plate rotation during axial compression testing.
• Figure 8.1.1: Technical drawing and image of the applied uniaxial tensile test set-up.
• Figure 8.1.2: Definition of U900-1 component parts (unfolded geometry).
• Figure 8.1.3: Mechanical analysis of the result obtained from a uniaxial tensile test.
• Figure 8.1.4: Mechanical analysis of the result obtained from a uniaxial tensile test.
• Figure 8.1.5: Approach of statistical hypothesis testing of k samples Xi at a significance level of α = 0.05 using MATLAB [84].
• Figure 8.2.1: Uniaxial tensile test specimen UT80 (t = 2.5mm).
• Figure 8.2.2: Engineering stress-strain curves obtained from UT80 specimens machined from an U900-1 component (component #1).
• Figure 8.2.3: Engineering stress-strain curves obtained from UT80 specimens machined from five U900-1 components presented according to the extraction position.
• Figure 8.2.4: Averages and COVs of the measured mechanical quantities obtained from UT80 specimens machined from five U900-1 components.
• Figure 8.2.5: Engineering stress-strain curves obtained from the most ductile specimen and the least ductile specimen and scatter plots of the measured mechanical quantities obtained from UT80 specimens machined from five U900-1 components.
• Figure 8.2.6: Images of fractured UT80 specimens machined from the fifteen extraction positions of the U900-1 component.
• Figure 8.2.7: Identification of casting defects in form of porosity using CT scanning of the middle section of three U900-1 components.
• Figure 8.2.8: Identification of casting defects in form of shrinkage pores, initial cracks and other microstructural irregularities using SEM of fractured UT80 specimens machined from U900-1 components.
• Figure 8.3.1: Uniaxial tensile test specimen UT75 and uniaxial tensile test specimen UT117.
• Figure 8.3.2: Engineering stress-strain curves obtained from UT75 and UT117 specimens machined from six U900-1 components presented according to extraction positions.
• Figure 8.3.3: Average and COVs of the measured mechanical quantities obtained from UT75 and UT117 specimens machined from six U900-1 components.
• Figure 8.3.4: Scatter plots of the measured mechanical quantities obtained from UT75 and UT117 specimens machined from six U900-1 components.
• Figure 8.3.5: Measured fracture strain Af obtained from UT75 and UT117 specimens machined from six U900-1 components plotted according to extraction positions in longitudinal direction.
• Figure 8.3.6: Scatter plots of the measured fracture strain Af obtained from UT75 and UT117 specimens machined from six U900-1 components.
• Figure 8.3.7: Three fractured UT117 specimens machined from part BF of U900-1 components.
• Figure 8.3.8: Probability plot of the samples based on measurements of Wc obtained from UT75 and UT117 specimens machined from part OW of six U900-1 components and extendedly fitted Weibull probability function.
• Figure 10.1.1: FE model of the uniaxial tensile test using a UT80 specimen.
• Figure 10.1.2: Fitted two-terms Voce rule based on experimental hardening curves obtained from UT80 specimens machined from part OW.
• Figure 10.1.3: Comparison of predicted engineering stress-strain curve using material routine MR#1 (red) and experimental engineering stress-strain curves (grey) as well as comparison of predicted failure probability using material routine MR#1 (blue) and experimental failure probability (blue triangles).
• Figure 10.1.4: Predicted engineering stress-strain curves using material routine MR#2 (red) and comparison of predicted failure probability using material routine MR#1 (blue) and predicted failure probability using material routine MR#2 (blue triangles).
• Figure 10.1.5: Five deformed and fractured UT80 specimens obtained from FE simulations using material routine MR#2 including the pseudo-random distributions of critical value Wc (le = 1.00mm).
• Figure 10.1.6: Mesh convergence study of the FE model of the uniaxial tensile test using material routine MR#2 (le = {1.00mm, 0.50mm, 0.25mm, 0.125mm}).
• Figure 10.1.7: Uncoupled modelling approach applied on the FE model of the UT80 specimen using material routine MR#3 and material routine MR#4.
• Figure 10.1.8: Mesh convergence study of the FE model of the uniaxial tensile test using material routine MR#3 (le = {1.00mm, 0.50mm, 0.25mm, 0.125mm}).
• Figure 10.1.9: Mesh convergence study of the FE model of the uniaxial tensile test using material routine MR#4 (le = {1.00mm, 0.50mm, 0.25mm, 0.125mm}).
• Figure 10.2.1: Image of the three-point bending test set-up and experimental results.
• Figure 10.2.2: FE model of the U-profile subjected to three-point bending.
• Figure 10.2.3: Numerical results obtained from a single simulation of the U-profile subjected to three-point bending using material routine MR#1 (le = 3.00mm).
• Figure 10.2.4: Numerical results obtained from a single simulation of the U-profile subjected to three-point bending using material routine MR#2 (le = 3.00mm).
• Figure 10.2.5: Comparison of the numerical results obtained from simulations of the U-profile subjected to three-point bending using material routines MR#1 and MR#2 (le = 3.00mm).
• Figure 10.2.6: Mesh sensitivity analysis of the FE model of the U-profile subjected to three-point bending using material routine MR#3: Predicted force-displacement curves (le = {3.00mm, 1.50mm, 0.75mm, 0.38mm}).
• Figure 10.2.7: Mesh convergence study of the FE model of the U-profile subjected to three-point bending using material routine MR#3: Prediction of fracture initiation in the vacuum side (le = {3.00mm, 1.50mm, 0.75mm, 0.38mm}).
• Figure 10.2.8: Through-process modelling approach applied on the FE model of the U-profile (le = 3.00mm).
• Figure 10.2.9: Comparison of numerical results obtained from simulations (material routine MR#1) of the U-profile subjected to three-point bending without mapping and with mapping (le = 3.00mm).
• Figure 10.3.1: Discretisation of the cross-section of the U900-1 component using a solid mesh (le ≤ 1.0mm), a shell mesh (le ≤ 8.0mm) and a hybrid mesh (le ≤ 5.0mm).
• Figure 10.3.2: FE model of the small ejector dome applied for eigenfrequency analysis and numerical results of the first bending eigenfrequency ωB1 and the first torsional eigenfrequency ωT1 (solid mesh).
• Figure 10.3.3: Part definition of the U900-1 component: Gating side (blue), intermediate part (red) and vacuum side (green).
• Figure 10.3.4: Fitted two-terms Voce rules based on experimental hardening curves obtained from UT75 specimens machined from gating side (IW), intermediate part (BF) and vacuum side (OW).
• Figure 10.3.5: Numerical model of the three-point bending test set-up.
• Figure 10.3.6: Comparison of experimental results and numerical results obtained from solid mesh, shell mesh and hybrid mesh (U900-1 component subjected to three-point bending).
• Figure 10.3.7: Numerical prediction of the cross-section deformation of the U900-1 component subjected to three-point bending using solid modelling, shell modelling and hybrid modelling.
• Figure 10.3.8: Numerical modelling of the axial compression test set-up.
• Figure 10.3.9: Comparison of experimental results and numerical results obtained from solid mesh, shell mesh and hybrid mesh (U900-1 component subjected to axial compression).
• Figure 10.3.10: Numerical prediction of the deformation of the half U900-1 component subjected to axial compression using solid modelling, shell modelling and hybrid modelling at a loading plate displacement of 7.5mm.

7. Conclusion:

The experimental work confirmed that the material ductility of the HPDC alloy exhibits a global systematic variation due to the casting system and a local pseudo-random variation due to process fluctuations. Statistical analysis showed that the U900-1 component could be separated into three characteristic parts with different ductility levels, and the local scatter could be described by a weakest-link Weibull distribution. The numerical work successfully developed and validated a probabilistic failure model. It was demonstrated that failure probability can be efficiently predicted from a single simulation (MR#1) with results consistent with a full Monte-Carlo analysis (MR#2). The use of an uncoupled modeling approach (MR#3/MR#4) was shown to be necessary to achieve mesh convergence in stochastic fracture simulations. The validated model provided a reliable prediction of failure probability for a complex component under both bending and compression loads.

8. References:

• [1] P. Abrahamsen, A Review of Gaussian Random Fields and Correlation Functions, 2nd Ed., Norwegian Computing Center, Oslo, 1997.
• [2] Aleris Switzerland GmbH, Aluminium-Gusslegierungen, Zürich, 2011.
• [3] Altair Engineering Inc: HyperMesh, http://www.altairhyperworks.com/Product,7,HyperMesh.aspx, 2014.
• [4] Aluminium Rheinfelden GmbH, Berichte aus dem Gusswerkstofftechnikum: Nicht alternde Druckgusslegierung für den Automobilbau (Castasil-37 - AlSi9Mn), Rheinfelden, 2004.
• [5] Aluminium Rheinfelden GmbH, Hüttenaluminium Druckgusslegierungen Handbuch 2007, 2nd Ed., Rheinfelden, 2007.
• [6] Aluminium Rheinfelden GmbH, Gießerbrief 27: Highlights der EUROGUSS 2008 von Aluminium Rheinfelden, Rheinfelden, 2008.
• [7] ANSYS Inc: ANSYS, http://www.ansys.com/Products/Simulation+Technology/Structural+Analysis, 2014.
• [8] Y. Bao and T. Wierzbicki, On fracture locus in the equivalent strain and stress triaxiality space, International Journal of Mechanical Sciences 46 (2004), 81 – 98.
• [9] H.J. Bargel and G. Schulze, Werkstoffkunde, 10th Ed., Springer, Berlin, 2009.
• [10] K.J. Bathe, Finite Elemente Methoden, Springer, Berlin, 2001.

Expert Q&A: Your Top Questions Answered

Q1: Why was the Cockcroft-Latham failure criterion chosen over other, more complex ductile fracture models?

A1: The Cockcroft-Latham criterion was selected for its practicality in a probabilistic framework. As detailed in Chapter 6.2, its critical value (Wc) can be calibrated from a single uniaxial tensile test. This is a significant advantage because characterizing the material's stochastic nature requires multiple repetitions of the same test to build a statistical distribution (like the Weibull distribution). Using a more complex fracture locus would require multiple different test types (e.g., shear, notched tension) for each data point, making the experimental program to establish a statistical distribution prohibitively large.

Q2: The study shows mesh convergence is an issue with standard probabilistic models (MR#2). How does the proposed uncoupled approach (MR#3) solve this?

A2: The uncoupled approach (MR#3) solves the mesh dependency issue by separating the mesh that defines the material's random properties (the Material Structure or MS mesh) from the Finite Element (FE) mesh used for the analysis. In the standard coupled approach (MR#2), the FE elements themselves define the statistical sample; refining the FE mesh changes the sample size and volume of each sample point, which alters the random field. By decoupling them, as explained in Chapter 5.2.4, the random material properties are defined on a consistent MS mesh, independent of the FE mesh refinement. This allows the FE mesh to be refined for numerical accuracy without altering the underlying statistical representation of the material.

Q3: What is the main advantage of predicting failure probability from a single simulation (MR#1) versus a full Monte-Carlo analysis (MR#2)?

A3: The primary advantage is computational efficiency. As demonstrated in the uniaxial tensile test study (Figure 10.1.4), the single simulation with MR#1 provides a failure probability curve that is well-correlated with the one estimated from 36 parallel simulations in a Monte-Carlo analysis using MR#2. This means a reliable probabilistic assessment can be achieved with the time and resources of just one simulation instead of dozens or hundreds, making the approach far more practical for industrial design cycles.

Q4: The paper mentions a global systematic variation and a local pseudo-random variation in ductility. How were these two distinct variations addressed in the final validation model?

A4: The two variations were addressed with a two-level approach in the validation model for the U900-1 component. The global systematic variation was captured by partitioning the FE model into three distinct parts—gating side (IW), intermediate part (BF), and vacuum side (OW)—based on the material characterization results. Each part was assigned a unique material card with its own specific hardening and Weibull parameters. The local pseudo-random variation within each of these parts was then captured by the probabilistic failure criterion itself (the Weibull distribution of Wc), as described in Chapter 10.3.

Q5: What was the significance of using a hybrid mesh (solid and shell elements) in the component validation, and how did it perform?

A5: The hybrid mesh was investigated as a practical compromise between the high computational cost of a full solid model and the potential inaccuracy of a full shell model. The analysis in Chapter 10.3 showed that the shell model could not capture the correct stiffness of thick features like ejector domes, leading to poor predictions. The hybrid model, however, provided a failure probability prediction (Figure 10.3.6) that was significantly better than the shell model and correlated well with both the experimental data and the full solid model, but at a much lower computational cost. This makes it a viable and attractive alternative for large-scale industrial crash simulations.

Conclusion: Paving the Way for Higher Quality and Productivity

This research provides a robust framework for overcoming one of the most significant hurdles in the design of structural HPDC components: accounting for material variability. By moving beyond simple deterministic values and embracing a Probabilistic Failure Modeling for HPDC approach, engineers can create more reliable and accurate numerical simulations. The key breakthrough—demonstrating that a component's failure probability can be accurately predicted in a single, efficient simulation—makes this advanced methodology accessible for demanding industrial timelines.

At CASTMAN, we are committed to applying the latest industry research to help our customers achieve higher productivity and quality. If the challenges discussed in this paper align with your operational goals, contact our engineering team to explore how these principles can be implemented in your components.

Copyright Information

• This content is a summary and analysis based on the paper "A Probabilistic Approach in Failure Modelling of Aluminium High Pressure Die-Castings" by "Octavian Knoll".
• Source: https://ntnuopen.ntnu.no/ntnu-xmlui/handle/11250/279899

This material is for informational purposes only. Unauthorized commercial use is prohibited.
Copyright © 2025 CASTMAN. All rights reserved.