Modelling the High Pressure Die Casting Process Using SPH

This introduction paper is based on the paper "Modelling the High Pressure Die Casting Process Using SPH" published by "CSIRO Mathematical and Information Sciences, Victoria, Australia".

1. Overview:

• Title: Modelling the High Pressure Die Casting Process Using SPH
• Author: Paul W. Cleary and Joseph Ha
• Year of publication: 2011 (October)
• Journal/academic society of publication: CRC for Cast Metals Manufacturing (CAST), CSIRO Mathematical and Information Sciences, Victoria, Australia.
• Keywords: High Pressure Die Casting (HPDC), Smoothed Particle Hydrodynamics (SPH), Numerical Modelling, Fluid Flow, Die Filling, Heat Transfer, Solidification, Free Surface Flow.

2. Abstract:

In this paper we review the progress in the SPH modelling of HPDC that has occurred over the past four years of this CAST funded project. Early examples of the filling of simple dies in two dimensions demonstrate the complexity of the flow pattern and particularly the role of free surface behaviour and breakup. The effect of the inclusion of heat transfer on the filling of these simple dies is shown, particularly the effect of the thermal boundary condition on the inside of the die and the importance of modelling the coupled conduction into the die itself. Two examples of validation using water analogue experiments are given to demonstrate the accuracy of the SPH predictions. The extension of the modelling to 3D and the methodology used to represent complex three dimensional die shapes are described. The use of this SPH system to model the filling of a realistic industrial component is presented. The importance of the order of the die filling is shown as is the role of flow separation from corners and even moderately curved surfaces. The degree of surface fragmentation, droplet formation and the strongly transient nature of the voidage are also shown. Finally the filling of the runner, gate and die for a real automotive piston head is shown and the difficulties inherent in such large scale computations are discussed.

3. Introduction:

High pressure die casting (HPDC) is a critical manufacturing process for high volume, low-cost components, particularly in the automotive industry for parts like transmission housings and piston heads. In HPDC, liquid metal (typically aluminium alloy) is injected at high speeds (around 50 to 100 m/s) and very high pressures into complex dies. The process involves strongly three-dimensional fluid flow with significant free surface fragmentation. Achieving homogeneous cast components with minimal entrapped voids depends heavily on the die filling order and gas exit positioning, which are determined by gating system design and die geometry. Improved die design, focusing on effective die filling control and thermal performance, can enhance product quality and productivity. Numerical simulation provides a powerful and cost-effective tool for studying and optimizing die designs and filling processes.

4. Summary of the study:

Background of the research topic:

HPDC is a vital industrial process characterized by high-speed, high-pressure injection of molten metal into complex dies. The intricate flow patterns, free surface fragmentation, and potential for void entrapment pose significant challenges to achieving high-quality castings. Understanding and controlling the die filling process is crucial for minimizing defects.

Status of previous research:

Eulerian methods like marker and cell (MAC) and volume of fluid (VOF) have been used for modelling interfacial flows in casting. While VOF is popular and used in commercial software (e.g., MAGMAsoft, Flow-3D), it can have difficulties with fragmentation and coalescence of complex interfaces and may suffer from numerical diffusion. Smoothed Particle Hydrodynamics (SPH), a Lagrangian particle method, is well-suited for flows with complex free surface motion, droplet formation, and splashing, as found in HPDC. SPH has advantages in modelling complex free surfaces, handling momentum-dominated flows, and implementing complicated physics like solidification and multiple phases. Previous work by the authors (Cleary, et al. 2000; Ha and Cleary, 2000) demonstrated SPH's application to 2D HPDC and favorable comparisons with water analogue experiments.

Purpose of the study:

This paper aims to review the progress made in modelling the HPDC process using SPH over a four-year CAST funded project. It also presents new results for the simulation of detailed fluid flows in a real HPDC example, demonstrating the capabilities of SPH in handling complex 3D geometries and phenomena.

Core study:

The study focuses on the application and development of the SPH method for simulating HPDC. This includes:

• SPH Methodology: Detailing the governing SPH equations for continuity, momentum, energy, and the equation of state, along with boundary conditions and numerical implementation aspects.
• 2D Numerical Studies: Simulating isothermal filling of simple die geometries (rectangular, C-shaped) to understand flow patterns, free surface behavior, fragmentation, and the effect of die, gate, or runner geometry changes.
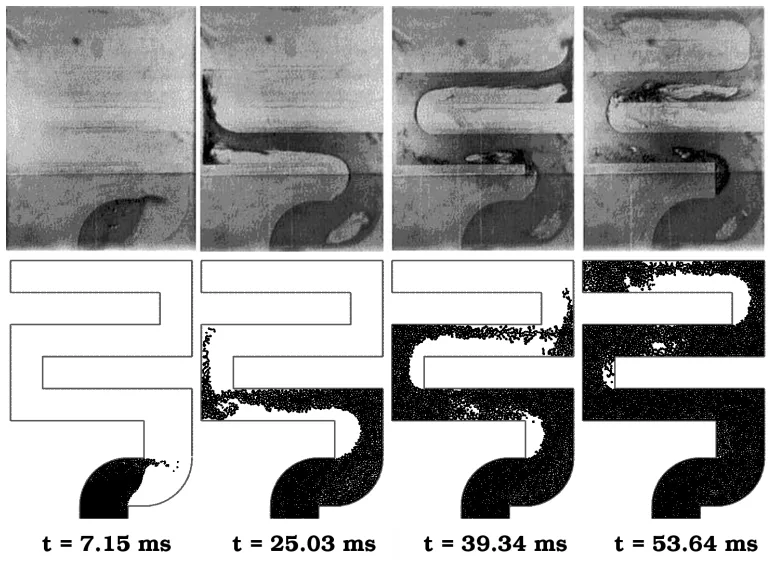
• Validation: Comparing 2D SPH simulation results with water analogue experiments for a circular disc with a core and an S-shaped cavity to assess the accuracy of SPH predictions.
• Inclusion of Heat Transfer and Solidification: Investigating the effects of heat transfer, temperature-dependent viscosity, thermal boundary conditions (isothermal vs. coupled die conduction), and latent heat release on the die filling process in a C-shaped die.
• 3D Modelling: Demonstrating the extension of SPH to model isothermal flow in complex 3D industrial components, including a generic component and a real automotive piston head, highlighting flow separation, fragmentation, and order of fill.

5. Research Methodology

Research Design:

The research employs Smoothed Particle Hydrodynamics (SPH), a Lagrangian numerical method. In SPH, the fluid is represented by a set of particles that carry physical properties (mass, temperature, density, velocity). These particles are moving interpolation points, and their motion is governed by the Navier-Stokes equations, converted into SPH form. The interpolation process uses a kernel function to smooth information from nearby particles.

Data Collection and Analysis Methods:

The SPH formulation involves:

• Continuity Equation: dρa/dt = Σb mb(va - vb) · ∇Wab (Equation 3)
• Momentum Equation: dva/dt = - Σb mb [(Pa/ρa²) + (Pb/ρb²) + Πab] ∇Wab + g (modified form of Equation 4, where Πab includes viscous terms: (ξ 4μaμb)/(ρaρb(μa+μb)) (vab·rab)/(rab²+η²))
• Equation of State: P = P₀[ (ρ/ρ₀)γ - 1 ] (Equation 5), with P₀/ρ₀ = cs² = 100V² (Equation 6) and γ=7.
• Energy Equation (Enthalpy formulation): dHa/dt = Σb 4mb(kakb)/(ρaρb(ka+kb)) (Tab rab·∇Wab)/(rab²+η²) - Σb 2mb (ξμaμb)/(ρaρb(μa+μb)) ((vab·rab)² rab·∇Wab)/((rab²+η²)²) (Equation 7), where H = ∫cp(θ)dθ + L[1-fs(T)] (Equation 8).
• Boundary Conditions: Repulsive Lennard-Jones potential force field for normal boundary forces and inclusion of boundary particles in shear force summations for non-slip conditions.
• Neighbour Search: Using a searching grid with linked lists for efficient identification of neighbouring particles.
• Initial Set-up in 3D: Obtaining geometric descriptions from CAD models, using commercial mesh generators, and an in-house pre-processor to define SPH boundary and fluid particles, their masses, and initial properties.

Simulations were conducted for various scenarios, and results were visualized through particle plots shaded by velocity, temperature, or viscosity, and rendered surface meshes for 3D flows. For validation, SPH results were compared with experimental data from water analogue experiments.

Research Topics and Scope:

The research covers several aspects of HPDC modelling:

1. 2D Isothermal Die Filling:
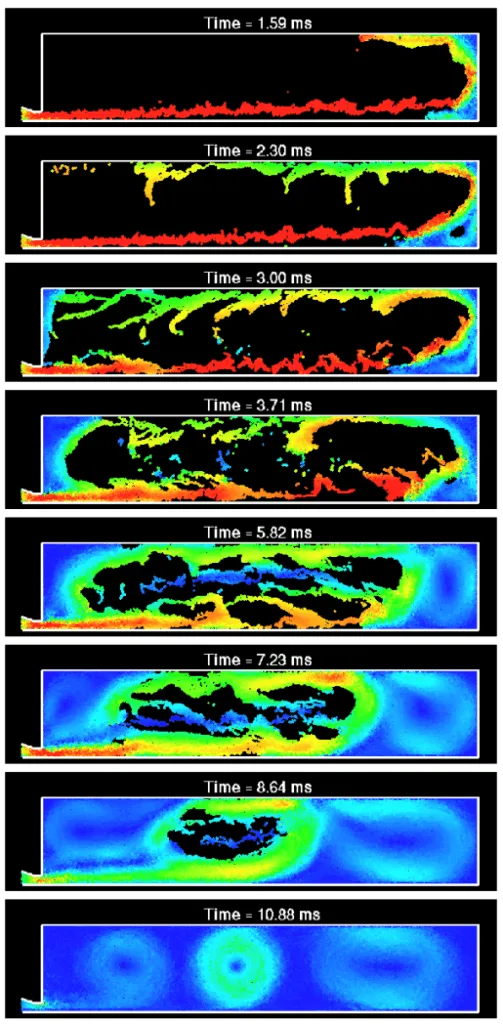
   • Filling of simple dies (short rectangular, long rectangular, C-shaped die with insert) to study flow patterns, jet behavior, fragmentation, and void formation. Reynolds numbers (Re) of 500 and 2,500 were used.
   • Effect of changes to the C-shaped die, gate, or runner geometry (inverted shot sleeve, symmetrical shot sleeve, wedged inlet) on filling patterns.
2. Validation:
   • Comparison of SPH simulations with water analogue experiments by Schmid and Klein (1995, 1998) for:
     • A circular disc with a core (die thickness 2 mm, gate velocity 18.0 m/s).
     • An S-shaped cavity (die thickness 2 mm, gate velocity 8.7 m/s).
3. Inclusion of Heat Transfer and Solidification:
   • Modelling the filling of a C-shaped die with heat transfer, using a temperature-dependent viscosity model (Thomas equation: μ= 4.5×10⁻⁶ ρm (1 + 2.5 fs + 10.05 fs² + 0.000273 exp(16.6fs))).
   • Investigating the effect of thermal boundary conditions (isothermal die walls at 27°C vs. coupled heat conduction in steel die walls with an outer temperature of 350°C).
   • Assessing the effect of latent heat release (495 kJ/kg for Al-1Cu-10Si alloy).
4. 3D Isothermal Flow Modelling:
   • Filling of a generic industrial component (slotted annular extension with cylindrical holes, ~200 mm long, 292,931 particles, Re=27,875, gate speed 44 m/s).
   • Filling of a real automotive piston head (cylindrically symmetric top, complex underside, 3 mm wide by 38 mm long gate).

6. Key Results:

Key Results:

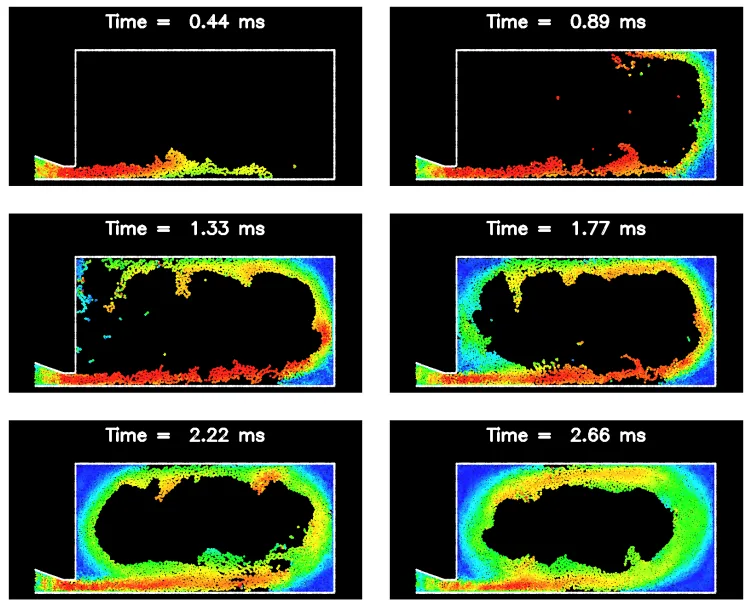
• 2D Isothermal Filling:
  • SPH simulations demonstrated complex flow patterns, including jetting, flow separation from corners, free surface fragmentation, and droplet formation even in simple 2D dies.
  • The order of fill is highly dependent on die geometry, with back-filling being common in thin wall sections.
  • Runner geometry significantly affects the fluid velocity profile at the gate and subsequent die filling.
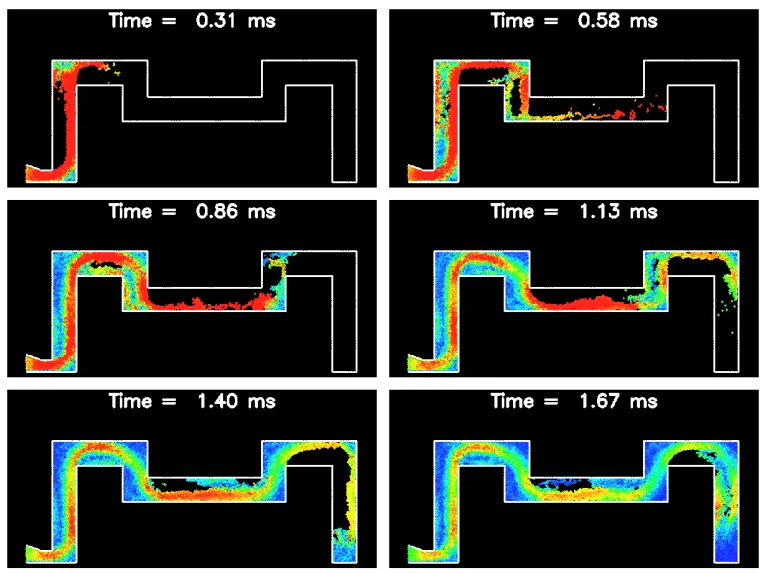
  • Changes in gate/runner design (e.g., inverted shot sleeve, wedged inlet) can modestly affect fluid distribution, with easier entry leading to more spread-out flow and potentially less complete filling of initial regions.
• Validation:
  • SPH simulations showed good agreement with water analogue experiments for both the circular disc with a core and the S-shaped cavity, capturing fine details of the flow, jet shapes, void formation, and overall filling patterns.
• Heat Transfer and Solidification:
  • Inclusion of heat transfer and solidification significantly alters filling patterns compared to isothermal cases. Solidifying material near die walls can push the free-flowing jet towards the mold center.
  • Modelling coupled heat conduction into the die is critical, as isothermal die boundary conditions remove too much heat, leading to premature solidification (cold shuts). Realistic die thermal properties limit cooling and solidification rates.
  • Latent heat release reduces the amount of predicted solidification and narrows the mushy zone, potentially leading to a 'slurry' of solidified particles in the free stream.
• 3D Isothermal Flow:
  • SPH successfully modelled complex 3D die filling, showing significant flow separation, free surface fragmentation, and transient void formation.
  • The order of fill in 3D components is complex and not necessarily based on proximity to the gate.
  • Visualization using 'virtual cameras' inside the die provided detailed insights into local flow behavior.
  • Simulations of a generic component and an automotive piston head demonstrated the capability of SPH to handle large-scale, industrially relevant problems, highlighting challenges like managing large particle counts and resolving fine geometric features.

Figure Name List:

• Figure 1: View of the shot sleeve and piston used to accelerate the metal through the gate and into the die.
• Figure 2: Filling of a short rectangular die for Re=500.
• Figure 3: Filling of a long rectangular die for Re=500.
• Figure 4: Filling of C shaped die with insert for Re=2500
• Figure 5: Fill patterns for a C shaped die with different gates at time 0.50 ms.
• Figure 6: Fill patterns for a C shaped die with different gates at time 1.50 ms.
• Figure 7: Fill patterns for a C shaped die with different gates at time 3.00 ms.
• Figure 8: Filling of the circular die with a solid core using μ= 0.001 kg/ms
• Figure 9: Filling of the S shaped die using μ= 0.001 kg/ms
• Figure 10: (a) Original input viscosity data versus (b) modified viscosity temperature relation used in the SPH simulations with a finite value of μ below T₀ representing solidified metal.
• Figure 11: Temperature distribution in the liquid metal during the filling of an isothermal C shaped die for μs/μl=100. Light grey corresponds to hot metal above the liquidus temperature and dark grey to colder metal.
• Figure 12: Viscosity distribution in the liquid metal during the filling of an isothermal C shaped die for μs/μl=100. Dark grey corresponds to low viscosity and shows liquid metal while light grey corresponds to high viscosity and represents solid metal.
• Figure 13: Viscosity distribution when the conduction in the mould is also simulated.
• Figure 14: Viscosity distribution when the conduction in the mould is also simulated and latent heat is included.
• Figure 15: Geometry of the generic 3D HPDC component.
• Figure 16: Isothermal SPH simulation of the filling of the generic component.
• Figure 17: Two perspective views of the final filled die at 14 ms.
• Figure 18: Two internal views of the filling of the generic component.
• Figure 19: Geometry of the piston head, runner and venting system.
• Figure 20: Oblique upper view of the filling of the piston head.
• Figure 21: Side view of the filling of the piston head.

7. Conclusion:

Several aspects of modelling the high pressure die casting process using Smoothed Particle Hydrodynamics have been described. Two dimensional isothermal modelling of very simple geometries demonstrated that the filling was not a uniform front fill. The order of fill was found to be strongly dependent on the die geometry with back filling being responsible for filling much of the thin wall sections. Flow separation of corners provides significant opportunities for porosity formation. The capacity of numerical simulation to easily examine the effect of changes in gate and runner geometry on filling pattern was demonstrated.

The inclusion of heat transfer and solidification via a temperature dependent viscosity were described. The importance of the choice of the die wall thermal boundary conditions was found to be particularly important with a clear necessity for modelling the coupled conduction into the die since this limits the rate of cooling and therefore of solidification. The role of latent heat release in reducing the amount of solidification predicted and in narrowing the mushy regions and allowing a slurry of solid metal to form in the free stream were examined.

Finally, the use of the SPH package to model two real complex geometry components in three dimensions was demonstrated. In each case flow separation and significant fragmentation of the free surfaces lead to large transient void formation. The importance of the order of fill of the die was confirmed for these more complex components.

8. References:

• Cleary, P.W. (1998a). SPH Technical Note #29, CSIRO Division of Mathematical and Information Sciences, Technical Report CMIS 1998/166.
• Cleary, P.W. (1998b). Applied Mathematical Modelling, 22, 981–993.
• Cleary, P.W., Ha, J., & Ahuja, V. (2000). Int. J. Cast Metals Res, 12, 335–355.
• Cleary, P.W., Ha, J., Mooney, J., & Ahuja, V. (1998). in Proc. Proc. 13th Australasian Fluid Mechanics Conference, Melbourne, Australia, 679–682.
• Cleary, P.W. & Monaghan, J. J. (1999). J. Comp. Phys., 148, 227–264.
• Cleary, P.W., Sawley, M., and Ha, J. (2001). in Proc. 5th International Workshop on Bifurcation and Localisation in Soils and Rock, Balkema.
• Gartling, D.K. (1980). in Morgan, K., Taylor, C. and Brebbia, C.A. (Eds), Computer Methods in Fluids, Pentech, London, 257-284.
• Ha, J., Cleary, P.W., Alguine, V. and Nguyen, T. (1999). in Proc. 2nd Int. Conf. on CFD in Minerals & Process Industries, Melbourne, Australia, 423-428.
• Ha, J. and Cleary, P.W. (2000). SPH Technical Note #28, CSIRO Division of Mathematical and Information Sciences, Technical Report CMIS 2000/105.
• Ha, J. and Cleary, P.W. (2000). Int. J. Cast Metals Res, 12, 409–418.
• Ha, J., Schuhmann, R., Alguine, V., Cleary, P.W. and Nguyen, T. (2000). in Proc. Modeling of Casting, Welding and Advanced Solidification Processes IX, 151–158.
• Hirt, C.W. and Nichols, B.D. (1981). J. Comp. Phys., 39, 201–225.
• Hwang, W-S, and Stoehr, R.A. (1988). Metals Handbook, Casting ASM International, 15, 867-876.
• Jai, L.R., Xiong, S.M. and Lui, B.C. (1998) in Proc. Modeling of Casting, Welding and Advanced Solidification Processes IX, Aachen, Germany, 303–310.
• Kothe, D., Brackbill, J.U. and Choi, C.K. (1990). Physics of Fluids B, 2, 1898–1906.
• Kothe, D., Juric, D., Lam, K. and Lally, B. (1998). in Proc. Modeling of Casting, Welding and Advanced Solidification Processes VIII, San Diego, California, 17–28.
• Lee, Y.C., Hwang, H.Y. and Choi, J.K. (2000). in Proc. Modeling of Casting, Welding and Advanced Solidification Processes IX, Aachen, Germany, 349–356.
• Monaghan, J. J. (1992). Ann. Rev. Astron. Astrophys., 30, 543.
• Monaghan, J. J. (1994). J. Comp. Phys., 110, 399–406.
• Morris, J.P. (2000). Int. J. Numer. Methods Fluids, 33, 333-353.
• Scheppe, F., Sahm, P.R., Hermann, W., Paul, U. and Preuhs, J. (2000). in Proc. Modeling of Casting, Welding and Advanced Solidification Processes IX, Aachen, Germany, 207–214.
• Schmid, M., and Klein F. (1995). in Proc. NADCA 18. International Die Casting Congress and Exposition, October 2-5, 1995, Indianapolis, Indiana, Paper No.I-T95-034, 93-99.
• Schmid, M. (1998). (Private Communication),
• Schmid, M. and Klein, F. (1998). in Proc. Modeling of Casting, Welding and Advanced Solidification Processes VIII, San Diego, California, 1131–1136.
• Schneider, M.C., Beckermann, C., Lipinski, D.M. and Schaefer, W. (2000). in Proc. Modeling of Casting, Welding and Advanced Solidification Processes IX, Aachen, Germany, 257–264.
• Thomas (1965). J. Colloid Science, 20, 267–277.
• Voller, V.R. and Prakash, C. (1987). Int. J. Heat Mass Transfer, 30, 1709–1719.
• Welch, J.E. and Harlow, F.H. (1966). Physics of Fluids, 9, 842-851.
• Xu, Z.A. (2000). in Proc. Modeling of Casting, Welding and Advanced Solidification Processes IX, Aachen, Germany, 312–319.

9. Copyright:

• This material is a paper by "Paul W. Cleary and Joseph Ha". Based on "Modelling the High Pressure Die Casting Process Using SPH".
• Source of the paper: https://www.researchgate.net/publication/246854585

This material is summarized based on the above paper, and unauthorized use for commercial purposes is prohibited.
Copyright © 2025 CASTMAN. All rights reserved.