A Stochastic Approach for Damage Modelling of Cast Alloys

Beyond Averages: The Future of Predictive Simulation for Cast Aluminum Alloys

This technical summary is based on the academic paper "A Stochastic Approach for Damage Modelling of Cast Alloys" by Christian Mühlstätter, published in Proceedings of 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2018) (2018).

Keywords

• Primary Keyword: Stochastic Damage Modelling
• Secondary Keywords: Cast Aluminum Alloys, Ductile Fracture Simulation, Finite Element Analysis (FEA), Material Characterization, Triaxiality, Goodness-of-fit Test

Executive Summary

• The Challenge: Conventional simulation models for cast aluminum treat material properties as uniform, failing to capture the real-world microstructural variations that lead to unpredictable component failure.
• The Method: The research combines physical testing of cast aluminum specimens under various stress states with a statistical "goodness-of-fit" test to characterize the inherent scatter in material fracture behavior.
• The Key Breakthrough: The study successfully demonstrates that the variability in fracture strain of cast aluminum can be accurately described by a normal statistical distribution, validating a stochastic (probability-based) approach to material modelling.
• The Bottom Line: By embracing material variability instead of ignoring it, stochastic damage modelling provides a path to more realistic and reliable Finite Element simulations, leading to safer, better-optimized cast components.

The Challenge: Why This Research Matters for HPDC Professionals

In the automotive industry and beyond, the demand for lightweight, high-performance components is driving the adoption of cast aluminum alloys. However, the very nature of the casting process creates a challenge. Parameters like cooling rate, pressure distribution, and melt quality introduce microstructural variations and small voids throughout the part. This results in inhomogeneous mechanical properties.

Conventional Finite Element (FE) simulation approaches treat the material as a perfect continuum, using averaged, "smoothed" data. This simplification ignores the random, spatial variation in a material's ability to resist damage. Consequently, simulations may not accurately predict when and where a real-world component will fail under stress. This discrepancy forces engineers to rely on larger safety factors, potentially leading to over-engineered, heavier, and more expensive parts. This paper addresses the critical need for a modelling concept that acknowledges and quantifies this inherent material inconsistency.

The Approach: Unpacking the Methodology

To build a more realistic model, the study first characterized the material's damage behavior under different types of stress. This was achieved by creating a foundation of robust experimental data and then applying a rigorous statistical analysis.

Method 1: Experimental Characterization of Stress States
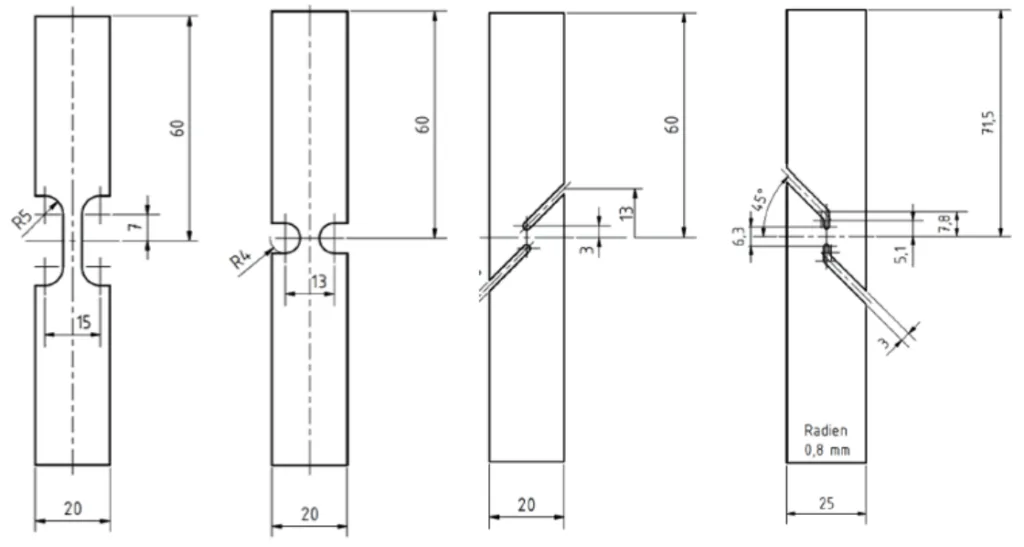
To understand how the material fails under different loading conditions, test specimens were extracted from cast hat profiles. Four distinct geometries were used to induce different levels of stress triaxiality (the ratio of hydrostatic stress to equivalent stress), which governs the mechanism of ductile fracture:
- Flat Tensile Test: Induces a triaxiality of 0.33.
- Notched Test: Creates a higher stress concentration, resulting in a triaxiality of 0.57.
- Shear Tensile & Merklein Shear Tests: Produce a triaxiality regime of 0.
These physical tests generated force-displacement curves, providing the raw data on when and how the material fractured under controlled, multi-axial stress conditions.

Method 2: Statistical Evaluation with Goodness-of-fit Test
Recognizing the scatter in the experimental results, the researchers moved beyond simple averages. They applied a statistical method called the Kolmogorov-Smirnov (KS) goodness-of-fit test. This test was used to determine if the observed random variation in the failure displacement data could be accurately described by a known statistical distribution. The null hypothesis was that the data follows a normal distribution. By analyzing the discrete failure displacement values from the experiments, this test provides a mathematical foundation for a probability-based damage model.

The Breakthrough: Key Findings & Data

The core breakthrough of this research is the successful validation of a stochastic framework for a notoriously variable material. The data clearly shows why a new approach is needed and proves the proposed statistical method is viable.

Finding 1: Experimental Data Confirms Significant Performance Scatter

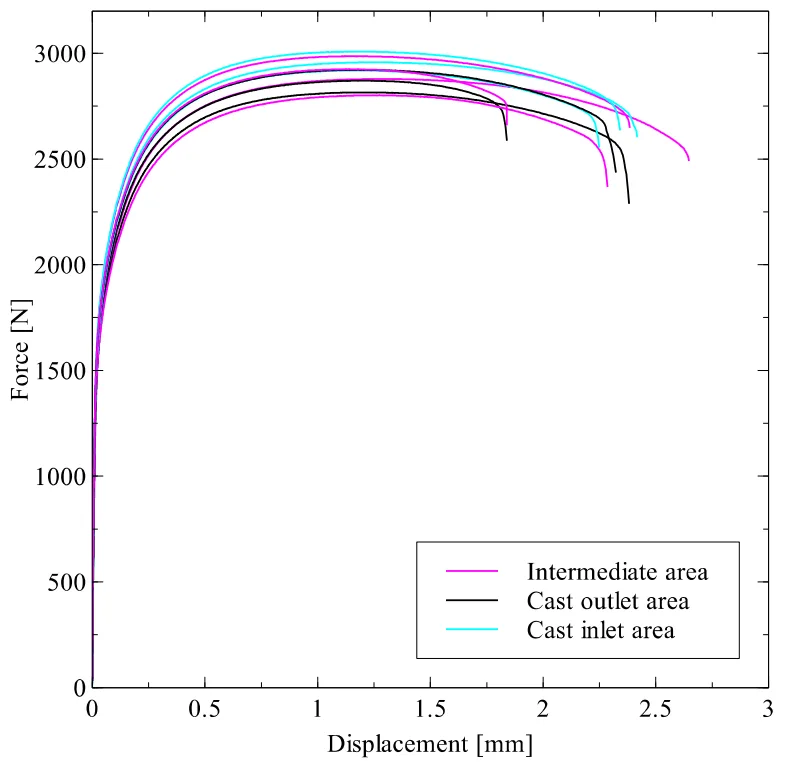
The force-displacement curves from the physical tests revealed a notable deviation in material behavior, even for specimens produced in a stable, steady-state casting process. As shown in Figure 4 for the flat tensile tests (triaxiality η = 0.33), there is a significant spread in both the ultimate force and, more importantly, the displacement at failure. A similar, though less pronounced, deviation was observed in the Merklein shear tests (Figure 5). This directly illustrates the inadequacy of using a single, averaged curve to represent the material in a simulation.

Finding 2: Fracture Strain Variability Follows a Normal Distribution

The application of the Kolmogorov-Smirnov (KS) test to the fracture strain data from the flat tensile tests yielded a critical result. The test parameter T was calculated to be 0.139, which was less than the rejection value of 0.41. This means the null hypothesis was accepted: the experimental data for fracture strain accurately follows a normal statistical distribution. Figure 6 provides a visual representation of this, showing the close match between the empirical data (black step function) and the theoretical normal distribution curve (magenta line). This confirmation is the cornerstone of the proposed stochastic model, as it provides a predictable, mathematical way to describe the material's random behavior.

Practical Implications for R&D and Operations

• For Process Engineers: This study suggests that the inherent scatter in mechanical properties is a key characteristic of the casting process. While process optimization aims to reduce variability, this stochastic approach provides a tool to realistically model the remaining, unavoidable scatter, linking it directly to component performance simulation.
• For Quality Control Teams: The data in Figure 4 and Figure 5 of the paper illustrates that relying on single-point destructive tests may not capture the full performance range of a production batch. Adopting a statistical view of material properties could inform more robust quality inspection criteria that account for expected variability.
• For Design Engineers: The findings provide a direct pathway to more reliable FEA. Instead of using a single fracture curve, the concept described in Figure 7 allows for the generation of a random field of material properties in the simulation. This means the model can account for weak spots, leading to more accurate predictions of failure initiation and a better-optimized balance between weight, cost, and safety.

Paper Details

A Stochastic Approach for Damage Modelling of Cast Alloys

1. Overview:

• Title: A Stochastic Approach for Damage Modelling of Cast Alloys
• Author: Christian Mühlstätter
• Year of publication: 2018
• Journal/academic society of publication: In Proceedings of 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2018)
• Keywords: Damage Modelling, Triaxiality, Goodness-of-fit Test.

2. Abstract:

The increasing interest of cast Aluminium alloys in structural application asks for appropriate simulation approaches. Besides the constitutive behaviour, damage properties play an important role for this material. The damage behaviour is significantly influenced by the microstructure. Due to the specific morphology of cast microstructure and the random spatial deviation of voids, a novel concept of material modelling is necessary. In this study, a concept for stochastic material characterisation and modelling in structural Finite Element simulations is introduced. Therefore, a test matrix for experimental tests is discussed. Based on the generated experimental data a stochastic evaluation is performed by a goodness-of-fit test. The achieved characterisation knowledge is used to introduce the concept for stochastic material modelling of Aluminium cast alloys.

3. Introduction:

With rising demand for lightweighting in automotive applications, cast Aluminium alloys are gaining relevance for structural parts, necessitating accurate material behaviour models for structural Finite Element (FE) simulations. The casting process imparts a characteristic morphology with voids, influenced by process parameters such as pressure distribution, cooling rate, and flow behaviour. This results in a material with varying microstructure and inhomogeneous mechanical properties. Conventional modelling approaches (e.g., Gurson, 1978; Tvergaard and Needleman, 1984) and phenomenological approaches (e.g., Wilkins, et al., 1980; Johnson and Cook, 1985) consider the material as a continuum with smoothed behaviour, describing damage via void fraction evolution or triaxiality-dependent fracture strain. However, the standard implementation of these models does not consider the spatial variation of material parameters. This paper introduces a phenomenological approach combined with a concept of stochastic consideration for cast material characterisation and modelling.

4. Summary of the study:

Background of the research topic:

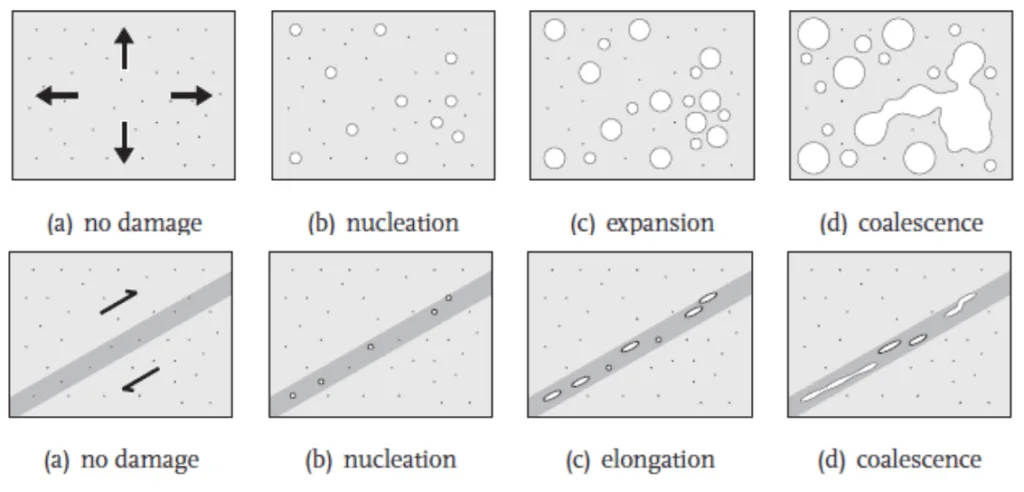
Ductile fracture in metallic materials like cast aluminum alloys is a critical characteristic for structural components. This failure mode is based on micromechanical mechanisms including the nucleation, growth, and coalescence of micro voids. The specific mechanism is highly dependent on the stress state, particularly the stress triaxiality.

Status of previous research:

Established damage models for ductile fracture include micromechanical approaches by Gurson, Tvergaard, and Needleman, which model the evolution of void fractions. Phenomenological models, such as those by Wilkins et al. and Johnson and Cook, describe material damage using a triaxiality-dependent fracture strain. The approach by Bao and Wierzbicki (2004), which defines a characteristic fracture strain as a function of stress triaxiality, is a state-of-the-art basis for damage modelling. However, these models are typically implemented with smoothed, deterministic material parameters, neglecting the inherent spatial variability in cast materials.

Purpose of the study:

The study aims to introduce a novel concept for material modelling that accounts for the stochastic nature of cast aluminum alloys. The objective is to develop a concept for stochastic material characterization and modelling to be used in structural Finite Element simulations, thereby providing a more accurate representation of real-world material behavior.

Core study:

The core of the study involves a two-part process. First, an experimental test matrix was executed using various specimen geometries (flat tensile, notched, shear tensile, Merklein shear) to characterize the material's damage behavior across a range of positive stress triaxiality values. Second, the scatter observed in the experimental force-displacement curves, specifically the failure displacement, was analyzed using a stochastic evaluation method. A goodness-of-fit test (specifically, the Kolmogorov-Smirnov test) was performed to determine if the distribution of fracture strain follows a predictable statistical pattern, such as a normal distribution. This statistical characterization forms the basis for the proposed stochastic damage modelling concept.

5. Research Methodology

Research Design:

The research was designed as an experimental and analytical study. It began with the physical testing of a cast aluminum alloy to generate baseline data on its damage behavior. This was followed by a statistical analysis of the experimental data to characterize its variability. Finally, a concept for integrating this statistical characterization into numerical simulation models was proposed.

Data Collection and Analysis Methods:

Test specimens were extracted from casted hat profiles produced by a stable die casting process. A test matrix of at least 10 valid tests for each geometry was defined. Force-displacement curves were recorded for each test. From these curves, discrete failure displacement values were extracted. The primary analysis method was the Kolmogorov-Smirnov (KS) goodness-of-fit test, which was used to compare the empirical cumulative distribution function (CDF) of the experimental fracture strain data against the CDF of a theoretical distribution (the normal distribution). Moment estimators (arithmetic mean and standard deviation) were used to define the parameters of the theoretical distribution.

Research Topics and Scope:

The research focuses on the ductile fracture behavior of cast aluminum alloys. The scope is limited to the characterization of damage under positive stress triaxiality states, as achieved through various tensile and shear tests. The study introduces a concept for stochastic modelling but does not include the full implementation and validation of this concept within an FE simulation. The analysis concentrates on the scatter of the failure displacement/fracture strain.

6. Key Results:

Key Results:

• Experimental tests on cast aluminum specimens, particularly flat tensile and notched tension tests, revealed a significant deviation and scatter in the force-displacement curves, highlighting the inhomogeneous nature of the material.
• The scatter was also apparent in Merklein shear tests, although it was lower than in the higher triaxiality regimes (η > 0.33).
• The Kolmogorov-Smirnov (KS) goodness-of-fit test was applied to the fracture strain data from the flat tensile tests.
• The test confirmed that the null hypothesis—that the test data follows a normal distribution—is true, as the condition for rejection (T ≥ 0.41) was not met (the calculated T was 0.139).
• This result provides a statistical foundation for modelling the variability of fracture strain using a normal distribution, forming the basis for the proposed stochastic damage model.

Figure Name List:

• Figure 1: Evolution of material damage by different stress states (Engelen, 2005).
• Figure 2: Characteristic metal fracture strain curve as function of the stress triaxiality (Bao and Wierzbicki, 2004).
• Figure 3: Test geometries for characterisation of the damage behaviour (from left: flat tensile, notched, shear tensile and Merklein shear).
• Figure 4: Experimental force vs. displacement curves of flat tensile tests for different regions within the casted part.
• Figure 5: Experimental force vs. displacement curves of Merklein test geometry for different regions within the casted part.
• Figure 6: Visual representation of the Kolmogorov-Smirnov goodness-of-fit test with normal distribution and empirical CDF for tensile test data.
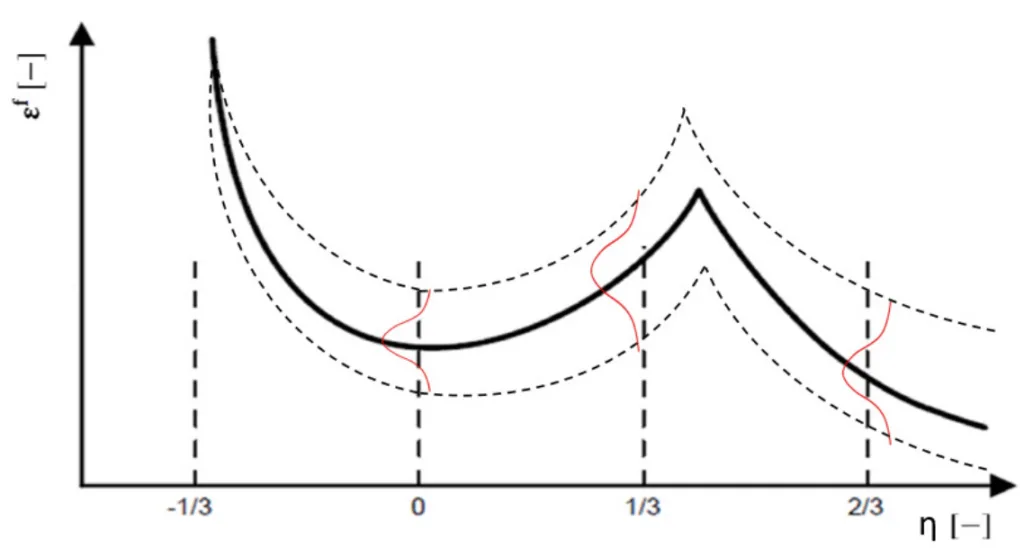
• Figure 7: Schematic concept for the stochastic damage modelling (red and dashed line) based on the approach of (Bao and Wierzbicki, 2004) (black, solid line).

7. Conclusion:

Damage modelling that considers fracture strain as a function of triaxiality is a well-established method. However, for cast aluminum alloys, the inhomogeneous material and damage behavior is typically neglected. The introduced concept of a stochastic approach can overcome this drawback. It builds a potential for more accurately capturing the material scatter of cast aluminum alloys in simulations, thereby improving the predictive capability of structural analyses.

8. References:

• Bao, Y., Wierzbicki, T., 2004. On fracture locus in the equivalent strain and stress triaxiality space. s.l.:International Journal of Mechanical Sciences.
• Engelen, R., 2005. Plasitcity induced Damage in Metals: nonlocal modelling at finite strains. s.l.:Habilitation thesis.
• Fagerholt, E.; et al., 2010. Experimental and numerical investigation of fracture in a cast aluminium alloy. s.l.:International Journal of Solids and Structures.
• Gurson, A. L., 1978. Porous rigid-plastic materials containing rigid inclusions-yield function, plastic potential and void nucleation. s.l.:The Physical Metallurgy of Fracture.
• Johnson, G. R., Cook, W. H., 1985. Fracture characteristics of three metals subjected to various strains, strain rates, terperatures and pressures. s.l.:Engineering Fracture Mechanics.
• Muehlstaetter, C., 2015. Versagensmodellierung von Al-Gusswerkstoffen. s.l.:Master Thesis, Upper Austrian University of applied sciences.
• Muehlstaetter, C., Hartmann, M., 2016. Material modelling of cast Aluminium by application of the Wilkins Damage Model. s.l.:ECCOMAS Congress Proceedia.
• Schiefermayr, K., Weiß, P., 2014. Wahrscheinlichkeits-rechnung und Statistik. s.l.:Course book, Upper Austrian University of applied sciences.
• Tvergaard, V., Needleman, A., 1984. An analysis of ductile rupture in notched bars. s.l.:Journal of the Mechanics and Physics of Solids.
• Wilkins, M. L., Streit, R. D., Reaugh, J. E., 1980. Cumulative-strain-damage model of ductile fracture: Simulation and prediction of engineering fracture tests. s.l.:s.n.

Expert Q&A: Your Top Questions Answered

Q1: Why was the Kolmogorov-Smirnov (KS) test specifically chosen for this analysis?

A1: The paper states that the KS test was selected because it "delivers accurate results for low data." In many industrial R&D settings, generating a very large dataset for statistical analysis can be time-consuming and expensive. The suitability of the KS test for smaller sample sizes makes this approach more practical and accessible for characterizing production materials.

Q2: The study focuses on positive triaxiality. How would this stochastic concept apply to compressive stress states?

A2: The paper explicitly acknowledges this limitation, stating, "The negative triaxiality regime cannot be covered with this characterisation strategy." The test geometries used (tensile, shear) are designed to probe ductile fracture mechanisms. Different mechanisms dominate under high compression, which would require a separate set of experiments and potentially a different statistical modelling approach.

Q3: How is this stochastic concept practically implemented in a Finite Element simulation?

A3: The paper proposes a conceptual framework depicted in Figure 7. The idea is to use the statistically validated probability functions (like the normal distribution curve shown) as input for a random variable generator within the simulation software. This generator would then assign a unique fracture strain curve to each integration point (or element) in the model, creating a "random field" of material properties that statistically mirrors the real-world cast component.

Q4: Does the location within the casting (e.g., near the gate vs. a remote area) influence the results?

A4: Yes, and the methodology accounts for this. The paper notes that test specimens were extracted from different spatial locations, including the "cast inlet area" and "cast outlet area," as shown in the legends of Figures 4 and 5. By documenting and testing samples from various regions, the study captures the overall spatial variability, which is precisely the phenomenon the stochastic model aims to represent.

Q5: What is the main advantage of this stochastic model over simply using a lower-bound material curve for a conservative design?

A5: Using a single lower-bound curve is a conservative but potentially inefficient approach. It assumes the entire component is made of the "worst-case" material, which can lead to over-engineering, excess weight, and higher cost. The stochastic approach provides a more realistic simulation of failure, which is often a local event. It can predict the probability of failure, allowing for a more nuanced, reliability-based design that better optimizes the trade-off between safety and performance.

Conclusion: Paving the Way for Higher Quality and Productivity

The fundamental challenge with cast aluminum alloys is their inherent variability. This research presents a clear and logical path forward. By ceasing to treat material scatter as a nuisance to be averaged away and instead characterizing it with robust statistical tools, we can unlock a new level of predictive accuracy. The validation of Stochastic Damage Modelling provides engineers with a powerful concept to create FE simulations that behave more like their real-world counterparts. This leads to better-optimized designs, increased confidence in performance predictions, and a reduction in costly over-engineering.

"At CASTMAN, we are committed to applying the latest industry research to help our customers achieve higher productivity and quality. If the challenges discussed in this paper align with your operational goals, contact our engineering team to explore how these principles can be implemented in your components."

Copyright Information

This content is a summary and analysis based on the paper "A Stochastic Approach for Damage Modelling of Cast Alloys" by "Christian Mühlstätter".

Source: https://doi.org/10.5220/0006909904670471

This material is for informational purposes only. Unauthorized commercial use is prohibited.
Copyright © 2025 CASTMAN. All rights reserved.