This technical summary is based on the academic paper "OPTIMIZATION OF CASTING PROCESS BASED ON BOX BEHNKEN DESIGN AND RESPONSE SURFACE METHODOLOGY" by Rathish Raghupathy and K.S. Amirthagadeswaran, published in the International Journal for Quality Research (2014). It has been analyzed and summarized for technical experts by CASTMAN.
Keywords
- Primary Keyword: Casting Process Optimization
- Secondary Keywords: Box-Behnken Design, Response Surface Methodology, Casting Defect Reduction, Grey Cast Iron Casting, Foundry Process Control
Executive Summary
- The Challenge: High defect rates, particularly blow-holes, in grey cast iron components were causing significant quality losses and production inefficiencies.
- The Method: A Box-Behnken Design of Experiments (DOE) and Response Surface Methodology (RSM) were used to systematically analyze the impact of three key process parameters—Clay percentage, Moisture percentage, and Mold hardness—on casting quality.
- The Key Breakthrough: The study developed a precise mathematical model that identified optimal process settings, and confirmation trials using these settings successfully produced 100% defect-free castings.
- The Bottom Line: A systematic, data-driven approach to controlling sand molding parameters is essential for minimizing defects, improving casting quality, and achieving consistent production outcomes.
The Challenge: Why This Research Matters for HPDC Professionals
In any foundry, consistent quality is paramount. For manufacturers of grey cast iron components, defects are a persistent challenge that directly impacts yield, cost, and customer satisfaction. This research was initiated to address a critical quality issue in the production of pump adapter castings.
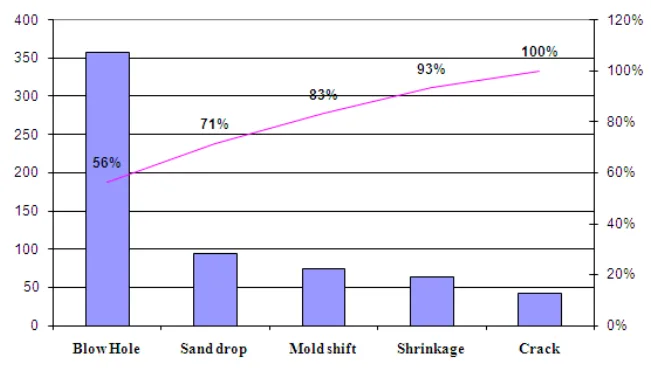
Based on a Pareto analysis of six months of production data, the study identified the "blow-hole" defect as the primary cause of quality loss, recurring far more frequently than other issues like sand drops, mold shifts, or shrinkage (Figure 1). The root cause was traced back to variations in the bonding strength of the molding sand, which is controlled by a delicate balance of sand, clay, and water. The core challenge was to move beyond trial-and-error and establish a scientifically optimized, repeatable process window that would produce sound, defect-free castings every time.
The Approach: Unpacking the Methodology
To solve this challenge, the researchers employed a powerful statistical technique known as Response Surface Methodology (RSM) with a Box-Behnken Design (BBD) of experiments. This approach allows for an efficient and comprehensive analysis of how multiple factors and their interactions affect a final outcome.
The study focused on three dominant process parameters identified from an Ishikawa (fishbone) diagram:
1. Clay Percentage (A): Varied between 2% and 4%.
2. Moisture Percentage (B): Varied between 3% and 5%.
3. Mold Hardness (C): Varied between 5 and 6 kg/cm².
A 15-run experimental matrix was generated using Design-Expert® software. For each run, ten pump adapter castings were produced, and the percentage of defective components was measured as the key response. This systematic design allowed the researchers to not only study the individual effect of each parameter but also to understand the crucial interactions between them, ultimately leading to a robust predictive model for casting quality.
The Breakthrough: Key Findings & Data
The experimental results provided clear, actionable insights into controlling the casting process. The Analysis of Variance (ANOVA) was instrumental in identifying the most significant factors.
Finding 1: Clay and Mold Hardness are the Dominant Factors
The ANOVA results, detailed in Table 3, revealed that Clay percentage (A) and Mold Hardness (C) were the most statistically significant factors influencing the rate of defects. Both parameters showed a p-value of 0.0060, indicating a high level of confidence (95%) in their impact. Interestingly, the main effect of Moisture percentage (B) was found to be not statistically significant (p-value = 0.1275), though its interaction with mold hardness (BC) was significant. This highlights that focusing control efforts primarily on clay and mold hardness offers the greatest leverage for quality improvement.
Finding 2: A Predictive Model for Defect Reduction
The research successfully developed a second-order polynomial equation (Equation 3) that accurately models the relationship between the input parameters and the percentage of defective castings. The model's high R-Squared value of 0.9592 indicates that it explains nearly 96% of the variability in the results, confirming a strong correlation between the experimental data and the predicted values. This mathematical model serves as a powerful tool for predicting casting quality based on specific process settings before production begins.
Finding 3: Confirmation of Defect-Free Production
Using the predictive model, the researchers performed a numerical optimization to find the ideal process settings for minimizing defects. The optimal conditions were identified as:
* Clay: 2%
* Moisture: 3.87 - 4.00%
* Mold Hardness: 5.21 - 5.45 kg/cm²
To validate this, a series of 10 confirmation experiments were conducted, producing a total of 30 pump adapter castings. Upon inspection, all 30 castings were found to be defect-free, raising the approved casting rate from an existing 58.7% to 100%. This provided definitive proof that the optimized parameters achieved the desired outcome.
Practical Implications for R&D and Operations
- For Process Engineers: This study suggests that adjusting clay percentage and mold hardness may contribute to significantly reducing blow-hole defects. The optimal ranges provided in Table 6 offer a validated starting point for process stabilization and improvement.
- For Quality Control Teams: The data in the ANOVA table (Table 3) and the perturbation plot (Figure 5) of the paper illustrates the high sensitivity of defect rates to variations in clay and mold hardness. This could inform new, stricter in-process quality inspection criteria for sand preparation and mold making.
- For Design Engineers: The findings indicate that process parameter stability is critical to achieving a quality casting. This reinforces the need for close collaboration between design and manufacturing to ensure component designs are robust and can be consistently produced within an optimized process window.
Paper Details
OPTIMIZATION OF CASTING PROCESS BASED ON BOX BEHNKEN DESIGN AND RESPONSE SURFACE METHODOLOGY
1. Overview:
- Title: OPTIMIZATION OF CASTING PROCESS BASED ON BOX BEHNKEN DESIGN AND RESPONSE SURFACE METHODOLOGY
- Author: Rathish Raghupathy, K.S. Amirthagadeswaran
- Year of publication: 2014
- Journal/academic society of publication: International Journal for Quality Research 8(4) 569–582
- Keywords: Design of Experiments, Box-Behnken Design, Response surface methodology, Analysis of Variance (ANOVA), Optimization
2. Abstract:
Sound and accurate castings reveal the quality of a foundry unit. In this case study, an attempt has been made to optimize the production of grey cast pump adapter castings using Box - Behnken design of experiments (DOE) approach in a foundry producing grey cast iron components. Process parameters like Clay percentage, Moisture percentage and Mold hardness were found to be dominant factors to control during the production process. Three different levels of each factor were considered for experimentation using BBD. Experimental trials were conducted using the design matrix and response in each experiment was measured and the results were tabulated. Design Expert software was used to analyse and optimize process parameters for confirmatory experiments. Analysis of Variance (ANOVA) test was conducted to identify significant parameters. The parametrical settings of the confirmatory experiments produced defect free pump adapter castings. The effects of variation of the process parameters and their influence on the quality of the castings were discussed. The research concluded that careful adjustment of process parameters is necessary since bonding strength is directly related to these parameters; in turn have an effect on the quality of castings produced.
3. Introduction:
Most of the automotive and allied components in today's world are produced by metal casting. Sand casting is the oldest method of producing castings in which a molten metal is poured into the mold cavity made of sand. The essential components of sand casting process are sand (Silica, SiO₂), clay such as Bentonite, and water. The silica sand is bonded with clay and water to mold the sand. The silica sand can be used for number of times but each and every time, it is required to add clay and water in a sufficient amount to aid bonding strength. Variation in bonding strength of sand would produce defects in castings. Optimal settings can be defined as the best level of process parameters that would produce the desired response. Optimal settings can be obtained with the parameters like green strength, moisture content, permeability and mold hardness.
4. Summary of the study:
Background of the research topic:
The study focuses on sand casting, a fundamental method for producing automotive and other industrial components. The quality of these castings is highly dependent on the properties of the molding sand, which are determined by the mixture of sand, clay (Bentonite), and water. Variations in these components can lead to defects, impacting the final product quality.
Status of previous research:
The paper acknowledges numerous research works on casting process optimization using methods like Taguchi's orthogonal array, Artificial Neural Networks, and computer simulations. It notes that while these methods are effective, the present study provides specific insight into the use of Box-Behnken Design and Response Surface Methodology for eliminating defects in iron sand casting.
Purpose of the study:
The primary purpose was to optimize the production process of grey cast iron pump adapter castings to minimize defects. The study aimed to identify the most influential process parameters, develop an empirical model to predict casting quality, and determine the optimal settings to produce defect-free components.
Core study:
The core of the study involved using a Box-Behnken Design of Experiments to investigate the effects of three factors—Clay percentage, Moisture percentage, and Mold hardness—on the percentage of defective castings. The results were analyzed using ANOVA and Response Surface Methodology to create a predictive model and find the optimal process window. The findings were then validated through confirmatory experiments.
5. Research Methodology
Research Design:
The study used a Box-Behnken Design (BBD), which is a type of response surface methodology (RSM) design. BBD is an efficient, rotatable second-order design based on three-level incomplete factorial designs. For this study with three factors, a 15-run design matrix was generated.
Data Collection and Analysis Methods:
Data was collected by conducting 15 sets of experimental trials based on the BBD matrix. For each trial, ten castings were produced, and the response (percentage of defective components) was measured through visual inspection. The collected data was analyzed using Design-Expert® V7 software. Analysis of Variance (ANOVA) was performed to test the statistical significance of the model and its terms.
Research Topics and Scope:
The research was focused on the green sand casting process for producing grey cast iron pump adapter castings. The scope was limited to three key process parameters: Clay percentage (2-4%), Moisture percentage (3-5%), and Mold hardness (5-6 kg/cm²). The primary response variable was the percentage of defective castings.
6. Key Results:
Key Results:
- A Pareto analysis identified "blow-hole" as the most significant defect in the existing production process.
- ANOVA results showed that Clay percentage and Mold Hardness are the most statistically significant parameters affecting casting defects (p=0.0060 for both).
- A second-order polynomial model was developed that accurately predicts the percentage of defects with a high R-Squared value of 0.9592.
- The optimal process parameters were determined to be: Clay 2%, Moisture 3.87-4%, and Mold Hardness 5.21-5.45 kg/cm².
- Confirmation experiments conducted with the optimal settings resulted in a 100% yield of defect-free castings, a significant improvement from the previous 58.7% approval rate.
Figure Name List:
- Figure 1. Pareto analysis of defects in castings
- Figure 2. Ishikawa Diagram for Casting defect analysis
- Figure 3. Normal probability plot of residuals for Defective percentage
- Figure 4. Residuals versus Predicted for Defective percentage
- Figure 5. Perturbation plot of defective percentage data
- Figure 6. Predicted versus Actual responses
- Figure 7. 3D surface graph of Clay versus Mold Hardness
- Figure 8. Contour plot of Clay versus Mold hardness
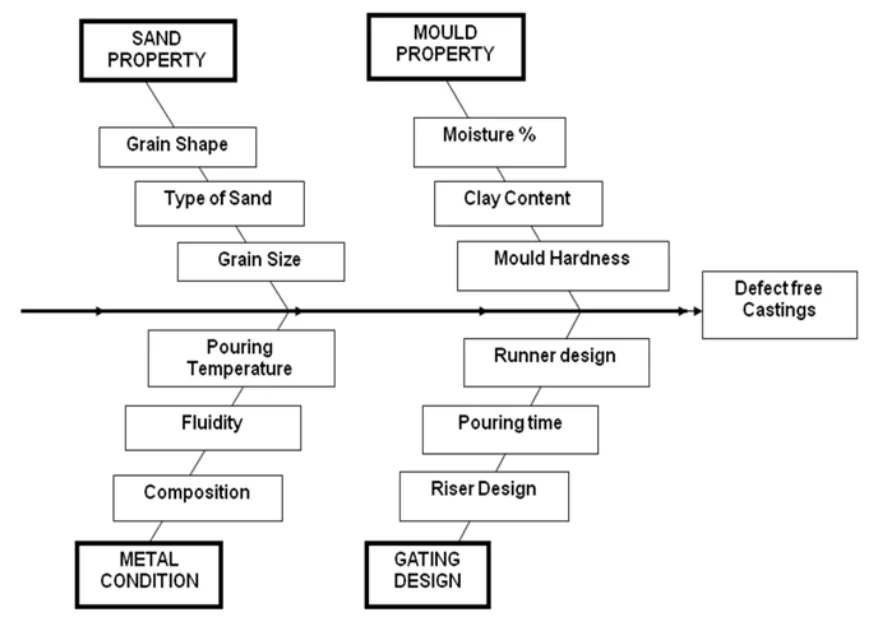
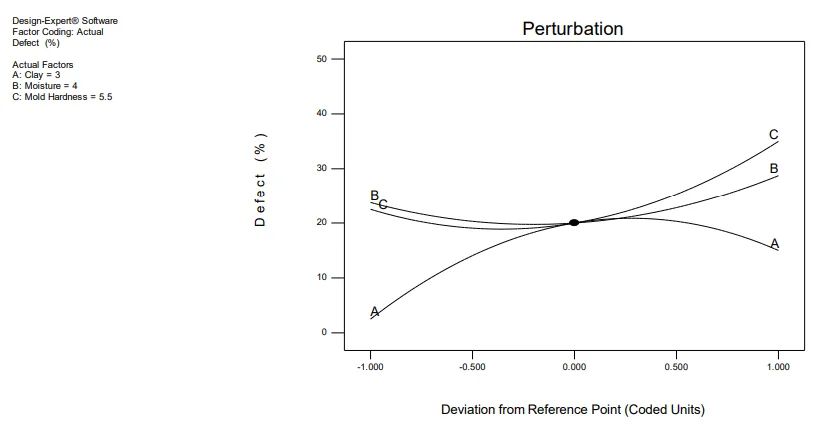
7. Conclusion:
The study successfully demonstrated that the Box-Behnken design of experiments is an effective method for optimizing the sand casting process. The F-Test from the ANOVA revealed that the proportions of clay and mold hardness were equally significant and critical parameters in controlling defects. By carefully adjusting these process parameters to the optimized settings (Clay 2%, Moisture 3.87-4%, Mold Hardness 5.21-5.45 kg/cm²), the foundry was able to produce defect-free pump adapter castings. The research concluded that careful, data-driven adjustment of process parameters is necessary to control bonding strength and, in turn, the quality of castings produced.
8. References:
- Anderson S.S., dos Santos Walter N.L. (2005). Ferreira Se'rgio LC. Application of Box-Behnken design in the optimization of an on-line pre-concentration system using knotted reactor for cadmium determination by flame atomic absorption spectrometry. Spectrochimica Acta Part B 609, 737-42.
- Anderson, M.J., Whitcomb, P.J. (2005). RSM Simplified: Optimizing Process Using Response Surface Methods for Design of Experiments. Productivity Press, New York.
- Awaj, Y.M., Singh, A.P., & Amedie, W.Y. (2013). Quality improvement using statistical process control tools in glass bottles manufacturing company, International Journal for Quality research, 7(4), 107- 126.
- Box, G.E.P., & Benhken, D.W. (1960). Technometrics, 2, 195.
- Box, G.E.P., Hunter, W.G., & Hunter, J.S. (1978). Statistics for experimenters. New York: Wiley.
- Dabade U.A., & Bhedasgaonkar, R.C. (2013). Casting Defect Analysis using Design of Experiments (DoE) and Computer Aided Casting Simulation Technique, Forty Sixth CIRP Conference on Manufacturing Systems, Procedia CIRP 00 (2013) 000–000.
- Guharaja, S., Noorul, H.A., & Karuppannan, K.M. (2006). Optimization of green sand casting process parameters by using Taguchi's method. International Journal of Advanced Manufacturing Technology, 30, 1040–1048.
- Gunaraj, V., & Murugan, N. (1999). Application of response surface methodologies for predicting weld base quality in submerged arc welding of pipes. Journal of Material Processing Technology, 88, 266–75.
- Kandananond, K. (2013). The application of Box-behnken method to optimize the design of EWMA chart for autocorrelated processes, International Journal for Quality research 7(2), 175-186.
- Karunakar, D.B., & Datta, G.L. (2003). Modelling of green sand mold parameters using artificial neural networks, Indian Foundry Journal, 49(12), 27–36.
- Karunakar, D.B., & Datta, G.L. (2007). Controlling green sand mold properties using artificial neural networks and genetic algorithms-a comparison. Applied Clay Science 37 (1–2), 58– 66.
- Kumar, A., & Singh, J. (2011). Optimization of Sand Casting Process Parameters for Ferrous Material by using Design of Experiments, International Journal of Emerging Technologies 2(2), ISSN: 0975-8364, 122-127.
- Kundu, R.R., & Lahiri, B.N. (2008). Study and statistical modelling of green sand mold properties using RSM, International Journal of Materials and Product Technology, 31 (2/3/4), 143-158.
- Kwak, J.S. (2005). Application of Taguchi and response surface methodologies for geometric error in surface grinding process. International Journal of Machine Tools Manufacturing, 45, 327-34.
- Lakshmanan, S. (2010). Improving Quality of Sand Casting using Taguchi Method and ANN analysis, International Journal on Design and Manufacturing Technologies, 4(1).
- Makino, H., Hirata, M., & Hadano, Y. (2003). Computer simulation and optimization of sand filling using the distinct element method. WFO Technical Forum.
- Montgomery, C.D. (2001). Design and analysis of experiments. Singapore: John Wiley and Sons, Pte. Ltd.
- Myers, R.H., & Montgomery, D.C. (2002). Response Surface Methodology Process and Product Optimization Using Designed Experiments, 2nd ed, Wiley Interscience, New York.
- Nekere, M.L., & Singh, A.P. (2012). Optimization of Aluminium blank sand casting process by using Taguchi's Robust design method, International Journal for Quality research, 6(1).
- Saikaew, C., & Wiengwiset, S. (2012). Optimization of molding sand composition for quality improvement of iron castings, Applied Clay Science, 67-68, 26-31
- Scheffé, H. (1958). Experiments with mixtures. Journal of Royal Statistical Society Series B(20), 344-366.
- StatEase, (2005). Inc., Design Expert 7 User's Guide, Minneapolis.
- Tegegne, A., & Singh, A.P. (2013). Experimental Analysis and Ishikawa diagram for Burn on Effect on Manganese silicon alloy medium carbon steel shaft, International Journal for Quality research, 7(4), 545-558.
- Telford, J.K. (2007). A Brief introduction to Design of Experiments, Johns Hopkins APL Technical Digest, 27(3).
- Upadhye, R.A. (2012). Optimization of Sand Casting Process parameter using Taguchi Method in Foundry, International Journal of Engineering Research & Technology, 1(7), ISSN: 2278-0181.
Expert Q&A: Your Top Questions Answered
Q1: Why was the Box-Behnken Design (BBD) chosen for this experiment over other methods?
A1: The paper states that the Box-Behnken design is an efficient method for fitting second-order polynomials, which are used to model the curvature in a response. It requires fewer experimental runs than central composite designs for the same number of factors. This makes it a cost-effective and time-efficient choice for optimizing processes where interactions between variables are expected to be important.
Q2: The ANOVA table (Table 3) shows moisture percentage isn't statistically significant on its own, yet it's part of the final optimized settings. Why is it still important?
A2: While the main effect of moisture (Factor B) was not statistically significant (p=0.1275), the ANOVA table shows that the interaction between moisture and mold hardness (BC) was significant (p=0.0493). This means that the effect of moisture on defects depends on the level of mold hardness, and vice-versa. Therefore, it must be controlled within a specific range in conjunction with the other parameters to achieve the optimal, low-defect outcome.
Q3: What does the "Adeq. Precision" value of 14.626 in Table 4 signify for this model?
A3: According to the paper, "Adeq. Precision" measures the signal-to-noise ratio, and a ratio greater than 4 is considered desirable. The obtained value of 14.626 is significantly higher than 4, which indicates an adequate signal. This confirms that the model has enough discrimination power and can be reliably used to navigate the design space to find optimal process settings.
Q4: How did the researchers determine that "blow-hole" was the most critical defect to focus on?
A4: The researchers used a Pareto analysis, a fundamental quality control tool. They analyzed six months of production data for the pump adapter castings to identify the most frequently occurring defects. As shown in Figure 1, the Pareto chart clearly revealed that the blow-hole defect was the key issue that recurred most often and accounted for the largest loss in quality.
Q5: What specific steps were taken to validate the accuracy and reliability of the final optimized settings?
A5: The study performed crucial validation through confirmation experiments. After numerical optimization identified the ideal process window, the researchers ran a set of 10 confirmation experiments three times, producing a total of 30 castings using these optimal settings. On inspecting all 30 samples, they were all found to be defect-free. This real-world validation confirmed that the model's predictions were accurate and the optimized parameters were effective.
Conclusion: Paving the Way for Higher Quality and Productivity
This research provides a clear roadmap for tackling persistent quality issues in the foundry. By moving away from reactive problem-solving to a proactive, data-driven methodology, the study successfully eliminated a major defect and achieved 100% quality yield. The core lesson is the power of systematic Casting Process Optimization. By using tools like Box-Behnken Design and Response Surface Methodology, engineers can gain deep insights into the complex interactions between process variables and develop a robust, repeatable manufacturing window.
At CASTMAN, we are committed to applying the latest industry research to help our customers achieve higher productivity and quality. If the challenges discussed in this paper align with your operational goals, contact our engineering team to explore how these principles can be implemented in your components.
Copyright Information
- This content is a summary and analysis based on the paper "OPTIMIZATION OF CASTING PROCESS BASED ON BOX BEHNKEN DESIGN AND RESPONSE SURFACE METHODOLOGY" by "Rathish Raghupathy and K.S. Amirthagadeswaran".
- Source: International Journal for Quality Research 8(4) 569–582, ISSN 1800-6450
This material is for informational purposes only. Unauthorized commercial use is prohibited.
Copyright © 2025 CASTMAN. All rights reserved.