GATING DESIGN CRITERIA FOR SOUND CASTING

This introductory paper is the research content of the paper "GATING DESIGN CRITERIA FOR SOUND CASTING" published by IJMERR.

Figure 2: Illustration of Bernoulli's Theorem (Sylvia J G, 1972)

1. Overview:

Title: GATING DESIGN CRITERIA FOR SOUND CASTING
Author: Mazhar Iqbal
Publication Year: 2014
Publishing Journal/Academic Society: International Journal of Mechanical Engineering and Robotics Research (IJMERR)
Keywords: Gating system, sprue, runner, ingates, shrinkage,

2. Abstracts / Introduction

Casting may experience defects such as porosity and incomplete filling. Gating/riser system design is critical to improving casting quality. The objective of the research is to optimize gating systems with the goal of improving casting quality such as reducing incomplete filling area, decreasing large porosity and increasing yield.

3. Research Background:

Background of the Research Topic:

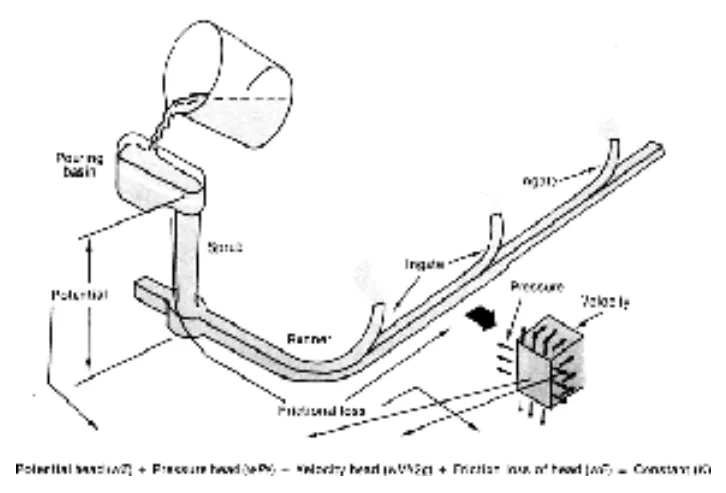
The gating system is the network of channels that delivers molten metal to the mold cavity. It includes elements like the pouring basin, sprue, sprue base well, runner, runner extension, and in-gate (Rao PN, XXXX).

Status of Existing Research:

Design variables often conflict, requiring compromises based on specific casting, molding, and pouring conditions (Wallace J F and Evans E B, 1959; Sylvia J G, 1972).

Necessity of the Research:

Proper gating system design is crucial for achieving defect-free castings, necessitating a systematic approach to address the various requirements.

4. Research Purpose and Research Questions:

Research Purpose:

To optimize gating systems to improve casting quality.

Key Research:

Reducing incomplete filling, decreasing porosity, and increasing yield.

5. Research Methodology

Research Design:

The methodology is based on a review of fundamental fluid flow principles and established design considerations.

Data Collection Method:

The data collection relies on existing literature and established foundry practices.

Analysis Method:

The analysis utilizes established fluid dynamics principles such as Bernoulli's Theorem and the Law of Continuity.

Research Subjects and Scope:

The research focuses on the principles of gating system design applicable to various casting processes.

6. Main Research Results:

Key Research Results:

The paper presents a comprehensive overview of gating system design principles and considerations.

Analysis of presented data:

Fluid Flow Principles: Bernoulli's Theorem (Eq 1), the Law of Continuity (Eq 2), and Reynolds's Number (Eq 3) are presented to explain fluid flow in gating systems.
Design Variables: Methods to achieve rapid mold filling, minimize turbulence, avoid mold and core erosion, remove slag/dross/inclusions, promote favorable thermal gradients, maximize yield, economical gating removal, avoid casting distortion, and compatibility with existing molding/pouring methods are discussed.
Gating System Types and Layout: Horizontal and vertical gating systems, as well as top, parting, and bottom gating, are described, along with their respective applications. Gating channel layout considerations, such as the number and location of ingates, are also discussed.
Mould Filling Phenomenon: Fluidity, Metallostatic Head, Viscosity, Surface Tension, Heat Diffusivity, Back Pressure, Friction, and Turbulence.
Optimal Filling Time: A generalized equation for filling time is introduced.
Gating Element Design: Design considerations for the sprue, sprue well, runner, and ingate are presented. A flow chart for gating element design is provided (Figure 10).
Optimization and Validation: Criteria for assessing gating design, including mold filling time, ingate velocity, impingement, gating yield, and fettling, are discussed. Various validation techniques, such as shop floor trials, high-speed radiography, partial filling, open mold studies, and contact wire sensing, are summarized.

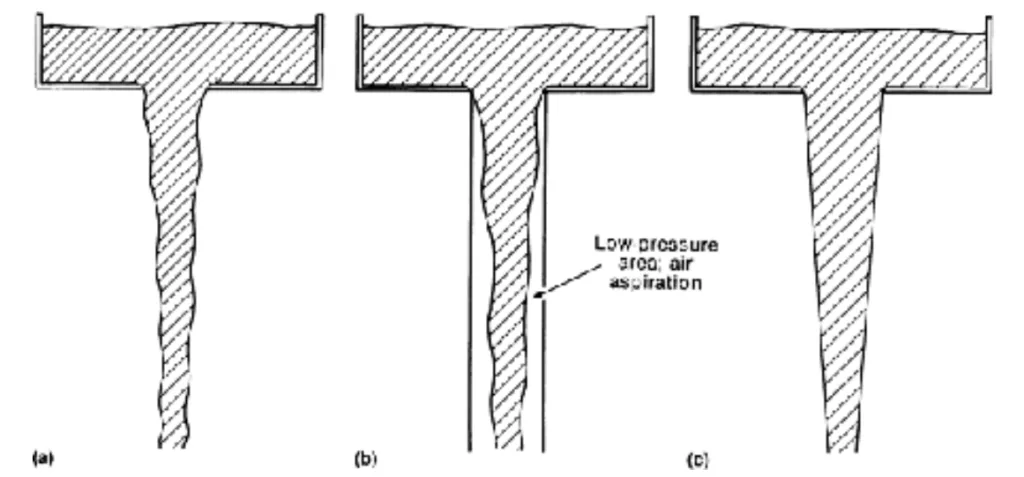
Figure 3: Schematic Showing The Advantages Of A Tapered Sprue Over A Straight-sided Sprue. (a) Natural Flow Of A Free-falling Liquid. (b) Air Aspiration Induced By Liquid Flow In A Straight-sided Sprue. (c) Liquid Flow In A Tapered Sprue (Sylvia J G, 1972)

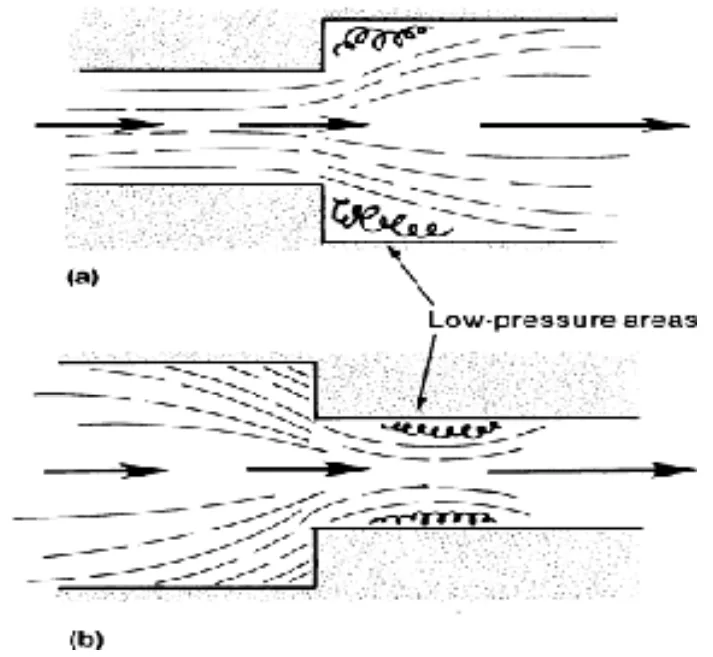
Figure 5: Schematic Showing The Formation Of Low-pressure Areas Due To Abrupt Changes In The Cross Section Of A Flow Channels (a) Sudden Enlargement of the Channel (b) Sudden Reduction of the Channel

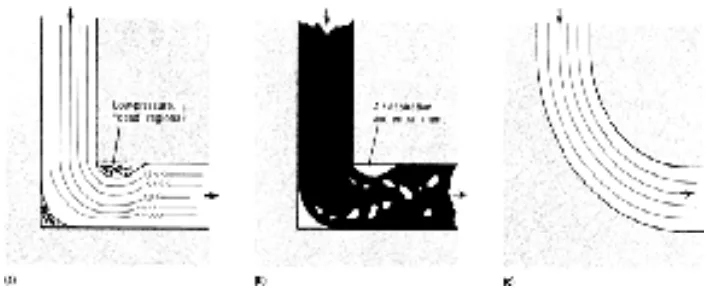
Figure 6: Schematic Illustrating Fluid
Flow Around Right-angle And Curved
Bends In A Gating System (a) Turbulence
Resulting From A Sharp Corner (b) Metal
Damage Resulting From A Sharp Corner
(c) Streamlined Corner That Minimizes
Turbulence And Metal Damage — Figure 6: Schematic Illustrating Fluid Flow Around Right-angle And Curved Bends In A Gating System (a) Turbulence Resulting From A Sharp Corner (b) Metal Damage Resulting From A Sharp Corner (c) Streamlined Corner That Minimizes Turbulence And Metal Damage

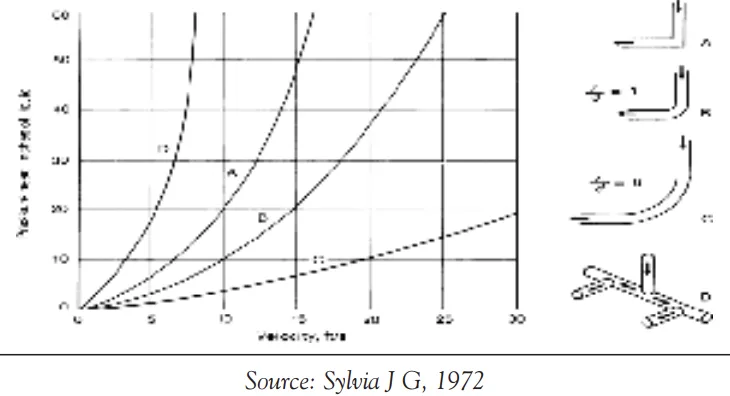
Figure 7: Effect of Pressure Head and Change in Gate Design on the Velocity of Metal Flow: (a) 90° Bend; (b) r/d = 1; (c) r/d = 6; (d) Multiple 90° Bends. The Variables r and d are the Radius of Curvature and the Diameter of the Runner, Respectively

Figure Name List:

Figure 1: Elements of Gating System (Sylvia J G, 1972)
Figure 2: Illustration of Bernoulli's Theorem (Sylvia J G, 1972)
Figure 3: Schematic Showing The Advantages Of A Tapered Sprue Over A Straight-sided Sprue. (a) Natural Flow Of A Free-falling Liquid. (b) Air Aspiration Induced By Liquid Flow In A Straight-sided Sprue. (c) Liquid Flow In A Tapered Sprue (Sylvia J G, 1972)
Figure 4: Choke Mechanisms Incorporated Into Straight-sided Sprues To Approximate Liquid Flow in Tapered Sprues (a) Choke Core (b) Runner Choke (Sylvia J G, 1972)
Figure 5: Schematic Showing The Formation Of Low-pressure Areas Due To Abrupt Changes In The Cross Section Of A Flow Channels (a) Sudden Enlargement of the Channel (b) Sudden Reduction of the Channel
Figure 6: Schematic Illustrating Fluid Flow Around Right-angle And Curved Bends In A Gating System (a) Turbulence Resulting From A Sharp Corner (b) Metal Damage Resulting From A Sharp Corner (c) Streamlined Corner That Minimizes Turbulence And Metal Damage
Figure 7: Effect of Pressure Head and Change in Gate Design on the Velocity of Metal Flow: (a) 90° Bend; (b) r/d = 1; (c) r/d = 6; (d) Multiple 90° Bends. The Variables r and d are the Radius of Curvature and the Diameter of the Runner, Respectively
Figure 8: Applying Bernoulli's Theorem to Flow From a Runner at two Ingates For a Filled System and Comparingvelocity and Pressure at the Ingates for two Runner Configurations (a) Same Runner Cross Section at Bothingates (b) Stepped Runner Providing Two Different Runner Cross Sections at Each Ingate
Figure 9: Heuristics for Ingate Location
Figure 10: Flow Chart of Gating Element Design

7. Conclusion:

Summary of Key Findings:

Pouring basin, sprue, sprue base well, runner and runner extension serves the purpose of allowing clean molten metal to enter the mould cavity.
Parting gate is the most widely used gate.
Fluid mechanics laws and empirical relations are applied to design the optimum gating system.
Important to ensure slag removal before the metal enters the mould cavity.
Sometimes chills may be needed to address porosity.

Academic Significance of the Study:

Provides a comprehensive review of gating system design principles, consolidating knowledge from various sources.

Practical Implications:

Offers practical guidance for designing gating systems to improve casting quality and yield.

Limitations of the Study and Areas for Future Research:

The study primarily relies on existing literature and does not present new experimental data. Future research could focus on validating the presented principles through experimental studies or computational modeling.

8. References:

Atlas of Casting Defects, Institute of British Foundry men.
Guleyupoglu S (1995), “A general approach to the parting direction problem for sand castings”, Ph.D. Thesis, The University of Alabama, Tuscaloosa, AL.
Guleyupoglu S and Hill J L (1995), "Parting direction and parting plane selection criteria forsand castings”, AFS Transactions, Vol. 103, pp. 259-264.
Guleyupoglu S, Yu KO and Hill JL (1996), "Analysis and optimal design of risers based on section modulus method", In Proc. 9th World Conference on Investment Castings, San Francisco, CA, October.
Karsay S I (1981), Ductile Iron III: Gating and Risering, QIT—Fer et Titane, Inc.
Khanna O P (2011), Foundry Technology, 15th Reprint. Principles of Gating, pp. 203-237.
Rao P N (2007), “Manufacturing Technology", Vol. 1, Gating System for Casting, pp. 126-133.
Richins D S and Wetmore W O (1951), AFS Symposium on Principles of Gating, p. 1, AFS, Des Plaines, IL.
Ruddle R W (1956), The Running and Gating of Sand Castings. The Institute of Metals, London, England.
Ruddle R W (1978), “Risering—past, present and future”, British Foundryman, Vol. 71(a), p. 197.
Ruddle R W (1982), “A computer program for steel risering”, AFS Transactions, Vol. 90, pp. 227-237.
Swift R E, Jackson J H and Eastwood L W (1949), “A study of principles of gating”, AFS Transactions, Vol. 57, pp. 76-88.
Sylvia J G (1972), Cast Metals Technology, Addison-Wesley.
Wallace J F and Evans E B (1959), "Principles of Gating”, Foundry, Vol. 87, Oct ober.
WWW.emt-india.net

9. Copyright:

This material is "Mazhar Iqbal"'s paper: Based on "GATING DESIGN CRITERIA FOR SOUND CASTING".
Paper Source: www.ijmerr.com (From the paper's header, Vol. 2, No. 3, July 2014)

PDF View

Tags: Applications; ,CAD; ,Review; ,Sand casting; ,STEP