Multi-component topology optimization for die casting (MTO-D)

This page summarizes the research paper "Multi-component topology optimization for die casting (MTO-D)" published in Structural and Multidisciplinary Optimization in 2019. This summary is intended for informational purposes and to facilitate understanding of the paper's content.

1. Overview:

• Title: Multi-component topology optimization for die casting (MTO-D)
• Author: Hao Zhou, Junyuan Zhang, Yuqing Zhou, Kazuhiro Saitou
• Publication Year: 2019
• Publishing Journal/Academic Society: Structural and Multidisciplinary Optimization
• Keywords: Multi-component topology optimization, Manufacturability, Die cast components, Parting lines

2. Research Background:

• Social/Academic Context of the Research Topic:
  Topology optimization has become an effective tool for structural design and is widely used in industrial applications. However, its primary application remains in designing single-component structures. Most engineered products are assemblies of multiple components. Complex geometries resulting from topology optimization are often uneconomical or impossible to manufacture as single pieces. Partitioning complex geometries into simpler components is crucial, requiring a balance between structural performance and manufacturing costs.
• Limitations of Existing Research:
  Conventional topology optimization largely overlooks geometric constraints imposed by manufacturing processes. This often leads to optimized designs with features that are difficult or impossible to manufacture using available methods. While some post-optimization editing can improve manufacturability, it often results in sub-optimal structural performance. Existing methods for multi-component topology optimization are either computationally inefficient, rely on non-gradient optimization, or have limited applicability to structural assemblies made of multiple components.
• Necessity of the Research:
  There is a clear need for a manufacturability-driven approach to synthesize multi-component structures. Specifically, for die casting processes, it is essential to develop topology optimization methods that inherently consider manufacturing constraints to ensure moldability and reduce manufacturing costs. This research addresses the gap by proposing a multi-component topology optimization method tailored for die casting.

3. Research Purpose and Research Questions:

• Research Purpose:
  The primary purpose of this research is to present a "multi-component topology optimization method for the structural assemblies that are made of components produced by die casting (MTO-D) processes, where each part is guaranteed to be free from fully enclosed cavities and undercuts in the direction of mold drawing."
• Key Research Questions:
  • How can manufacturing constraints specific to die casting processes be effectively integrated into multi-component topology optimization?
  • How can design variables be introduced to specify and optimize the location and orientation of parting lines for each component in a die casting assembly?
  • How can moldability, specifically the absence of undercuts and fully enclosed cavities in the mold drawing direction, be ensured for each component designed using topology optimization?
• Research Hypotheses:
  The proposed MTO-D method, by incorporating new design variables for parting lines and integrating moldability constraints based on the vector method and numerically approximated density gradient, will successfully generate optimized multi-component designs for die casting. These designs will be moldable, free from undercuts and fully enclosed cavities, and achieve minimized compliance.

4. Research Methodology

• Research Design:
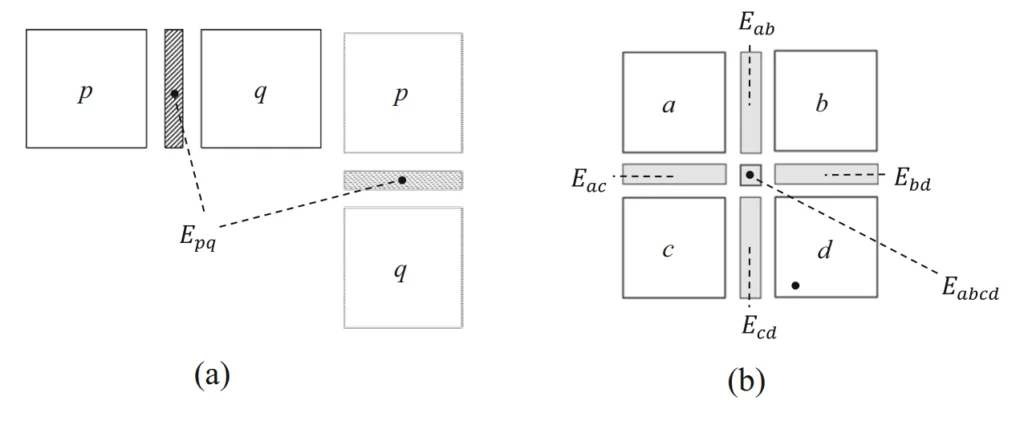
  The research builds upon the authors' previous work on multi-component topology optimization for stamped sheet metal assemblies (MTO-S). The proposed mathematical formulation for MTO-D incorporates new design variables that explicitly define the parting line for each component. Structural elements are clustered into core and cavity halves using the parting line as a linear classifier.
• Data Collection Method:
  The validity and applicability of the proposed MTO-D method are demonstrated through several numerical examples focused on compliance minimization. These examples include benchmark problems such as cantilever beams, bridge structures, and MBB beams under various loading and boundary conditions.
• Analysis Method:
  The presence of undercut features and fully enclosed cavities is evaluated for each mold half using the "vector method with the numerically approximated density gradient." This method assesses the dot product between the draw direction and the density gradient to identify potential moldability issues. A sigmoid function is used to relax conditional changes in draw direction for numerical stability.
• Research Subjects and Scope:
  The research focuses on structural assemblies made of components produced by die casting processes. The scope is limited to 2D examples for demonstrating the methodology. The objective function for optimization is compliance minimization, aiming to achieve structurally efficient designs while ensuring manufacturability.

5. Main Research Results:

• Key Research Results:
  "The optimized results show that each part is indeed moldable with no undercut in the drawing direction and has no fully enclosed cavity." Numerical examples presented in the paper demonstrate the effectiveness of the proposed MTO-D method in generating manufacturable multi-component designs for die casting.
• Statistical/Qualitative Analysis Results:
  The paper primarily presents visual and qualitative results. Optimized structures are shown for various test cases (MBB beam, cantilever beam, bridge structure) and different parameter settings (MABB area limit, number of components, initial parting line directions, grid sizes).
  • Figure 11 shows optimized results for different boundary conditions, demonstrating moldability and absence of undercuts in the drawing direction.
  • Figure 12 compares results with different grid sizes (20×10 and 40×20) for a cantilever beam, showing similar overall geometry and component partitioning, indicating "good mesh-independence property."
  • Figure 13 compares MTO-D results with MTO-S results, highlighting "clear improvements in their moldability over the ones by multi-component topology optimization for sheet stamping (MTO-S)."
  • Figure 14 shows the iteration history curve for the MBB beam example, illustrating the convergence of compliance and MABB area constraint.
  • Figure 16 and Figure 17 present topology optimization results with varying MABB limit values and number of components, respectively, showing the trade-off between structural compliance and volume fraction.
• Data Interpretation:
  The numerical results and visual inspections of the optimized designs confirm that the MTO-D method successfully incorporates die casting manufacturing constraints into the topology optimization process. The method effectively generates multi-component assemblies where each component is moldable, free from undercuts and enclosed cavities, and structurally optimized for compliance. The results also demonstrate the influence of parameters like MABB area limit and number of components on the design outcome, allowing for trade-offs between performance and manufacturing cost.
• Figure Name List:
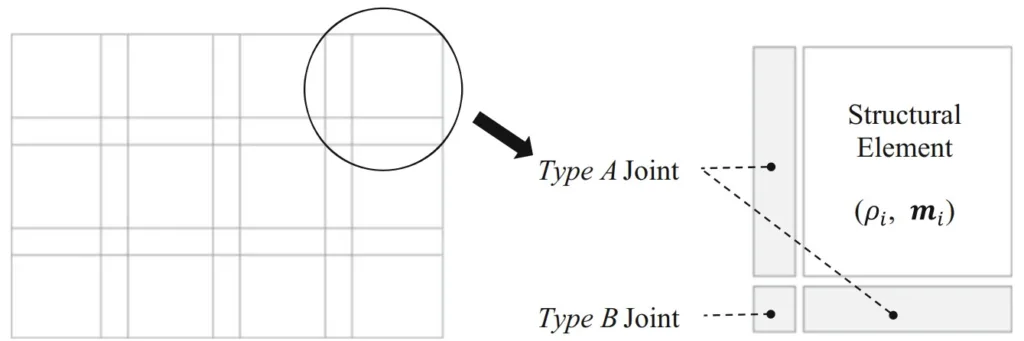
  1. Fig. 1 Domain discretization and two different joint elements
  2. Fig. 2 Stiffness models of joint elements. a Type A joint element and b Type B joint element
  3. Fig. 3 Geometry requirements for cast components: a internal cavity, b undercut, c modified parting line without undercut
  4. Fig. 4 Cartesian representation of orientation in 2D
  5. Fig. 5 Representations of parting line and the drawing direction
  6. Fig. 6 Sigmoid function SL(x) for parting line
  7. Fig. 7 detection of undercuts and internal cavities
  8. Fig. 8 Sigmoid function Su(x) for undercut features
  9. Fig. 9 Approximation of density gradient: a eight finite elements surrounding element i, and b four unit vectors for gradient approximation
  10. Fig. 10 Design domain and boundary condition for three test problem. a Cantilever (2-by-1); b Bridge (4-by-1); c MBB (4-by-1)
  11. Fig. 11 Optimized results for different boundary conditions.
  12. Fig. 12 Comparison between the results (post-processed) with different grid sizes (left: 20×10, right: 40×20) in cantilever beam loading case: (a) Lower case; (b) Upper case
  13. Fig. 13 Comparison between the results (post-processed) by MTO-D (left) and MTO-S (right): a bridge and b cantilever beam (upper loading)
  14. Fig. 14 Iteration history curve for MBB beam example: a objective function and MABB area constraint and b moldability constraint
  15. Fig. 15 Comparison between the results (post-processed) with different initial parting line direction for MBB beam example. For each direction (45/-45/30/60), the assembly and structure for each component are plotted. The red and blue lines are plotted as drawing direction, the green line are parting line
  16. Fig. 16 Topology optimization results with different MABB limit value (red and blue lines: drawing direction, green line: parting line)
  17. Fig. 17 Topology optimization results with different number of components (red and blue lines: drawing direction, green line: parting line): a cantilever beam (upper loading) and b MBB beam

6. Conclusion and Discussion:

• Summary of Main Results:
  This paper successfully presented a novel multi-component topology optimization method for die casting (MTO-D). The method incorporates design variables for parting lines and moldability constraints based on the vector method and sigmoid functions. Numerical examples demonstrated the method's ability to generate moldable multi-component designs free from undercuts and enclosed cavities, while minimizing structural compliance.
• Academic Significance of the Research:
  This research makes significant academic contributions by:
  • Extending topology optimization to address the design of multi-component assemblies with inherent manufacturing considerations.
  • Introducing the parting line as a design variable within the topology optimization framework, enabling simultaneous optimization of topology and component partitioning.
  • Developing and integrating moldability constraints specifically tailored for die casting processes, ensuring manufacturable designs directly from optimization.
• Practical Implications:
  The MTO-D method has significant practical implications for the die casting industry:
  • It enables automated design of die cast components and assemblies, reducing reliance on manual design iterations and expert knowledge.
  • It facilitates the creation of innovative and structurally optimized die cast products with improved performance and reduced material usage.
  • By considering manufacturing costs through MABB area constraints, the method helps in achieving a balance between structural performance and economic viability.
• Limitations of the Research:
  The research acknowledges several limitations:
  • The numerical examples are limited to 2D problems, and further research is needed for 3D implementation.
  • The moldability constraints, while effective, are based on approximations and may not capture all complexities of die casting mold design.
  • The manufacturing cost model is simplified and serves as a surrogate for the actual die set material cost.
  • Despite efforts to eliminate undercuts, some minor undercut features may still appear in optimized designs, indicating room for further refinement of the moldability constraints.

7. Future Follow-up Research:

• Directions for Follow-up Research:
  The authors propose several directions for future research to extend and improve the MTO-D method:
  • 3D Implementation: Developing and validating a 3D implementation of the MTO-D method to address more complex and realistic industrial applications.
  • Improved Density Gradient Calculation: Exploring more general and accurate methods for density gradient calculation, potentially using nodal design variables to handle irregularly shaped design domains.
  • Advanced Cost Models: Incorporating more sophisticated cost models that account for additional mold mechanisms like side pins and core lifters, and die set machining costs.
  • Relaxation of Parting Line Constraints: Relaxing the assumption of straight parting lines to allow for more complex and potentially optimized parting surface geometries.
  • Joint Stress and Interfacial Strength: Including constraints on maximum stress in joints and considering the influence of interfacial strength between different components.
  • Welding Cost Model: Developing and integrating a cost model for welding or other joining processes for die cast components.
• Areas Requiring Further Exploration:
  Further exploration is needed in areas such as:
  • Enhancing the robustness and numerical efficiency of the 3D implementation of MTO-D.
  • Refining the moldability and manufacturing cost models to better represent real-world die casting scenarios.
  • Developing strategies to completely eliminate remaining undercut features in optimized designs and further improve moldability.

8. References:

• Altair Engineering, Inc (2017) Altair HyperWorks 2017.1 user's manual, www.altairhyperworks.com/product/OptiStruct
• Bendsøe MP, Kikuchi N (1988) Generating optimal topologies in structural design using a homogenization method. Comput Methods Appl Mech Eng 71(2):197-224
• Boothroyd G, Dewhurst P, Knight WA (2010) Product design for manufacture and assembly. CRC Press, Boca Raton
• Bruyneel M, Fleury C (2002) Composite structures optimization using sequential convex programming. Adv Eng Softw 33(7-10):697-711
• Chen J, Shapiro V, Suresh K, Tsukanov I (2007) Shape optimization with topological changes and parametric control. Int J Numer Methods Eng 71(3):313-346
• Chickermane H, Gea HC (1997) Design of multi-component structural systems for optimal layout topology and joint locations. Eng Comput 13(4):235-243
• Fu MW, Nee AY, Fuh JY (2002) The application of surface visibility and moldability to parting line generation. Comput Aided Des 34(6): 469-480
• Gaynor AT, Guest JK (2016) Topology optimization considering overhang constraints: eliminating sacrificial support material in additive manufacturing through design. Struct Multidiscip Optim 54(5): 1157-1172
• Gersborg AR, Andreasen CS (2011) An explicit parameterization for casting constraints in gradient driven topology optimization. Struct Multidiscip Optim 44(6):875-881
• Guest JK, Asadpoure A, Ha SH (2011) Eliminating beta-continuation from Heaviside projection and density filter algorithms. Struct Multidiscip Optim 44(4):443-453
• Guirguis D, Hamza K, Aly M, Hegazi H, Saitou K (2015) Multi-objective topology optimization of multi-component continuum structures via a Kriging-interpolated level set approach. Struct Multidiscip Optim 51(3):733-748
• Guo X, Zhou J, Zhang W, Du Z, Liu C, Liu Y (2017) Self-supporting structure design in additive manufacturing through explicit topology optimization. Comput Methods Appl Mech Eng 323:27-63
• Harzheim L, Graf G (2006) A review of optimization of cast parts using topology optimization. Struct Multidiscip Optim 31(5):388-399
• Hicks J (1999) Welded joint design, 3rd edn. Industrial Press, New York
• Hughes TJ (2000) The finite element method: linear static and dynamic finite element analysis. Dover Publications, MI
• Jiang T, Chirehdast M (1997) A systems approach to structural topology optimization: designing optimal connections. J Mech Des 119(1): 40-47
• Johanson R, Kikuchi N, Papalambros P (1994) Simultaneous topology and material microstructure design. Adv Struct Optim:143-149
• Kang Z, Wang Y, Wang Y (2016) Structural topology optimization with minimum distance control of multiphase embedded components by level set method. Comput Methods Appl Mech Eng 306:299-318
• Langelaar M (2017) An additive manufacturing filter for topology optimization of print-ready designs. Struct Multidiscip Optim 55(3): 871-883
• Li Q, Chen W, Liu S, Fan H (2018) Topology optimization design of cast parts based on virtual temperature method. Comput Aided Des 94: 28-40
• Li Q, Steven GP, Xie YM (2001a) Evolutionary structural optimization for connection topology design of multi-component systems. Eng Comput 18(3/4):460-479
• Li Y, Xin X, Kikuchi N, Saitou K (2001b) Optimal shape and location of piezoelectric materials for topology optimization of flextensional actuators. In Proceedings of the 3rd annual conference on genetic and evolutionary computation (pp. 1085-1090). Morgan Kaufmann Publishers Inc.
• Lim JY, Yoon MJ, Kim SY, Shin HS, Kim TG (2015) Mechanical properties of CO2/MIG welded structural rolled steel and stainless steel. J Mech Sci Technol 29(1):103-108
• Liu J, Gaynor AT, Chen S, Kang Z, Suresh K, Takezawa A, Cheng L. (2018) Current and future trends in topology optimization for additive manufacturing. Struct Multidiscip Optim 57(6):2457-2483.
• Liu P, Kang Z (2018) Integrated topology optimization of multi-component structures considering connecting interface behavior. Comput Methods Appl Mech Eng 341:851-887
• Liu S, Li Q, Chen W, Tong L, Cheng G (2015) An identification method for enclosed voids restriction in manufacturability design for additive manufacturing structures. Front Mech Eng 10(2):126-137
• Lyu N, Saitou K (2005) Topology optimization of multicomponent beam structure via decomposition-based assembly synthesis. J Mech Des 127(2):170-183
• MathWorks, Inc (2016) MATLAB Primer, R2016a edition. www. mathworks.com
• Mirzendehdel AM, Suresh K (2016) Support structure constrained topology optimization for additive manufacturing. Comput Aided Des 81:1-13
• Nomura T, Dede EM, Lee J, Yamasaki S, Matsumori T, Kawamoto A, Kikuchi N (2015) General topology optimization method with continuous and discrete orientation design using isoparametric projection. Int J Numer Methods Eng 101(8):571-605
• Qian X (2017) Undercut and overhang angle control in topology optimization: a density gradient based integral approach. Int J Numer Methods Eng 111(3):247-272
• Qian Z, Ananthasuresh GK (2004) Optimal embedding of rigid objects in the topology design of structures. Mech Based Des Struct Mach 32(2):165-193
• Ravi B, Srinivasan MN (1990) Decision criteria for computer-aided parting surface design. Comput Aided Des 22(1):11-18
• Rozvany GI, Zhou M, Birker T (1992) Generalized shape optimization without homogenization. Struct Optim 4(3–4):250-252
• Sato Y, Yamada T, Izui K, Nishiwaki S (2017) Manufacturability evaluation for molded components using fictitious physical models, and its application in topology optimization. Int J Adv Manuf Technol 92(1-4):1391-1409
• Sigmund O (2001) A 99 line topology optimization code written in Matlab. Struct Multidiscip Optim 21(2):120-127
• Stegmann J, Lund E (2005) Discrete material optimization of general composite shell structures. Int J Numer Methods Eng 62(14): 2009-2027
• Vanderplaats Research and Development, Inc (2017) GENESIS 16.0 User's Manual, www.vrand.com/products/genesis/
• Vatanabe SL, Lippi TN, de Lima CR, Paulino GH, Silva EC (2016) Topology optimization with manufacturing constraints: a unified projection-based approach. Adv Eng Softw 100:97-112
• Wang Y, Gao J, Kang Z (2018) Level set-based topology optimization with overhang constraint: towards support-free additive manufacturing. Comput Methods Appl Mech Eng 339:591-614
• Wang Y, Kang Z (2017) Structural shape and topology optimization of cast parts using level set method. Int J Numer Methods Eng 111(13): 1252-1273
• Wang X, Kang Z, Wang Y (2011) Topology design of slender piezoelectric actuators with repetitive component patterns. J Intell Mater Syst Struct 22(18):2161-2172
• Wang MY, Wang X, Guo D (2003) A level set method for structural topology optimization. Comput Methods Appl Mech Eng 192(1- 2):227-246
• Weinstein M, Manoochehri S (1997) Optimum parting line design of molded and cast parts for manufacturability. J Manuf Syst 16(1):1
• Xia Q, Shi T, Wang MY, Liu S (2010) A level set based method for the optimization of cast part. Struct Multidiscip Optim 41(5):735–747
• Yildiz AR, Saitou K (2011) Topology synthesis of multicomponent structural assemblies in continuum domains. J Mech Des 133(1):011008
• Zhang W, Zhou L (2018) Topology optimization of self-supporting structures with polygon features for additive manufacturing. Comput Methods Appl Mech Eng 334:56-78
• Zhou M, Fleury R, Shyy YK, Thomas H, and Brennan J (2002) Progress in topology optimization with manufacturing constraints. In 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization (p. 5614)
• Zhou Y, Saitou K (2017) Topology optimization of composite structures with data-driven resin filling time manufacturing constraint. Struct Multidiscip Optim 55(6):2073-2086
• Zhou Y, Saitou K (2018) Gradient-based multi-component topology optimization for stamped sheet metal assemblies (MTO-S). Struct Multidiscip Optim 58(1):83-94
• Zhou Y, Nomura T, Saitou K (2018) Multi-component topology and material orientation design of composite structures (MTO-C). Comput Methods Appl Mech Eng 342:438-457
• Zhou Y, Nomura T, Saitou K (2019) Multicomponent topology optimization for additive manufacturing with build volume and cavity free constraints. J Comput Inf Sci Eng 19(2):021011
• Zhu JH, Gu XJ, Zhang WH, Beckers P (2013) Structural design of aircraft skin stretch-forming die using topology optimization. J Comput Appl Math 246:278-288
• Zhu J, Zhang W, Beckers P, Chen Y, Guo Z (2008) Simultaneous design of components layout and supporting structures using coupled shape and topology optimization technique. Struct Multidiscip Optim 36(1):29-41
• Zhu JH, Zhang WH, Xia L (2016) Topology optimization in aircraft and aerospace structures design. Archiv Comput Methods Eng 23(4): 595-622

9. Copyright:

• This material is Hao Zhou, Junyuan Zhang, Yuqing Zhou, Kazuhiro Saitou's paper: Based on Multi-component topology optimization for die casting (MTO-D).
• Paper Source: https://doi.org/10.1007/s00158-019-02317-4

This material was summarized based on the above paper, and unauthorized use for commercial purposes is prohibited.
Copyright © 2025 CASTMAN. All rights reserved.