고출력 밀도 애플리케이션을 위한 외부 회전자 유도 전동기의 열 모델 파라미터화

본 소개 논문의 내용은 Przegląd Elektrotechniczny에서 발행한 논문 "Parametrization of the thermal model of induction motor with outer rotor"를 기반으로 합니다.

1. 개요:

• 제목: 외부 회전자 유도 전동기의 열 모델 파라미터화
• 저자: Szczepan Opach, Tomasz Wolnik
• 발행년도: 2023년
• 발행 저널/학회: Przegląd Elektrotechniczny
• 키워드: CFD 시뮬레이션, 열 모델, 유도 전동기, 고출력 밀도 전동기

2. 초록:

본 논문에서는 고출력 밀도의 외부 회전자 유도 전동기를 예로 들어 전동기의 열 모델 파라미터화 방법을 제시한다. 본 논문에서 제시하는 시뮬레이션은 정격 출력 25kW, 질량 16kg의 구리 회전자 케이지를 갖춘 전동기 모델을 사용하여 수행하였다. 이러한 구조는 가해지는 가혹한 작동 조건으로 인해 설계 단계에서 정확한 열 해석이 필요하다. 많은 연구에서 이러한 해석은 일반적으로 전동기의 회전 요소를 고려하지 않은 열 시뮬레이션으로 제한된다. 본 논문에서는 회전자의 회전 운동, 로터 본체의 외부 표면과 환경 간의 대류 열교환 강도를 기술하는 대류 계수, 고정자 권선 열전도율의 대체 수치 결정 방법을 고려하여 에어 갭을 통과하는 열전달 계수 값을 포함하여 CFD 모델의 선택된 파라미터의 수치적 결정 방법을 제시한다. 수치 시뮬레이션에서 얻은 결과를 바탕으로 전동기의 3차원 CFD 모델을 개발하고 해석하였다.

3. 서론:

최근 몇 년간의 방향 중 하나는 희토류 영구 자석에 의존하지 않는 고효율 전기 구동 장치의 개발이다[1-5]. 이는 소위 비출력[kW/kg], 즉 주어진 기계의 출력 밀도를 알려주는 구동 장치에도 적용된다[1,4,6]. 또한, 최근 전기 기계에 대한 소음 감소, 신뢰성, 그리고 궁극적으로 재료 및 생산 비용에 대한 요구 사항 증가는 설계 최적화를 강요하고 있다[7-8]. 물론 기술 및 작동 파라미터 측면에서 영구 자석을 갖춘 모터는 기본적으로 경쟁자가 없으며 최고의 특성을 갖는다. 그러나 주요 부품의 다양화 및 글로벌 독점으로부터의 독립을 포함하여 중요한 문제의 전체 스펙트럼을 고려할 때 유도 전동기를 포함한 다른 유형의 기계 개발 및 개선에 대한 관심이 다시 높아지고 있다. 모터 설계 단계에서 중요한 과제는 모터의 적절한 열 모델 및 열 시뮬레이션[6,9,10]이다. 고출력 밀도 모터는 종종 [12-15 A/mm²]의 고전류 부하 및 고전원 전압 주파수 [800-1000 Hz] 조건에서 작동하므로 이러한 기계의 기계 구조 부품은 부의 열 영향 [11-12]에 특히 노출된다. 여기에는 권선, 베어링, 영구 자석, 샤프트 씰, 엔코더 [9]가 포함된다. 전기 기계의 열 상태의 영향은 부품의 끼워맞춤, 조립 간극 또는 연결 설계를 선택할 때도 고려해야 한다. 전기 기계의 열 상태가 효율에 미치는 영향도 크다[9,13].

현재 많은 과학 연구에서 전기 자동차 분야 (자동차, 항공, 해운) [6,14,15] 용 전기 기계의 열 계산에 주의를 기울이고 있다. 또한 열 계산 문제는 비출력이 높은 모터를 설계할 경우 특히 중요하다. 이러한 계산에서는 CFD 열 유체 시뮬레이션을 사용하여 임의의 작동점 (예: 정격 또는 과부하)에서 부하가 걸린 전기 기계의 정상 상태 열 상태를 결정한다. CFD 계산은 또한 냉각 시스템의 효율을 최적화하여 전기 기계로부터의 열 제거를 강화할 수 있게 한다.

3차원 CDF 모델은 이전에 준비되고 적절하게 단순화된 3차원 CAD 모델과 사용되는 구조 재료의 특성을 기반으로 개발된다. 여기에는 다음이 포함된다.

• 재료의 열전도율 λ (W/mK)
• 재료의 비열 Cp (J/kgK)
• 재료 밀도 ρ (kg/m³)
• 액체의 동점성 η (kg/ms)
• 액체의 동점성 ν (m²/s)

또한 CFD 모델은 작업의 소위 경계 조건을 고려하여 준비된다. 경계 조건에는 다음과 같은 것들이 있다.

• 주변 온도 Ta (°C)
• 단위 시간당 냉각수 유량 F (kg/s)
• 냉각 시스템 입구에서의 온도 Tin (°C) 또는 유체 압력 Pin (bar)
• 자연 대류 계수 an (W/m²K) 및 강제 대류 계수 af (W/m²K)
• 모델의 열 장벽을 통과하는 열전달 계수 k (W/m²K) 또는 이들의 역수인 열 장벽의 열 저항 Rt (m²K/W)

모델의 열 부하, 즉 전력 손실 ΔP (W) 값은 단위 시간당 전기 기계의 개별 부품에서 생성되는 열에너지의 양을 나타낸다. 가장 일반적인 값은 다음의 전력 손실이다.

• 고정자 권선 ΔPcus (W)
• 고정자 코어 ΔPFes (W)
• 회전자 권선 ΔPcur (W)
• 회전자 코어 ΔPFer (W)
• 베어링의 기계적 손실 ΔPb

4. 연구 요약:

연구 주제 배경:

고출력 밀도 전동기, 특히 유도 전동기는 특히 전기 모빌리티에서 점점 더 중요해지고 있다. 이러한 모터는 신뢰성과 효율성을 보장하기 위해 정확한 열 관리가 필요한 까다로운 조건에서 작동한다. 정확한 열 해석은 설계 단계에서 필수적이다.

선행 연구 현황:

기존의 열 해석에서는 회전 부품을 무시하고 대류 계수에 일정한 값을 사용하여 모델을 단순화하는 경우가 많았다. CFD 모델에서 에어 갭의 메시 분할도 모터 전체 치수에 비해 치수가 작기 때문에 메시 품질 문제 (종횡비)를 일으켜 과제가 되고 있다.

연구 목적:

본 연구는 고출력 밀도 외부 회전자 유도 전동기의 파라미터화된 열 모델을 개발하는 것을 목표로 하며, CFD 모델링을 위한 주요 파라미터의 수치적 결정에 초점을 맞추고 있다. 여기에는 다음이 포함된다.

• 회전자의 움직임을 고려한 에어 갭을 통과하는 열전달 계수 kag (W/m²K).
• 외부 회전자 표면의 대류 계수 af (W/m²K).
• 고정자 권선의 대체 열전도율 계수 Axy, Az (W/mK).

핵심 연구:

본 연구는 8000rpm으로 작동하는 25kW, 16kg 구리 케이지 외부 회전자 유도 전동기의 3D CFD 열 모델의 파라미터를 수치적으로 결정하는 데 초점을 맞추고 있다. 목표는 모터 부품의 정상 상태 온도를 정확하게 예측하고 냉각수의 열 제거 효율을 분석하는 것이다.

5. 연구 방법

연구 설계:

본 연구에서는 전산 유체 역학 (CFD) 소프트웨어 ANSYS 2021 R2 Fluent를 사용한 수치 시뮬레이션을 채택하였다. 열 모델의 파라미터화는 중요한 열전달 파라미터를 결정하기 위한 일련의 전용 수치 실험을 통해 달성되었다.

데이터 수집 및 분석 방법:

• 에어 갭을 통과하는 열전달 계수 (kag): 3D 에어 갭 모델을 만들고 ANSYS Fluent에서 시뮬레이션을 수행하여 회전자 회전을 고려하여 에어 갭의 등가 열 저항 Rtag (m²K/W)를 수치적으로 결정하였다. 온도 T1과 T2를 원통형 표면에 할당하고 열 유속 q (W)를 계산하여 식 (2)를 사용하여 kag와 Rtag를 유도하였다.
• 외부 회전자 표면의 강제 대류 계수 (af): 회전자와 주변 공기의 2D 모델을 시뮬레이션하였다. 다양한 온도차 ΔT와 회전 속도에 대한 수치 시뮬레이션을 수행하여 단위 열 유속 ġ (W/m²)를 결정하고, 이어서 식 (3)을 사용하여 af를 계산하였다.
• 슬롯 단면에서 고정자 권선의 등가 열전도율 계수 (Axy): "정사각형" 및 "삼각형" 구성으로 배열된 권선 와이어가 있는 고정자 슬롯의 2D 모델을 시뮬레이션하였다. 주어진 온도차 ΔT에 대한 열 유속 q (W)를 계산하여 식 (1)을 사용하여 대체 열전도율 계수 Axy를 결정하였다.

연구 주제 및 범위:

본 연구는 고출력 밀도 애플리케이션용으로 설계된 구리 케이지 외부 회전자 유도 전동기에 초점을 맞추고 있다. 범위는 다음을 포함한다.

• 회전자 회전을 고려한 에어 갭 열전달 계수의 수치적 결정.
• 외부 회전자 표면의 강제 대류 계수의 수치적 결정.
• 고정자 권선의 등가 열전도율의 수치적 결정.
• 모터의 3D CFD 열 모델 개발 및 해석.
• 정상 상태 온도 분포 및 냉각수 열 제거 분석.

6. 주요 결과:

주요 결과:

• 에어 갭을 통과하는 열전달 계수 kag는 회전자 운동을 고려하여 수치적으로 결정되었으며, 에어 갭의 등가 열 저항은 Rtag = 0.00773 m²K/W인 것으로 밝혀졌다.
• 외부 회전자 본체의 외부 표면의 강제 대류 계수 af는 회전 속도 8000 rpm에서 58.43 W/m²K, 4000 rpm에서 32.76 W/m²K로 수치적으로 결정되었다.
• 슬롯 단면에서 고정자 권선의 등가 열전도율 계수 Axy는 "정사각형" 구성에서 함침 바니시 충전 시 1.39 W/mK로 결정되었다.
• 이러한 수치적으로 유도된 계수 및 열 저항 (표 11)으로 파라미터화된 3D CFD 모델을 해석하여 모터의 정상 상태 열 거동을 예측하였다 (그림 11-17).
• 냉각수 (물)의 온도 상승은 ΔT = 3.1 °C로 계산되었으며, 이는 냉각 시스템에 의한 효율적인 열 제거를 나타낸다.

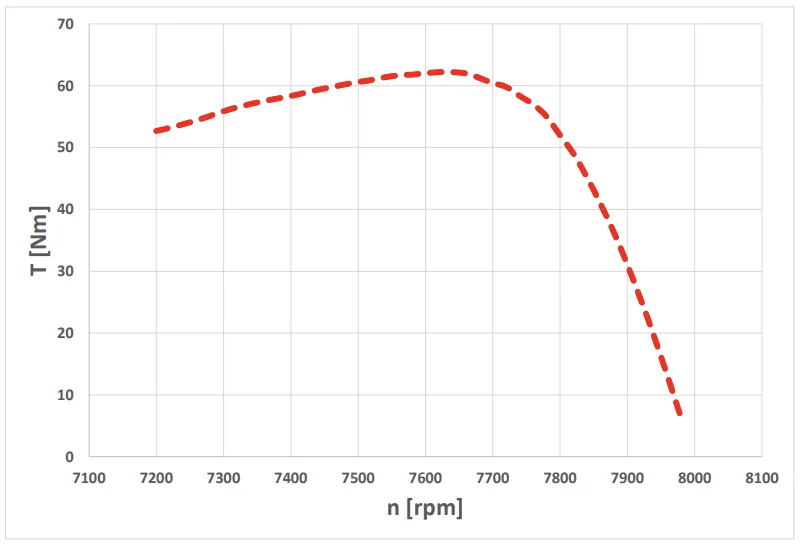
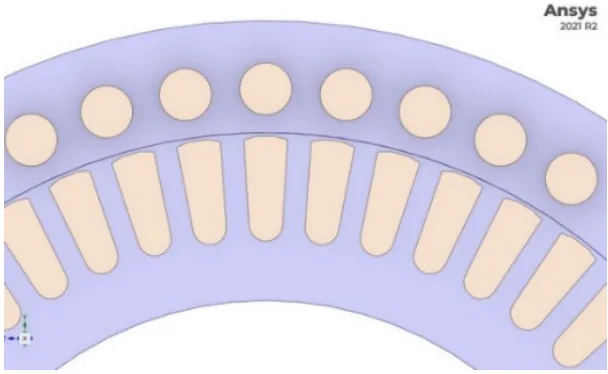
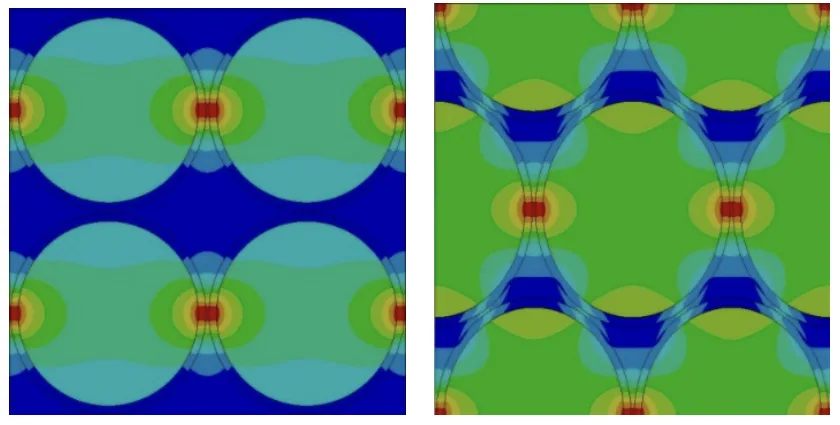
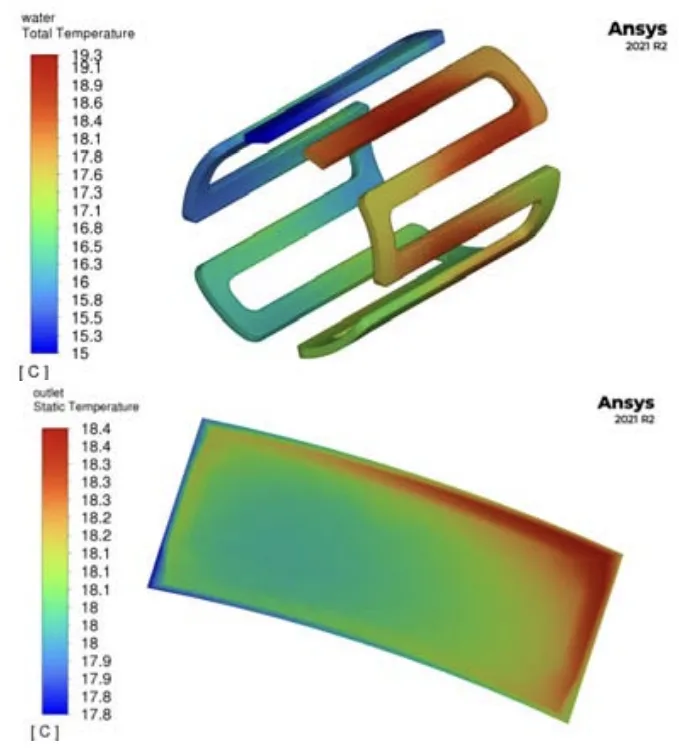
그림 목록:

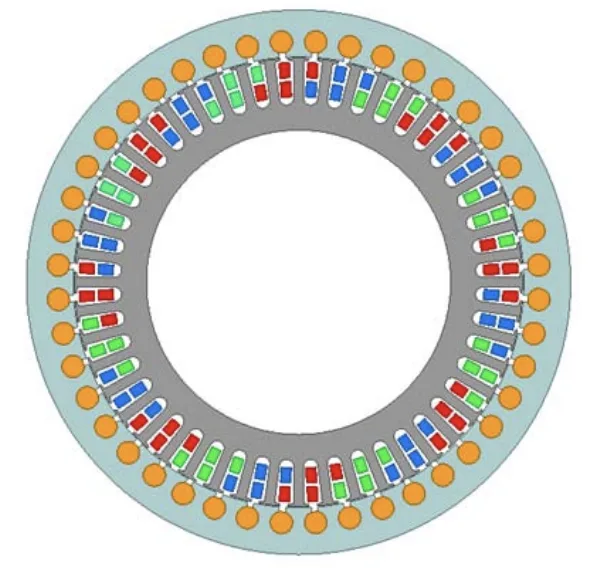
• Fig. 1. 외부 회전자 유도 전동기의 전자기 회로 모델.
• Fig. 2. 회전 속도 특성에 대한 토크.
• Fig. 3. 외부 회전자 유도 전동기의 CAD 모델
• Fig. 4. ANSYS 소프트웨어에서 유한 요소 메시가 있는 모터 모델
• Fig. 5. ANSYS 소프트웨어에서 유한 요소 메시가 있는 냉각수
• Fig. 6. 에어 갭을 생략한 유도 전동기의 고정자 및 회전자 단순화 모델
• Fig. 7. ANSYS에서 유한 요소 메시가 있는 에어 갭의 3D 모델
• Fig. 8. 회전 속도 n = 8000 rpm에서 회전자 주변의 온도 분포.
• Fig. 9. 슬롯을 채운 "정사각형" 및 "삼각형" 구성의 테스트 샘플의 온도 분포 (함침 바니시 채움).
• Fig. 10. 슬롯을 채운 "정사각형" 및 "삼각형" 구성의 테스트 샘플의 온도 분포 (공기 채움).
• Fig. 11. 권선 및 고정자 코어에서 계산된 열 정상 상태
• Fig. 12. 구리 케이지 회전자에서 계산된 열 정상 상태
• Fig. 13. 회전자 코어에서 계산된 열 정상 상태
• Fig. 14. 회전자 하우징에서 계산된 열 정상 상태
• Fig. 15. 고정자 하우징에서 계산된 열 정상 상태
• Fig. 16. 샤프트 및 베어링에서 계산된 열 정상 상태
• Fig. 17. 냉각수 (물)의 계산된 열 정상 상태

7. 결론:

본 연구에서는 고출력 밀도의 외부 회전자 유도 전동기의 열 모델을 파라미터화하는 방법을 성공적으로 제시하였다. 수치적 방법을 사용하여 에어 갭을 통과하는 열전달 계수, 외부 회전자 표면의 대류 계수, 고정자 권선의 등가 열전도율과 같은 중요한 파라미터를 결정하였다. 이러한 파라미터를 그 후 3D CFD 모델의 개발 및 해석에 활용하여 모터의 열 거동을 정확하게 예측할 수 있게 되었다. 결과는 고출력 밀도 모터의 상세한 열 해석을 위한 제안된 방법의 유효성을 입증하며, 최적화된 설계 및 효율적인 냉각 시스템으로 이어진다.

8. 참고 문헌:

• [1] A. Chiba, K. Kiyota, N. Hoshi, M. Takemoto, and S. Ogasawara, 'Development of a Rare-Earth-Free SR Motor With High Torque Density for Hybrid Vehicles', IEEE Trans. Energy Convers., vol. 30, no. 1, pp. 175-182, Mar. 2015, doi: 10.1109/TEC.2014.2343962.
• [2] M. Morimoto, 'Iron loss of non-rare earth traction motor for electric vehicle', in 2010 IEEE Vehicle Power and Propulsion Conference, Lille, France: IEEE, Sep. 2010, pp. 1-4. doi: 10.1109/VPPC.2010.5729030.
• [3] N. G. Ozcelik, U. E. Dogru, M. Imeryuz, and L. T. Ergene, 'Synchronous Reluctance Motor vs. Induction Motor at Low-Power Industrial Applications: Design and Comparison', Energies, vol. 12, no. 11, p. 2190, Jun. 2019, doi: 10.3390/en12112190.
• [4] J. D. Widmer, R. Martin, and M. Kimiabeigi, 'Electric vehicle traction motors without rare earth magnets', Sustainable Materials and Technologies, vol. 3, pp. 7-13, Apr. 2015, doi: 10.1016/j.susmat.2015.02.001.
• [5] T. Wolnik, P. Dukalski, B. Będkowski, T. Jarek 'Selected aspects of designing motor for direct vehicle wheel drive', Przeglad Elektrotechniczny, vol. 1, no. 4, pp. 152-155, Apr. 2020, doi: 10.15199/48.2020.04.31.
• [6] Y. Xia, Y. Han, Y. Xu, and M. Ai, 'Analyzing Temperature Rise and Fluid Flow of High-Power-Density and High-Voltage Induction Motor in the Starting Process', IEEE Access, vol. 7, pp. 35588-35595, 2019, doi: 10.1109/ACCESS.2019.2899346.
• [7] P. Dukalski and R. Krok, 'Selected Aspects of Decreasing Weight of Motor Dedicated to Wheel Hub Assembly by Increasing Number of Magnetic Poles', Energies, vol. 14, no. 4, p. 917, Feb. 2021, doi: 10.3390/en14040917.
• [8] T. Wolnik, V. Styskala, and T. Micak, 'Study on the Selection of the Number of Magnetic Poles and the Slot-Pole Combinations in Fractional Slot PMSM Motor with a High Power Density', Energies, vol. 15, no. 1, p. 215, Dec. 2021, doi: 10.3390/en15010215.
• [9] J. Madej and B. Będkowski, 'Air flow analysis for electrical motor's cooling system with autodesk simulation CDF 2013 program', Acta Mechanica et Automatica, vol. 7, no. 2, pp. 89-92, Jun. 2013, doi: 10.2478/ama-2013-0016.
• [10] B. Będkowski and J. Madej, 'The innovative design concept of thermal model for the calculation of the electromagnetic circuit of rotating electrical machines', Eksploatacja i Niezawosność, vol. 17, no. 4, pp. 481-486, Sep. 2015, doi: 10.17531/ein.2015.4.1.
• [11] T. Wolnik, 'LEMOK – silnik o dużej gęstości mocy', Maszyny Elektryczne - Zeszyty Problemowe, no. 1(127), 2022, pp. 107-110.
• [12]T. Wolnik, T. Jarek, J. Golec, R. Topolewski, and D. Jastrzębski, 'High Power Density Motor for Light Electric Aircraft – Design Study and Lab Tests', in 2023 IEEE Workshop on Electrical Machines Design, Control and Diagnosis (WEMDCD), Newcastle upon Tyne, United Kingdom: ΙΕΕΕ, Apr. 2023, pp. 1-6. doi: 10.1109/WEMDCD55819.2023.10110934.
• [13] B. Bedkowski, P. Dukalski, T. Jarek, and T. Wolnik, 'Numerical model for thermal calculation analysis of the wheel hub motor for electric car verified by laboratory tests', IOP Conf. Ser.: Mater. Sci. Eng., vol. 710, no. 1, p. 012018, Dec. 2019, doi: 10.1088/1757-899X/710/1/012018.
• [14]P. Dukalski and B. Będkowski, 'Obliczenia cieplne silnika elektrycznego do zabudowy w piaście koła samochodu' Napędy i Sterowanie, vol. 24, no.7/8, pp. 70-76.
• [15]Ł. Cyganik and B. Będkowski, 'Układ mechaniczny przełączania zazębienia pomiędzy silnikiem elektrycznym, przekładnią planetarną oraz piastę koła w napędzie elektrycznym zabudowanym w kole pojazdu' Maszyny Elektryczne - Zeszyty Problemowe, no. 1(127), 2022, pp. 117-122.
• [16] B. Będkowski, J. Madej, 'Wyznaczenie zastępczej rezystancji cieplnej izolacji żłobkowej badania I symulacje Maszyny Elektryczne - Zeszyty Problemowe, 2(106), 2015, pp. 117-122.
• [17]P. Mynarek, 'Zastosowanie metody homogenizacji do wyznaczania współczynnika przewodnictwa cieplnego w silnikach elektrycznych', Przegląd Elektrotechniczny, vol. 1, no. 1, pp. 183-186, Jan. 2017, doi: 10.15199/48.2017.01.44.
• [18]P. Mynarek and M. Kowol, 'Metoda homogenizacji uzwojeń wsypywanych W maszynach elektrycznych' Maszyny Elektryczne - Zeszyty Problemowe, 1(105), 2015, pp. 149-154.
• [19] G. Kondziołka, 'Kryteria doboru syciw oraz lakierów elektroizolacyjnych' Maszyny Elektryczne - Zeszyty Problemowe, 2(102), 2014, pp. 7-10.
• [20]S. Opach, 'Obliczenia wartości zastępczej rezystancji cieplnej szczeliny powietrznej w wirnikowych maszynach elektrycznych, Maszyny Elektryczne - Zeszyty Problemowe, no. 1(127), 2022, pp. 101-105.
• [21]D. A. Howey, P. R. N. Childs, and A. S. Holmes, 'Air-Gap Convection in Rotating Electrical Machines', IEEE Trans. Ind. Electron., vol. 59, no. 3, pp. 1367-1375, Mar. 2012, doi: 10.1109/ΤΙΕ.2010.2100337.

9. 저작권:

• 본 자료는 "[Szczepan Opach, Tomasz Wolnik]"의 논문입니다. "[Parametrization of the thermal model of induction motor with outer rotor]"을 기반으로 함.
• 논문 출처: doi:10.15199/48.2023.12.45

본 자료는 상기 논문을 기반으로 요약한 것이며, 상업적 목적으로 무단 사용하는 것을 금지합니다.
Copyright © 2025 CASTMAN. All rights reserved.