CFD를 이용한 고압 다이캐스팅 머신의 숏 슬리브 임계 속도 결정에 관하여

이 소개 논문은 "[Preprint submitted to Elsevier]"에 의해 출판된 논문 "[On determining the critical velocity in the high-pressure die casting machine's shot sleeve using CFD]"에 기반합니다.

1. 개요:

• 제목: CFD를 이용한 고압 다이캐스팅 머신의 숏 슬리브 임계 속도 결정에 관하여 (On determining the critical velocity in the high-pressure die casting machine's shot sleeve using CFD)
• 저자: S. Kohlstädt, M. Vynnycky, S. Goeke, A. Gebauer-Teichmann
• 발행 연도: 2019
• 발행 학술지/학회: Preprint submitted to Elsevier
• 키워드: 압축성 2상 유동, 유체-구조 상호작용, 고압 다이캐스팅, 숏 슬리브, 임계 속도 (compressible two-phase flow, fluid-structure interaction, high-pressure die casting, shot sleeve, critical velocity)

2. 초록:

본 논문은 고압 다이캐스팅에서 피스톤 운동의 저속 구간 동안의 임계 플런저 속도와 이를 오픈 소스 소프트웨어의 CFD 방법을 사용하여 어떻게 결정할 수 있는지 조사합니다. 용탕-공기 시스템은 공기를 압축성 이상 기체로 취급하는 오일러리안 유체 체적법(Eulerian volume-of-fluid) 접근 방식을 통해 모델링됩니다. 난류는 Menter SST k-ω 모델을 사용하는 RANS 접근 방식을 통해 처리됩니다. 메쉬 이동에 대한 두 가지 다른 전략이 제시되고 서로 비교됩니다. 솔버는 해석 모델 및 실험 데이터를 통해 검증됩니다. 그런 다음 2D 메쉬를 사용하여 최적 속도를 결정하는 방법이 제시됩니다. 두 번째 단계에서는 이러한 결과가 실제 3D 형상에 대해 얻은 결과 및 다이의 인게이트 시스템 시뮬레이션 결과와 어떻게 일치하는지 논의합니다.

3. 서론:

고압 다이캐스팅(HPDC)은 자동 변속기 하우징 및 기어 박스 부품과 같은 대량 생산 및 저비용 자동차 부품 제조에 중요한 공정입니다 [1-4]. 일반적으로 알루미늄 또는 마그네슘인 액체 금속은 숏 슬리브 챔버에 부어지고 복잡한 게이트 및 러너 시스템을 통해 일반적으로 50~100 ms⁻¹의 고속으로, 최대 100 MPa의 매우 높은 압력 하에서 다이로 사출됩니다. 일반적인 고압 다이캐스팅 공정은 일반적으로 세 단계로 구성됩니다. 이 단계들은 다음 그림에 나와 있습니다 (figure 1은 이 단계들을 보여줍니다. 왼쪽에서 오른쪽으로: 예비 충전, 다이 충전(숏), 가압 유지). 본 논문의 내용은 첫 번째 단계 동안의 공정을 중심으로 전개될 것입니다.

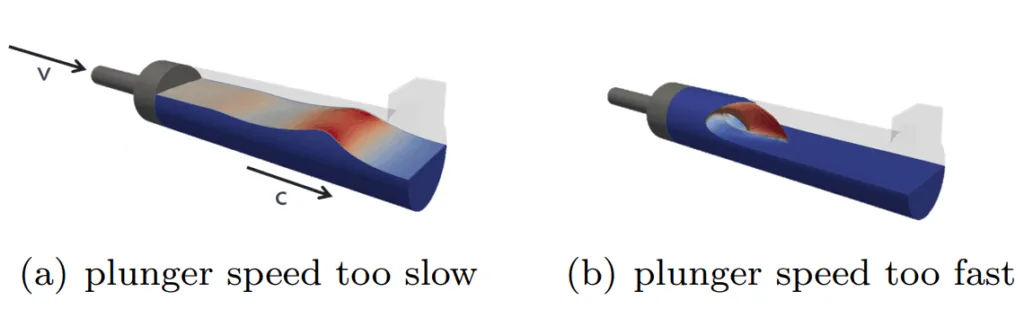
이 공정의 한 가지 측면은 고압 다이캐스팅 머신의 숏 슬리브에서 일어나는 유동 공정입니다. 피스톤 직경, 챔버 내 용탕 높이 및 챔버 길이의 각 조합에 대해 해석적으로 [5, 6] 또는 실험적으로 [7] 결정될 수 있는 정확히 하나의 임계 속도가 있습니다. Faura 등은 또한 해당 속도에 도달하기 위한 최적의 가속 매개변수를 정의했습니다 [6]. 건전한 주조 공정을 달성하기 위해서는 플런저 속도와 가속 프로파일을 신중하게 선택해야 합니다. Figure 2는 이 주장을 설명합니다. 플런저가 시스템의 임계 속도 이하로 작동하면 공기-용탕 계면, 즉 파동이 플런저에서 분리되어 챔버 내부에서 자유롭게 전파됩니다. 이는 최종 용탕 선단 뒤에 공기를 가두어 주물 내부에 결함을 유발할 수 있으므로 피해야 합니다. 두 가지 극단적인 경우가 figure 3에 추가로 나와 있습니다. Figure 3(a)는 플런저 속도가 챔버 내 축적파가 자연스럽게 전파하려는 속도보다 훨씬 느린 공정 설정을 보여줍니다. Figure 3(b)는 다른 극단적인 경우를 보여주는데, 여기서 플런저는 너무 빠르게 전파되어 파동이 부서집니다. 이러한 그림들은 각 용탕 높이와 숏 슬리브 직경 조합에 대해 찾아야 할 단 하나의 적절한 속도가 있음을 나타냅니다.

4. 연구 요약:

연구 주제의 배경:

고압 다이캐스팅(HPDC) 공정은 플런저가 숏 슬리브를 통해 용탕을 밀어내는 중요한 첫 번째 단계를 포함합니다. 이 "저속 구간" 동안의 플런저 속도는 공기 혼입 및 최종 주물 품질에 상당한 영향을 미칩니다. 결함을 최소화하기 위해서는 최적의 플런저 속도인 "임계 속도"를 결정하는 것이 중요합니다.

이전 연구 현황:

이전 연구에는 숏 슬리브 내 임계 속도 및 파동 역학 결정을 위한 해석 모델 [5, 6], 이 속도를 측정한 실험 연구 [7], 그리고 Garber [29]의 최적 속도 및 충전율에 대한 연구가 포함됩니다. Korti와 Aboudi [21]의 연구와 같은 CFD 시뮬레이션 또한 용탕/공기 계면 역학 연구에 사용되었습니다.

연구 목적:

본 논문은 오픈 소스 소프트웨어(OpenFOAM)를 사용한 CFD 방법을 통해 HPDC의 저속 구간에서 임계 플런저 속도를 조사하는 것을 목표로 합니다. 목표는 다음과 같습니다:

• 숏 슬리브 내 2상(용탕-공기) 유동에 대한 CFD 모델 개발 및 검증.
• 이동하는 플런저 처리를 위한 다양한 메쉬 이동 전략 비교.
• 매개변수 연구를 통해 2D 메쉬를 사용하여 최적 플런저 속도 결정.
• 인게이트 시스템을 포함한 실제 3D 형상의 결과와 2D 결과의 일치성 논의.

핵심 연구:

본 연구의 핵심은 다음과 같습니다:

• 공기를 압축성 이상 기체로 취급하고 난류를 RANS Menter SST k-ω 모델로 처리하는 오일러리안 유체 체적법(VOF) 접근 방식을 사용한 용탕-공기 시스템 모델링.
• 두 가지 메쉬 이동 전략(메쉬 압축 및 레이어 추가/제거) 구현 및 비교, 후자 선호.
• 개발된 솔버를 해석 모델(예: Reikher 및 Barkhudarov [27], 천수 방정식 [28]) 및 기존 CFD 데이터 [21]에 대해 검증.
• 플런저 속도와 갇힌 공기 사이의 관계를 식별하여 최적 속도 범위를 결정하기 위한 2D 숏 슬리브 모델에 대한 매개변수 연구 수행.
• 검증된 솔버를 3D 산업용 숏 슬리브 형상(EA211 크랭크 케이스)에 적용하여 보다 현실적인 시나리오에서 성능을 평가하고 결과를 확인.

5. 연구 방법론

연구 설계:

본 연구는 전산 유체 역학(CFD) 시뮬레이션 접근 방식을 사용했습니다. 연구에는 이동하는 플런저를 통합하여 HPDC 숏 슬리브 내의 2상(용탕 및 공기) 압축성 유동 모델링이 포함되었습니다. 연구 설계는 다음을 포함합니다:

• OpenFOAM을 사용한 CFD 모델 개발.
• 확립된 해석 모델 및 이전에 발표된 실험 및 CFD 결과에 대한 수치 솔버 검증.
• 플런저 속도가 공기 혼입에 미치는 영향을 조사하기 위한 매개변수 연구.
• 2D 단순화 형상 및 3D 실제 산업 사례 모두에 모델 적용.

데이터 수집 및 분석 방법:

데이터는 개발된 OpenFOAM 솔버를 사용한 수치 시뮬레이션을 통해 생성되었습니다. 분석된 주요 변수는 다음과 같습니다:

• 용탕 선단이 인게이트에 도달했을 때 숏 슬리브에 갇힌 공기의 양.
• 숏 슬리브 내 용탕 선단의 거동 및 파동 전파.
• 플런저에서의 용탕 높이.
  다양한 플런저 속도에 대해 시뮬레이션이 실행되었습니다. 분석은 공기 혼입을 유발하는 유동 패턴을 식별하고 이를 최소화하는 최적 속도 범위를 결정하는 데 중점을 두었습니다. 메쉬 이동 전략은 안정성 및 계산 효율성에 대해 비교되었습니다.

연구 주제 및 범위:

주요 연구 주제는 공기 혼입을 최소화하기 위한 HPDC 공정의 저속 구간에서 임계 플런저 속도를 결정하는 것이었습니다. 범위는 다음을 포함합니다:

• 압축성 2상 유동(액체 알루미늄 합금 및 공기) 모델링.
• 이동하는 플런저와 관련된 유체-구조 상호작용 시뮬레이션.
• 메쉬 이동 전략(메쉬 압축 대 레이어 제거) 조사 및 비교.
• CFD 솔버 검증.
• 2D 숏 슬리브 형상(예: 130mm 직경, 65% 충전율)에 대한 매개변수 연구.
• 인게이트 시스템을 포함한 3D 산업용 숏 슬리브 형상(Volkswagen의 EA211 크랭크 케이스)에 대한 솔버 적용 및 테스트.

6. 주요 결과:

주요 결과:

• 본 연구는 무료로 사용 가능한 오픈 소스 소프트웨어(OpenFOAM)가 HPDC 숏 슬리브 저속 구간의 복잡한 유동 역학을 효과적으로 모델링할 수 있음을 보여주었습니다.
• "레이어 추가 및 제거" 메쉬 이동 전략이 메쉬 압축에 비해 시뮬레이션에 더 안정적이고 계산적으로 효율적인 것으로 밝혀졌습니다.
• 개발된 CFD 솔버는 Reikher와 Barkhudarov [27]의 모델(천수 방정식 [28]에서 파생된 방정식 (19))과 같은 해석 모델 및 Korti와 Aboudi [21]의 이전에 발표된 CFD 데이터(Figure 7)에 대해 성공적으로 검증되었습니다.
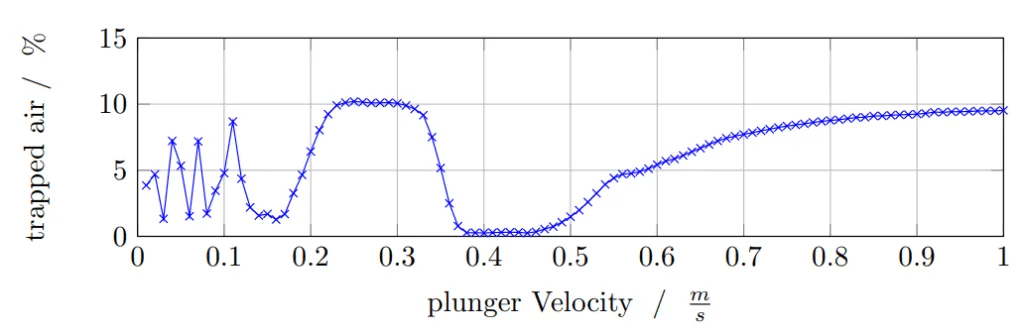
• 2D 숏 슬리브(직경 130mm, 충전율 65%, 길이 1.015m)의 경우, 매개변수 연구를 통해 약 0.38ms⁻¹ ~ 0.46ms⁻¹의 최적 플런저 속도 범위가 확인되었습니다(Figure 10). 이 범위는 갇힌 공기를 최소화하며, 유사한 구성에 대해 0.46ms⁻¹를 임계 속도로 보고한 Garber [29] 및 Brunnhuber [2]의 실험 데이터와 잘 일치합니다.
• 플런저 속도에 따라 다음과 같은 다양한 유동 영역이 확인되었습니다:
  • 너무 느림(< ~0.17 ms⁻¹): 불안정한 파동 운동, 큰 공기 포켓 가능성.
  • 중간 정도로 느림(~0.23 ms⁻¹ - 0.32 ms⁻¹): 완전한 파동 이동에는 피스톤이 너무 빨라 용탕이 갇힘.
  • 최적 범위(~0.38 ms⁻¹ - 0.46 ms⁻¹): 파동 정점이 숏 슬리브 천장까지 쌓여 공기를 효과적으로 밀어냄.
  • 너무 빠름(> 0.46 ms⁻¹): 용탕이 축적되고 파동이 부서져 공기를 혼입시킴.
• 플런저를 정확한 임계 속도보다 약간 빠르게 작동하는 것이 너무 느리게 작동하여 용탕 선단 뒤에 큰 고립된 공기 포켓을 유발하는 것보다 (공기 혼입 측면에서) 덜 해롭다는 것이 관찰되었습니다.
• 솔버는 특정 인게이트 시스템을 포함한 3D 산업용 숏 슬리브 형상(EA211 크랭크 케이스)에 성공적으로 적용되었습니다. 결과(Figure 11, Figure 12)는 첫 번째 단계에서 플런저 속도를 최적 속도로 증가시키면 용탕 선단 뒤에 갇힌 공기가 지속적으로 감소함을 확인했습니다.

그림 이름 목록:

• Figure 1: 다이 충전의 세 단계.
• Figure 2: [1]에 따른 플런저 전파 증가의 영향.
• Figure 3: 고압 다이캐스팅 공정의 첫 번째 단계 동안 잘못된 플런저 속도의 두 가지 극단적인 경우.
• Figure 4: t = 0에서의 기본 메쉬의 단순화된 그림.
• Figure 5: Δt 간격이 경과하고 압축 전략이 사용된 후의 메쉬의 단순화된 그림.
• Figure 6: 메쉬 이동 절차 중 레이어 제거 과정.
• Figure 7: 제시된 OpenFOAM 모델과 Korti 및 Aboudi [21]의 이전에 발표된 데이터와의 벤치마킹; 그림은 다양한 시간 단계에서의 계면 위치를 보여줍니다.
• Figure 8: 2상 VOF 솔버의 해결 과정 개요도.
• Figure 9: 피스톤 경계에서의 용탕 높이; [27]에 따른 해석 모델 대 수치 시뮬레이션 결과.
• Figure 10: 0과 1 m/s 사이의 저속 구간 속도에 대한 숏 슬리브 내부의 갇힌 공기 비율; 표 3에 따른 매개변수.
• Figure 11: EA211 크랭크 케이스 적용을 위한 숏 슬리브의 갇힌 공기 및 해당 테스트된 플런저 법칙.
• Figure 12: 용탕 선단이 인게이트로 전파된 후 공기가 차지하는 비율.

7. 결론:

본 논문의 연구는 고가의 상용 소프트웨어 도구 없이도 무료로 사용 가능한 오픈 소스 소프트웨어를 사용하여 저속 구간에서 숏 슬리브 역학의 계산적으로 다소 복잡한 유동 문제를 모델링할 수 있음을 보여주었습니다. 문서화된 결과는 해당 문제에 대한 이전 CFD 시뮬레이션 및 천수 방정식에서 파생된 해석 모델과 잘 일치합니다. 레이어 제거 접근 방식을 선호하는 두 가지 다른 메쉬 이동 전략이 제시되었습니다. 솔버는 궁극적으로 일반적인 산업용 인게이트 시스템이 부착된 3D 숏 슬리브의 용탕 유동을 해결할 수 있었습니다. 실제 테스트에서 3D 형상에 대해 예상되는 결과를 재현하는 것이 일반적으로 가능했습니다. 공기 혼입 감소를 위해 피스톤 운동의 저속 구간에서 속도를 증가시키는 경제적 이점 또한 지적되었습니다.

8. 참고문헌:

• [1] B. Nogowizin, Theorie und Praxis des Druckgusses, Schiele und Schoen, Berlin, 1st edn., ISBN 978-3794907960, 2010.
• [2] E. Brunnhuber, Praxis der Druckgussfertigung, Schiele und Schoen, Berlin, ISBN 978-3794905355, 1991.
• [3] H. Kaufmann, P. Uggowitzer, Metallurgy and processing of high-integrity light metal pressure castings, Fachverlag Schiele & Schön, 2014.
• [4] J. Campbell, Complete Casting Handbook: Metal Casting Processes, Metallurgy, Techniques and Design, Elsevier Science, ISBN 9780081001202, 2015.
• [5] J. López, J. Hernández, F. Faura, G. Trapaga, Shot sleeve wave dynamics in the slow phase of die casting injection, Journal of fluids engineering 122 (2) (2000) 349-356.
• [6] F. Faura, J. López, J. Hernández, On the optimum plunger acceleration law in the slow shot phase of pressure die casting machines, International Journal of Machine Tools and Manufacture 41 (2) (2001) 173–191.
• [7] T. Tszeng, Y. Chu, A study of wave formation in shot sleeve of a die casting machine, Journal of engineering for industry 116 (2) (1994) 175–182.
• [8] C. Hirt, B. Nichols, Volume of fluid (VOF) method for the dynamics of free boundaries, J. Comp. Phys. 39 (1981) 201-225.
• [9] A. Dahle, L. Arnberg, The rheological properties of solidifying aluminum foundry alloys, JOM 48 (3) (1996) 34-37.
• [10] P. Ferrer, D. Causon, L. Qian, C. Mingham, Z. Ma, A multi-region coupling scheme for compressible and incompressible flow solvers for two-phase flow in a numerical wave tank, Computers & Fluids 125 (2016) 116–129.
• [11] R. Mayon, Z. Sabeur, M.-Y. Tan, K. Djidjeli, Free surface flow and wave impact at complex solid structures, in: 12th International Conference on Hydrodynamics, Egmond aan Zee, NL, 18-23 September, 10pp., 2016.
• [12] S. Kohlstädt, M. Vynnycky, A. Neubauer, A. Gebauer-Teichmann, Comparative RANS turbulence modelling of lost salt core viability in high pressure die casting, accepted for publication in Prog. Comp. Fluid Dyn., 2018.
• [13] J. Brackbill, D. Kothe, C. Zemach, A continuum method for modeling surface tension 100 (2) (1992) 335-354.
• [14] H. Rusche, Computational fluid dynamics of dispersed two-phase flows at high phase fractions, Ph.D. thesis, Imperial College London (University of London), 2003.
• [15] H. Versteeg, W. Malalasekera, An Introduction to Computational Fluid Dynamics: The Finite Volume Method, Pearson Education Limited, 2007.
• [16] F. Menter, 2-equation eddy-viscosity turbulence models for engineering applications, AIAA J. 32 (1994) 1598–1605.
• [17] E. Robertson, V. Choudhury, S. Bhushan, D. Walters, Validation of OpenFOAM numerical methods and turbulence models for incompressible bluff body flows, Computers & Fluids 123 (2015) 122-145.
• [18] F. Menter, M. Kuntz, R. Langtry, Ten years of industrial experience with the SST turbulence model, Turbulence, Heat and Mass Transfer 4 (1) (2003) 625-632.
• [19] M. Koch, C. Lechner, F. Reuter, K. Köhler, R. Mettin, W. Lauterborn, Numerical modeling of laser generated cavitation bubbles with the finite volume and volume of fluid method, using OpenFOAM, Computers & Fluids 126 (2016) 71-90.
• [20] F. White, Fluid mechanics, in SI units, McGraw-Hill, 2011.
• [21] A. Korti, S. Abboudi, Numerical simulation of the interface molten metal air in the shot sleeve chambre and mold cavity of a die casting machine, Heat and Mass Transfer 47 (11) (2011) 1465-1478.
• [22] H. Jasak, A. Jemcov, Z. Tukovic, OpenFOAM: A C++ Library for Complex Physics Simulations, in: International Workshop on Coupled Methods in Numerical Dynamics IUC, 2007.
• [23] H. Weller, G. Tabor, H. Jasak, C. Fureby, A tensorial approach to computational continuum mechanics using object orientated techniques, Computers in Physics 12(6) (1998) 620-631.
• [24] H. Jasak, OpenFOAM: open source CFD in research and industry, International Journal of Naval Architecture and Ocean Engineering 1 (2) (2009) 89-94.
• [25] S. Patankar, D. Spalding, A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows, in: Numerical Prediction of Flow, Heat Transfer, Turbulence and Combustion, Elsevier, 54-73, 1983.
• [26] R. Issa, Solution of the implicitly discretised fluid flow equations by operator-splitting, Journal of Computational Physics 62 (1) (1986) 40–65.
• [27] A. Reikher, M. Barkhudarov, Casting: an analytical approach, Springer Science & Business Media, 2007.
• [28] M. Castro, M. Semplice, Third-and fourth-order well-balanced schemes for the shallow water equations based on the CWENO reconstruction, International Journal for Numerical Methods in Fluids 89 (8) (2019) 304-325.
• [29] L. Garber, Theoretical analysis and experimental observation of air entrapment during cold chamber filling, Die Casting Engineer 26 (3) (1982) 14-15.

9. 저작권:

• 이 자료는 "S. Kohlstädt, M. Vynnycky, S. Goeke, A. Gebauer-Teichmann"의 논문입니다. "On determining the critical velocity in the high-pressure die casting machine's shot sleeve using CFD"를 기반으로 합니다.
• 논문 출처: [DOI URL 자리 표시자 - 2019년 4월 25일 Elsevier에 제출된 프리프린트이므로, 가능해지면 추가 예정]

이 자료는 위 논문을 바탕으로 요약되었으며, 상업적 목적의 무단 사용을 금합니다.
Copyright © 2025 CASTMAN. All rights reserved.

연구자를 위한 주요 질문 및 답변

Q1. HPDC 숏 슬리브 저속 구간에서 임계 속도를 결정하는 주된 목적은 무엇입니까?

A1. 주된 목적은 숏 슬리브 내부의 공기가 용탕 선단보다 앞서 효과적으로 밀려나가도록 하여 용탕 내 공기 혼입을 최소화하고, 이를 통해 최종 주물의 품질을 향상시키는 것입니다 (Figure 3 및 Figure 10의 맥락에서 논의됨).

Q2. 숏 슬리브 내 용탕-공기 시스템에 어떤 CFD 모델링 접근 방식이 사용되었습니까?

A2. 본 연구는 용탕-공기 시스템을 모델링하기 위해 오일러리안 유체 체적법(VOF) 접근 방식을 사용했습니다. 공기는 압축성 이상 기체로 취급되었고, 난류는 Menter SST k-ω 모델을 사용하는 RANS 접근 방식으로 처리되었습니다 (초록, 섹션 2).

Q3. 본 연구에서 개발된 CFD 솔버는 어떻게 검증되었습니까?

A3. 솔버는 용탕 높이에 대한 Reikher와 Barkhudarov [27]의 모델(Figure 9)과 같은 해석 모델 및 계면 위치에 대한 Korti와 Aboudi [21]의 이전에 발표된 CFD 데이터(Figure 7)와 시뮬레이션 결과를 비교하여 검증되었습니다.

Q4. 연구된 특정 2D 숏 슬리브 사례(직경 130mm, 충전율 65%, 길이 1.015m)에 대해 확인된 최적 플런저 속도 범위는 무엇이었습니까?

A4. 최적 플런저 속도 범위는 약 0.38 ms⁻¹에서 0.46 ms⁻¹로 밝혀졌습니다. 이 범위는 갇힌 공기를 최소화했으며 Garber [29]와 Brunnhuber [2]의 실험 데이터와 일치합니다 (섹션 5.1, Figure 10).

Q5. 플런저 속도가 최적 임계 속도에서 크게 벗어나면 어떤 결과가 발생합니까?

A5. 플런저가 너무 느리게 움직이면 파동이 플런저에서 분리되어 자유롭게 전파되어 용탕 선단 뒤에 큰 공기 포켓을 가둘 수 있습니다. 플런저가 너무 빠르게 움직이면 용탕이 빠르게 축적되어 파동이 부서지고 용탕에 공기를 혼입시킵니다 (Figure 3, 섹션 5.1).

Q6. 2D 시뮬레이션 결과가 더 복잡한 3D 산업 형상에도 적용 가능했습니까?

A6. 예, 본 연구는 솔버와 임계 속도에 대한 이해가 산업용 인게이트 시스템을 포함한 실제 3D 숏 슬리브(EA211 크랭크 케이스)에 적용될 수 있음을 보여주었습니다. 3D 시뮬레이션은 최적 속도 근처에서 작동하면 갇힌 공기가 감소함을 확인했습니다 (섹션 5.2, Figure 11, Figure 12).