A Probabilistic Approach in Failure Modellingof AluminiumHighPressure Die-Castings

본 기술 요약은 Octavian Knoll이 2015년 노르웨이 과학기술대학교(NTNU) 및 카를스루에 공과대학교(KIT)에서 발표한 박사학위 논문 "A Probabilistic Approach in Failure Modelling of Aluminium High Pressure Die-Castings"을 기반으로 합니다. CASTMAN이 AI의 도움을 받아 기술 전문가를 위해 분석하고 요약했습니다.

키워드

• 주요 키워드: HPDC 고장 모델링
• 보조 키워드: 알루미늄 다이캐스팅, 주조 결함, 파괴 확률, 와이블 분포, 유한요소해석, Castasil-37

Executive Summary

바쁜 전문가를 위한 30초 요약.

• 문제점: HPDC 알루미늄 부품의 기계적 물성, 특히 연성은 주조 결함으로 인해 예측 불가능한 편차를 보입니다.
• 연구 방법: 본 연구는 특정 HPDC 부품에서 채취한 시편의 광범위한 인장 시험과 통계 분석을 통해 고장 메커니즘을 분석하고, 이를 바탕으로 확률론적 고장 모델을 개발했습니다.
• 핵심 돌파구: 부품 내 연성 변화는 주조 시스템에 따른 '전역적 체계적 변화'와 공정 변동에 따른 '국부적 준-무작위적 변화'로 구분되며, 후자는 와이블(Weibull) 분포로 정확하게 모델링할 수 있음을 입증했습니다.
• 핵심: 단일 유한요소 시뮬레이션으로 부품의 파괴 확률을 정확히 예측할 수 있어, 기존 몬테카를로 방식 대비 개발 시간과 비용을 획기적으로 절감할 수 있습니다.

문제점: 이 연구가 HPDC 전문가에게 중요한 이유

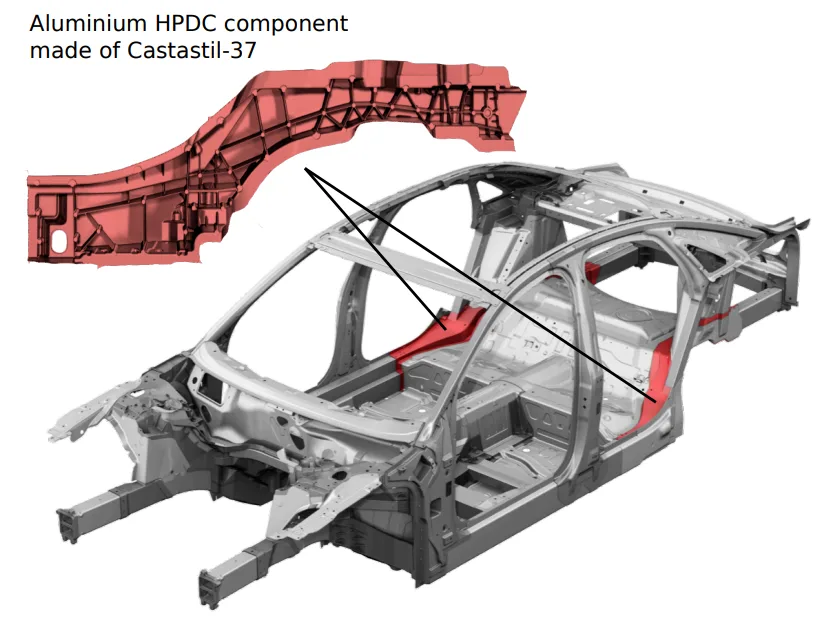
현대 자동차 산업의 핵심 과제는 경량화를 통한 연비 향상과 안전성 강화입니다. 알루미늄 고압 다이캐스팅(HPDC)은 복잡한 형상의 경량 부품을 일체형으로 생산할 수 있어 차체 설계의 필수 요소로 자리 잡았습니다. 특히 충돌 시 높은 하중을 견뎌야 하는 구조용 연결 부품에 널리 사용됩니다.

하지만 HPDC 공정의 본질적인 특성상 수축 기공, 가스 기공, 산화막과 같은 미세한 주조 결함이 발생하며, 이는 부품의 연성(ductility)에 큰 영향을 미칩니다. 문제는 이러한 결함의 분포가 부품 내에서 균일하지 않아 연성이 위치에 따라 크게 달라지고, 심지어 동일한 위치에서 생산된 부품 간에도 상당한 편차(scatter)를 보인다는 점입니다. 이러한 예측 불가능성은 부품의 신뢰성을 보장하는 데 가장 큰 걸림돌이며, 특히 충돌 안전성 설계에 있어 심각한 문제를 야기합니다. 기존의 결정론적(deterministic) 해석 방법으로는 이러한 통계적 편차를 제대로 반영할 수 없어, 과도하게 보수적인 설계를 하거나 잠재적인 파괴 위험을 안고 가야 했습니다.

연구 접근법: 방법론 분석

본 연구는 이러한 문제를 해결하기 위해 실제 산업 환경을 모사한 체계적인 실험과 분석을 수행했습니다.

연구진은 AlSi9Mn 합금(Castasil-37)으로 제작된 U자형 제네릭 HPDC 부품을 분석 대상으로 삼았습니다. 이 부품은 실제 자동차 부품처럼 얇은 벽, 리브, 이젝터 돔 등 복잡한 형상을 포함하고 있습니다.

핵심적인 접근법은 부품 내 위치에 따른 물성 변화를 파악하는 것이었습니다. 이를 위해 연구진은 여러 개의 동일한 U자형 부품에서, 주물 용탕이 주입되는 게이팅(gating) 측, 진공이 적용되는 진공(vacuum) 측, 그리고 그 사이 중간 부분 등 다양한 위치에서 수많은 인장 시험 시편을 채취했습니다.

이렇게 채취된 시편들로 준정적(quasi-static) 인장 시험을 수행하여 응력-변형률 곡선과 파괴 변형률을 측정했습니다. 수집된 방대한 데이터는 와이블 분포 분석, 가설 검정 등 엄격한 통계적 기법을 통해 분석되었습니다. 이 과정을 통해 부품 내 연성 변화의 두 가지 주요 패턴, 즉 전역적 체계적 변화와 국부적 준-무작위적 변화를 명확히 구분하고 정량화할 수 있었습니다.

핵심 돌파구: 주요 연구 결과 및 데이터

결과 1: 연성 변화의 두 가지 패턴 규명

실험 결과, 부품의 연성은 예측 가능한 패턴과 예측 불가능한 패턴이 혼재되어 나타남이 확인되었습니다.
- 전역적 체계적 변화: 주조 시스템의 영향으로, 게이팅 채널에 가까운 부위에서 채취한 시편들이 진공 채널에 가까운 부위의 시편들보다 전반적으로 더 높은 연성을 보였습니다. 이는 용탕의 유동 및 응고 과정이 부품의 거시적인 영역에 걸쳐 체계적인 품질 차이를 유발함을 의미합니다.
- 국부적 준-무작위적 변화: 동일한 위치에서 채취한 시편들 사이에서도 파괴 변형률이 큰 편차를 보였습니다. 이는 공정 중 발생하는 미세한 변동이 국부적인 결함 분포에 영향을 미쳐 발생하는 준-무작위적 현상입니다. 본 연구는 이러한 국부적 편차를 와이블(Weibull) 분포를 통해 매우 정확하게 통계적으로 모델링할 수 있음을 입증했습니다.

결과 2: 단일 시뮬레이션을 통한 파괴 확률 예측 모델 검증

연구의 가장 큰 성과는 이러한 통계적 특성을 반영한 확률론적 고장 모델을 개발하고 검증한 것입니다. 연구진은 Cockcroft-Latham 파괴 기준과 와이블 분포를 결합한 모델을 유한요소해석(FEA) 소프트웨어인 LS-DYNA의 사용자 정의 재료 모델(User-defined Material Routine)로 구현했습니다.

• 직접 계산법(MR#1): 이 모델은 단 한 번의 시뮬레이션 실행으로 부품 전체 또는 특정 부위의 파괴 확률을 변형률의 함수로 직접 계산합니다.
• 몬테카를로 시뮬레이션(MR#2): 수십 번의 반복 시뮬레이션을 통해 통계적으로 파괴 확률을 추정하는 기존 방식입니다. 각 시뮬레이션마다 와이블 분포에 따라 무작위로 파괴 임계값을 할당합니다.

Figure 10.1.4에서 볼 수 있듯이, 단일 시뮬레이션(MR#1, 파란색 실선)으로 예측한 파괴 확률 곡선은 36번의 몬테카를로 시뮬레이션(MR#2, 파란색 삼각형)으로 추정한 결과와 거의 완벽하게 일치했습니다. 이는 막대한 계산 비용과 시간이 소요되는 몬테카를로 시뮬레이션을 단 한 번의 시뮬레이션으로 대체할 수 있음을 의미하며, HPDC 부품의 신뢰성 해석에 있어 획기적인 효율성 향상을 가져올 수 있습니다.

R&D 및 운영을 위한 실질적 시사점

• 공정 엔지니어: 본 연구는 주조 시스템이 부품의 전역적 품질 분포에 미치는 영향을 명확히 보여줍니다. 주조 시뮬레이션(예: MAGMAsoft) 결과를 활용하여 연성이 낮을 것으로 예상되는 영역을 사전에 파악하고, 게이팅 및 진공 시스템 설계를 최적화하여 부품 전반의 품질 균일성을 높이는 데 기여할 수 있습니다.
• 품질 관리팀: 와이블 분포 모델은 단순한 평균값 기반의 합격/불합격 판정을 넘어, 제품의 신뢰도를 확률적으로 관리할 수 있는 새로운 기준을 제시합니다. 특정 위치에서 측정된 물성 데이터의 통계적 분포를 분석하여 공정 안정성을 평가하고, 잠재적 불량률을 예측하는 데 활용할 수 있습니다.
• 설계 엔지니어: 확률론적 고장 모델을 통해 '허용 파괴 확률' 기반의 신뢰성 설계(reliability-based design)가 가능해집니다. 이는 최소 물성치에 기반한 과도한 안전율 설계를 피하고, 부품의 무게와 성능을 최적화하면서도 목표 신뢰도를 달성하는 데 핵심적인 역할을 합니다. 특히, 주조 시뮬레이션 결과와 연계한 '재료 카드 매핑(material card mapping)' 기법을 적용하면 부품의 위치별 특성을 설계 단계에서부터 정밀하게 반영할 수 있습니다.

논문 상세 정보

A Probabilistic Approach in Failure Modelling of Aluminium High Pressure Die-Castings

1. 개요:

• 제목: A Probabilistic Approach in Failure Modelling of Aluminium High Pressure Die-Castings
• 저자: Octavian Knoll
• 발행 연도: 2015
• 학술지/학회: PhD Thesis, Norwegian University of Science and Technology (NTNU) & Karlsruhe Institute of Technology (KIT)
• 키워드: Aluminium, High Pressure Die-Casting, Failure Modelling, Probabilistic Approach, Weibull Distribution, Finite Element Method

2. 초록:

알루미늄 고압 다이캐스팅(HPDC) 부품의 연성은 주조 결함에 의해 크게 영향을 받으며, 이는 부품 내에서 전역적 체계적 변화와 국부적 준-무작위적 변화를 야기한다. 본 연구는 AlSi9Mn 합금으로 제작된 제네릭 HPDC 부품의 광범위한 인장 시험을 통해 이러한 두 가지 변화를 실험적으로 분석했다. 시험 결과, 변형 경화 거동은 재현성이 높았으나 파괴 변형률은 위치에 따라 큰 편차를 보였다. 통계 분석을 통해 부품을 유사한 연성을 가진 특성 부위로 나눌 수 있었으며, 국부적 준-무작위적 변화는 와이블(Weibull) 분포로 설명될 수 있음을 보였다. 이 결과를 바탕으로, Cockcroft-Latham 파괴 기준과 와이블 모델을 결합한 확률론적 고장 모델을 개발했다. 이 모델을 통해 단일 유한요소 시뮬레이션으로 파괴 확률을 직접 계산하는 접근법을 제시했으며, 이는 몬테카를로 시뮬레이션 결과와 동일한 예측 정확도를 보였다. 굽힘 및 압축 시험을 통해 모델의 유효성을 검증했으며, 실험적으로 추정된 파괴 확률과 높은 상관관계를 보였다.

3. 서론:

현대 자동차 차체 설계는 경량화와 구조 강성 및 충돌 안전성 향상을 목표로 한다. 알루미늄 HPDC 부품은 복잡한 형상의 구조 연결 부품을 일체형으로 제작할 수 있어 이러한 요구를 충족시키는 핵심 기술이다. 그러나 HPDC 공정에서 발생하는 주조 결함은 재료의 연성에 큰 편차를 유발하여, 특히 충돌 상황에서 부품의 신뢰성을 예측하기 어렵게 만든다. 따라서 유한요소법을 이용한 정확한 수치 해석을 위해서는 주조 결함으로 인한 연성의 변화를 고려한 신뢰성 있는 재료 모델이 필수적이다. 본 연구는 Audi A8 차체에 사용된 Castasil-37 합금 부품을 모티브로 하여, 주조 상태 그대로 사용되는 HPDC 부품의 변형 및 파괴 거동을 정확하게 예측할 수 있는 수치 모델 개발을 목표로 한다.

4. 연구 요약:

연구 주제의 배경:

HPDC 부품은 자동차 산업에서 구조적 노드 및 커넥터 요소로 널리 사용되며, 높은 하중을 견뎌야 한다. 그러나 주조 결함으로 인한 연성의 불확실성은 부품의 구조적 신뢰도를 저해하는 주요 요인이다.

기존 연구 현황:

기존의 HPDC 고장 모델링 연구는 주로 결정론적 접근법에 의존하여 평균적인 물성치를 사용했기 때문에, 실제 부품에서 나타나는 큰 편차를 제대로 반영하지 못했다. 일부 확률론적 접근이 시도되었으나, 전역적 변화와 국부적 변화를 체계적으로 분리하여 분석하고 이를 실제 부품 시험으로 검증한 연구는 부족했다.

연구 목적:

본 연구의 핵심 목적은 HPDC 알루미늄 합금의 변형 및 파괴 거동을 정확하게 예측할 수 있는 수치 재료 모델을 개발하는 것이다. 특히, 주조 결함으로 인한 연성의 (1) 전역적 체계적 변화와 (2) 국부적 준-무작위적 변화를 실험적으로 분석하고, 이를 모두 고려할 수 있는 확률론적 고장 모델을 개발 및 검증하고자 한다.

핵심 연구:

1. 제네릭 HPDC 부품의 굽힘 및 압축 시험을 통해 구조적 거동과 파괴 모드의 편차를 분석.
2. 부품의 여러 위치에서 채취한 시편으로 광범위한 인장 시험을 수행하여 재료 연성의 전역적/국부적 변화를 정량화.
3. 통계적 가설 검정을 통해 재료 특성이 유사한 영역을 구분하고, 국부적 편차를 와이블 분포로 모델링.
4. Cockcroft-Latham 파괴 기준과 와이블 분포를 결합한 확률론적 고장 모델을 개발하고, 4가지 변형(MR#1~MR#4)으로 FEA 사용자 재료 모델에 구현.
5. 인장 시험 및 부품 시험의 수치 시뮬레이션을 통해 개발된 모델의 정확성과 효율성을 검증.

5. 연구 방법론

연구 설계:

실제 부품의 복잡한 거동을 모사하기 위해 제네릭 U자형 HPDC 부품(U900-1, Castasil-37 합금)을 대상으로 실험적 분석과 수치적 모델링을 결합한 연구를 설계했다. 실험은 부품 수준의 구조 시험과 재료 수준의 물성 시험으로 구성되었다.

데이터 수집 및 분석 방법:

• 데이터 수집: 3점 굽힘 시험과 축 방향 압축 시험을 통해 부품의 하중-변위 곡선과 파괴 거동을 수집했다. 재료 물성은 부품의 15개 다른 위치에서 채취한 총 75개의 UT80 시편과, 3개 주요 부위에서 채취한 216개의 UT75 및 UT117 시편에 대한 인장 시험을 통해 수집되었다.
• 데이터 분석: 수집된 데이터는 기술 통계, 상자 그림(box-plot), 가설 검정(F-test, t-test, KS-test), 앤더슨-달링 적합도 검정(Anderson-Darling GoF test) 등 다양한 통계 기법으로 분석되었다. 특히, 파괴 임계값(Wc)의 분포는 와이블 확률도를 이용하여 분석되었다.

연구 주제 및 범위:

연구는 AlSi9Mn(Castasil-37) 합금의 주조 상태(F)에서의 준정적 인장 파괴 거동에 초점을 맞춘다. 재료 특성화는 부품 내 연성의 공간적 분포와 국부적 편차를 분석하는 데 중점을 둔다. 수치 모델링은 등방성 탄소성 구성 모델과 확률론적 파괴 기준을 결합하며, 그 유효성은 인장 시험 및 부품 시험 시뮬레이션을 통해 검증된다.

6. 주요 결과:

주요 결과:

• HPDC 부품의 연성은 게이팅 측에서 진공 측으로 갈수록 감소하는 '전역적 체계적 변화'와, 동일 위치 내에서도 큰 편차를 보이는 '국부적 준-무작위적 변화'를 동시에 나타낸다.
• 국부적 연성 편차는 정규 분포보다 와이블 분포로 더 잘 설명된다.
• 단일 FE 시뮬레이션으로 파괴 확률을 직접 계산하는 방법(MR#1)은 다수의 시뮬레이션이 필요한 몬테카를로 방법(MR#2)과 동일한 수준의 예측 정확도를 보였다.
• 분리된 모델링 접근법(Uncoupled approach, MR#3)을 사용하면 재료의 통계적 특성을 유지하면서 FE 메쉬 수렴성 연구를 수행할 수 있어, 기존 결합 모델(Coupled approach, MR#2)의 한계를 극복할 수 있다.
• 개발된 확률론적 고장 모델은 3점 굽힘 및 축 방향 압축 부품 시험에서 실험적으로 측정된 파괴 확률 분포와 높은 상관관계를 보이며 성공적으로 검증되었다.

그림 제목 목록:

• Figure 1.1.1: Application of two high pressure die-casting components made of the aluminium alloy Castasil-37 in the car body of the current Audi A8 (third generation (D4), production 2010 - present).
• Figure 2.0.1: Examples of casting products made of metal, concrete and plastic.
• Figure 2.1.1: Aluminium HPDC gearbox of a KTM motorcycle, see Aluminium Rheinfelden GmbH [6].
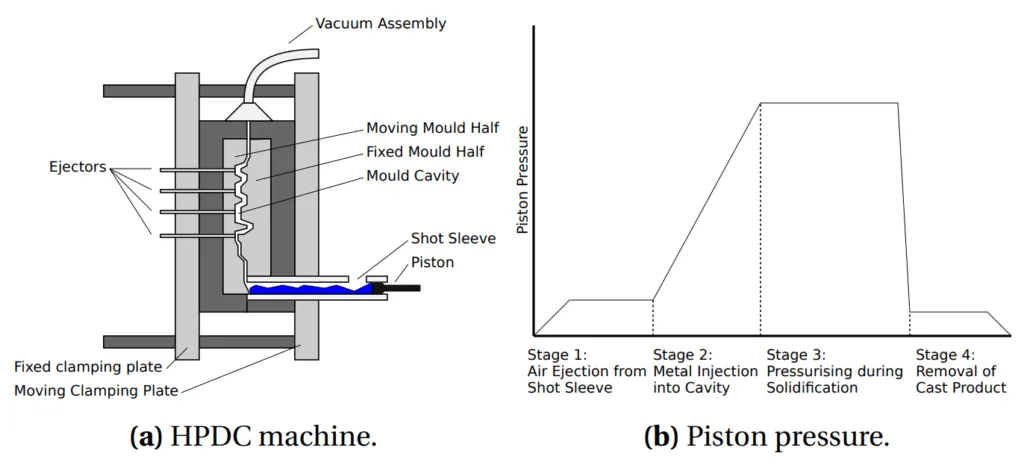
• Figure 2.1.2: Exemplary drawing of cold chamber HPDC machine with vacuum assembly and piston pressure during HPDC process.
• Figure 2.1.3: Result of an HPDC simulation preformed with MAGMAsoft, see Kleeberg [66].
• Figure 2.2.1: Characteristic phase diagrams of an Al-Si alloy and an Al-Mg alloy, see Bargel and Schulze [9].
• Figure 2.2.2: Microstructure of an HPDC Al-Si-Mg alloy, see Dørum et al. [33].
• Figure 2.3.1: Microstructure of an aluminium HPDC alloy (AlSi9Mg) containing casting defects, see Teng et al. [106].
• Figure 2.4.1: Car body of the current Audi A8 (third generation (D4), production 2010 - present): Application of aluminium sheets (green), aluminium extrusions (blue) and aluminium die-castings (red).
• Figure 3.2.1: Two events A and B taken from the sample space Ω.
• Figure 3.2.2: Bayes’ theorem.
• Figure 3.3.1: Probability Density Function (PDF) and Cumulative Distribution Function (CDF) of a discrete and a continuous random variable.
• Figure 3.3.2: Mathematical expectations and statistical measurements.
• Figure 3.3.3: Examples of uniform PDFs and CDFs (A = 1; B = 2, 4, 6).
• Figure 3.3.4: Examples of normal PDFs and CDFs (µ = 0;σ = 0.5, 1, 2).
• Figure 3.3.5: Bivariate normal distributions (σX1X2 = {0, 0.8,−0.8}).
• Figure 3.3.6: Examples of Weibull PDFs and CDFs (m = 0.5, 1, 2, 4;λ = 4).
• Figure 3.3.7: Comparison of uniform, normal and Weibull distribution with equal mean and standard deviation (µ = 3.6,σ = 1.0).
• Figure 3.3.8: Inverse transformation technique.
• Figure 3.3.9: Influence of Gaussian correlation length d0 on samples of 1D Gaussian random fields.
• Figure 3.3.10: Influence of Gaussian correlation length d0 on samples of 2D Gaussian random fields.
• Figure 3.5.1: Graphical representation of sample X and sample Y.
• Figure 3.5.2: Details of a box-plot.
• Figure 3.5.3: Distribution estimation of sample X and sample Y.
• Figure 3.6.1: Illustration of the (1 − α) · 100% confidence interval and the t-distribution.
• Figure 3.6.2: Estimated normal distribution and Weibull distribution of sample X and sample Y.
• Figure 4.1.1: Deformation measurements of a solid body.
• Figure 4.1.2: Illustration of a solid body subjected to of external loads and the Cauchy theorem.
• Figure 4.1.3: High-exponent yield surface in plane stress and two-terms Voce rule.
• Figure 4.1.4: Isotropic hypoelastic-plastic material model for metals assuming isothermal conditions.
• Figure 4.1.5: FEM applied on a structural problem.
• Figure 4.1.6: Deformation of a four node element.
• Figure 4.1.7: Discretisation of time t.
• Figure 4.1.8: Flow chart of the explicit time integration algorithm using the central differences method in the form proposed by Verlet [110].
• Figure 4.2.1: Characteristic stress-strain curves for brittle, quasi-brittle and ductile materials.
• Figure 4.2.2: Schematic representation of the fracture mechanisms in brittle and ductile materials.
• Figure 4.2.3: Stress distribution prior to fracture in a tensile test specimen.
• Figure 4.3.1: Typical specimen geometries for mechanical material tests.
• Figure 4.3.2: Schematic representation of the homogenisation procedure.
• Figure 4.3.3: Uniaxial tensile test: Tensile test set-up and experimental force-elongation curves obtained from the ductile and the quasi-brittle specimen.
• Figure 4.3.4: Numerical and experimental force-elongation curves: Comparison of the three mesh sizes le = 1.00mm, le = 0.50mm and le = 0.25mm.
• Figure 4.3.5: W distributions at the moment when the elongation of the gauge section reaches the experimental rupture elongation: Comparison of the three mesh sizes le = 1.00mm, le = 0.50mm and le = 0.25mm.
• Figure 4.3.6: Influence of mesh size le on critical value Wc and averaged critical value Wc in an experimental-numerical approach.
• Figure 5.1.1: Failure probability PΛF = 1 − e−cl plotted as function of segment length l for varying weakest-link densities c.
• Figure 5.1.2: Failure probability PVF = 1 − e−c(f)V plotted as function of material volume V with a constant value of density function c(f).
• Figure 5.1.3: Failure probability by Weibull plotted as function of uniform loading f for either varying Weibull modulus m or varying volume relation V/V0.
• Figure 5.1.4: Failure probability according to the approach by Unosson et al. [108] plotted as function of loading f.
• Figure 5.1.5: Weibull plots including a Weibull curve obtained from a small gauge volume (red) and a Weibull curve obtained from a large gauge volume (blue).
• Figure 5.1.6: Gauge parts under different loading conditions with equal gauge volumes (VT = VC = VS = VPT).
• Figure 5.2.1: Randomly distributed failure parameters: The failure parameters are uniformly distributed within the FE mesh.
• Figure 5.2.2: Range of the middle 95% of a Weibull distributed population.
• Figure 5.2.3: Randomly distributed failure parameters: The failure parameters are uniformly distributed within the MS mesh, then the MS mesh is discretised into a FE mesh.
• Figure 5.2.4: Randomly distributed failure parameters: The failure parameters are distributed within the MS mesh according to a uniform random field, then the MS mesh is discretised into a FE mesh.
• Figure 7.1.1: Images of the aluminium HPDC component U900-1.
• Figure 7.2.1: Three-point bending test set-up: Technical drawing and images of the test set-up.
• Figure 7.2.2: Deformed and fractured U900-1 component subjected to three-point bending.
• Figure 7.2.3: Experimental results obtained from seven parallel three-point bending tests (measured by the testing machine).
• Figure 7.2.4: Experimental results obtained from six parallel three-point bending tests: Force and displacement measured by testing machine and relative displacements measured by extensometers on gating side and vacuum side.
• Figure 7.2.5: Drawing of the punch rotation during three-point testing.
• Figure 7.3.1: Axial compression test set-up: Cutting pattern, technical drawing and image of the test set-up.
• Figure 7.3.2: Deformed and fractured modified U900-1 component subjected to axial compression.
• Figure 7.3.3: Experimental force-displacement curves obtained from four parallel axial compression tests (measured by the testing machine).
• Figure 7.3.4: Experimental results obtained from four parallel axial compression tests: Force and displacement measured by the testing machine and relative displacement measured by the extensometer.
• Figure 7.3.5: Drawing of the loading plate rotation during axial compression testing.
• Figure 8.1.1: Technical drawing and image of the applied uniaxial tensile test set-up.
• Figure 8.1.2: Definition of U900-1 component parts (unfolded geometry).
• Figure 8.1.3: Mechanical analysis of the result obtained from a uniaxial tensile test.
• Figure 8.1.4: Mechanical analysis of the result obtained from a uniaxial tensile test.
• Figure 8.1.5: Approach of statistical hypothesis testing of k samples Xi at a significance level of α = 0.05 using MATLAB [84].
• Figure 8.2.1: Uniaxial tensile test specimen UT80 (t = 2.5mm).
• Figure 8.2.2: Engineering stress-strain curves obtained from UT80 specimens machined from an U900-1 component (component #1).
• Figure 8.2.3: Engineering stress-strain curves obtained from UT80 specimens machined from five U900-1 components presented according to the extraction position.
• Figure 8.2.4: Averages and COVs of the measured mechanical quantities obtained from UT80 specimens machined from five U900-1 components.
• Figure 8.2.5: Engineering stress-strain curves obtained from the most ductile specimen and the least ductile specimen and scatter plots of the measured mechanical quantities obtained from UT80 specimens machined from five U900-1 components.
• Figure 8.2.6: Images of fractured UT80 specimens machined from the fifteen extraction positions of the U900-1 component.
• Figure 8.2.7: Identification of casting defects in form of porosity using CT scanning of the middle section of three U900-1 components.
• Figure 8.2.8: Identification of casting defects in form of shrinkage pores, initial cracks and other microstructural irregularities using SEM of fractured UT80 specimens machined from U900-1 components.
• Figure 8.3.1: Uniaxial tensile test specimen UT75 and uniaxial tensile test specimen UT117.
• Figure 8.3.2: Engineering stress-strain curves obtained from UT75 and UT117 specimens machined from six U900-1 components presented according to extraction positions.
• Figure 8.3.3: Average and COVs of the measured mechanical quantities obtained from UT75 and UT117 specimens machined from six U900-1 components.
• Figure 8.3.4: Scatter plots of the measured mechanical quantities obtained from UT75 and UT117 specimens machined from six U900-1 components.
• Figure 8.3.5: Measured fracture strain Af obtained from UT75 and UT117 specimens machined from six U900-1 components plotted according to extraction positions in longitudinal direction.
• Figure 8.3.6: Scatter plots of the measured fracture strain Af obtained from UT75 and UT117 specimens machined from six U900-1 components.
• Figure 8.3.7: Three fractured UT117 specimens machined from part BF of U900-1 components.
• Figure 8.3.8: Probability plot of the samples based on measurements of Wc obtained from UT75 and UT117 specimens machined from part OW of six U900-1 components and extendedly fitted Weibull probability function using a considered volume of V = VUT75 and V = VUT117 (m = 5.4829, Wc0 = 0.0206kN/mm2, V0 = 1000.0mm3).
• Figure 9.3.1: Fortran 95 code of subroutine init_random_seed(t) taken from the course “FORTRAN Programming for Engineers” by D. Hogan [94].
• Figure 9.4.1: Creation of the MS mesh based on the dimensions of the FE mesh and mapping of the MS mesh onto the FE mesh.
• Figure 10.1.1: FE model of the uniaxial tensile test using a UT80 specimen.
• Figure 10.1.2: Fitted two-terms Voce rule based on experimental hardening curves obtained from UT80 specimens machined from part OW.
• Figure 10.1.3: Comparison of predicted engineering stress-strain curve using material routine MR#1 (red) and experimental engineering stress-strain curves (grey) as well as comparison of predicted failure probability using material routine MR#1 (blue) and experimental failure probability (blue triangles).
• Figure 10.1.4: Predicted engineering stress-strain curves using material routine MR#2 (red) and comparison of predicted failure probability using material routine MR#1 (blue) and predicted failure probability using material routine MR#2 (blue triangles).
• Figure 10.1.5: Five deformed and fractured UT80 specimens obtained from FE simulations using material routine MR#2 including the pseudo-random distributions of critical value Wc (le = 1.00mm).
• Figure 10.1.6: Mesh convergence study of the FE model of the uniaxial tensile test using material routine MR#2 (le = {1.00mm, 0.50mm, 0.25mm, 0.125mm}).
• Figure 10.1.7: Uncoupled modelling approach applied on the FE model of the UT80 specimen using material routine MR#3 and material routine MR#4.
• Figure 10.1.8: Mesh convergence study of the FE model of the uniaxial tensile test using material routine MR#3 (le = {1.00mm, 0.50mm, 0.25mm, 0.125mm}).
• Figure 10.1.9: Mesh convergence study of the FE model of the uniaxial tensile test using material routine MR#4 (le = {1.00mm, 0.50mm, 0.25mm, 0.125mm}).
• Figure 10.2.1: Image of the three-point bending test set-up and experimental results.
• Figure 10.2.2: FE model of the U-profile subjected to three-point bending.
• Figure 10.2.3: Numerical results obtained from a single simulation of the U-profile subjected to three-point bending using material routine MR#1 (le = 3.00mm).
• Figure 10.2.4: Numerical results obtained from a single simulation of the U-profile subjected to three-point bending using material routine MR#2 (le = 3.00mm).
• Figure 10.2.5: Comparison of the numerical results obtained from simulations of the U-profile subjected to three-point bending using material routines MR#1 and MR#2 (le = 3.00mm).
• Figure 10.2.6: Mesh sensitivity analysis of the FE model of the U-profile subjected to three-point bending using material routine MR#3: Predicted force-displacement curves (le = {3.00mm, 1.50mm, 0.75mm, 0.38mm}).
• Figure 10.2.7: Mesh convergence study of the FE model of the U-profile subjected to three-point bending using material routine MR#3: Prediction of fracture initiation in the vacuum side (le = {3.00mm, 1.50mm, 0.75mm, 0.38mm}).
• Figure 10.2.8: Through-process modelling approach applied on the FE model of the U-profile (le = 3.00mm).
• Figure 10.2.9: Comparison of numerical results obtained from simulations (material routine MR#1) of the U-profile subjected to three-point bending without mapping and with mapping (le = 3.00mm).
• Figure 10.3.1: Discretisation of the cross-section of the U900-1 component using a solid mesh (le ≤ 1.0mm), a shell mesh (le ≤ 8.0mm) and a hybrid mesh (le ≤ 5.0mm).
• Figure 10.3.2: FE model of the small ejector dome applied for eigenfrequency analysis and numerical results of the first bending eigenfrequency ωB1 and the first torsional eigenfrequency ωT1 (solid mesh).
• Figure 10.3.3: Part definition of the U900-1 component: Gating side (blue), intermediate part (red) and vacuum side (green).
• Figure 10.3.4: Fitted two-terms Voce rules based on experimental hardening curves obtained from UT75 specimens machined from gating side (IW), intermediate part (BF) and vacuum side (OW).
• Figure 10.3.5: Numerical model of the three-point bending test set-up.
• Figure 10.3.6: Comparison of experimental results and numerical results obtained from solid mesh, shell mesh and hybrid mesh (U900-1 component subjected to three-point bending).
• Figure 10.3.7: Numerical prediction of the cross-section deformation of the U900-1 component subjected to three-point bending using solid modelling, shell modelling and hybrid modelling.
• Figure 10.3.8: Numerical modelling of the axial compression test set-up.
• Figure 10.3.9: Comparison of experimental results and numerical results obtained from solid mesh, shell mesh and hybrid mesh (U900-1 component subjected to axial compression).
• Figure 10.3.10: Numerical prediction of the deformation of the half U900-1 component subjected to axial compression using solid modelling, shell modelling and hybrid modelling at a loading plate displacement of 7.5mm.
• Figure A.1.1: Technical drawing of the three-point bending test set-up for the U900-1 component.
• Figure A.1.2: Technical drawing of the three-point bending test set-up for the U900-1 component: Detail support.
• Figure A.1.3: Technical drawing of the three-point bending test set-up for the U900-1 component: Detail Punch.
• Figure A.2.1: Camera images at first fracture initiation obtained from six parallel three-point bending tests on U900-1 components with focus on gating side and vacuum side: Tests #3 - #5.
• Figure A.2.2: Camera images at first fracture initiation obtained from six parallel three-point bending tests on U900-1 components with focus on gating side and vacuum side: Tests #6 - #8.
• Figure A.2.3: Images of six deformed and fractured U900-1 components subjected to three-point bending.
• Figure A.2.4: Experimental measurements obtained from six parallel three-point bending tests on U900-1 components: Force F1(d1) measured by the testing machine (grey), displacement d1(d1) measured by the testing machine (black), displacement d2(d1) measured by the extensometer at gating side (blue), displacement d3(d1) measured by the extensometer at vacuum side (red), mean dµ23(d1) of both extensometer measurements (green) and gap dδ23(d1) between both extensometer measurements (magenta).
• Figure A.3.1: Technical drawing of the axial compression test set-up for the U900-1 component.
• Figure A.4.1: Images of four deformed and fractured U900-1 components subjected to axial compression.
• Figure A.4.2: Experimental measurements obtained from four parallel axial compression tests on U900-1 components: Force F1(d1) measured by the testing machine (grey), displacement d1(d1) measured by the testing machine (black), displacement d2(d1) measured by the extensometer (blue) and gap dδ12(d1) between both displacement measurements (magenta).
• Figure B.1.1: Uniaxial tensile test specimen UT80 (t = 2.5mm).
• Figure B.1.2: Extraction plan of UT80 specimens machined from U900-1 components.
• Figure B.1.3: Labelling system of UT80 specimens machined from U900-1 components.
• Figure B.2.1: Engineering stress-strain curves obtained from UT80 specimens machined from five U900-1 components presented according to used components.
• Figure B.2.2: Engineering stress-strain curves obtained from UT80 specimens machined from five U900-1 components presented according to extraction positions.
• Figure B.2.3: Correlation matrix of the measured mechanical quantities obtained from UT80 specimens machined from five U900-1 components.
• Figure B.2.4: Averages and COVs of the measured mechanical quantities obtained from UT80 specimens machined from five U900-1 components (Part IF, Part IW and Part BF).
• Figure B.2.5: Average and COVs of the measured mechanical quantities obtained from UT80 specimens machined from five U900-1 components (Part OW and Part OF).
• Figure B.3.1: Uniaxial tensile test specimen UT75 and uniaxial tensile test specimen UT117.
• Figure B.3.2: Extraction plan of UT75 specimens and UT117 specimens machined from U900-1 components.
• Figure B.3.3: Labelling system of UT75 specimens and UT117 specimens machined from U900-1 components.
• Figure B.4.1: Engineering stress-strain curves obtained from UT75 and UT117 specimens machined from six U900-1 components presented according to used components (component #1 - #3).
• Figure B.4.2: Engineering stress-strain curves obtained from UT75 and UT117 specimens machined from six U900-1 components presented according to used components (component #4 - #6).
• Figure B.4.3: Engineering stress-strain curves obtained from UT75 and UT117 specimens machined from six U900-1 components presented according to extraction positions.
• Figure B.4.4: Correlation matrix of the measured mechanical quantities obtained from UT75 specimens machined from six U900-1 components.
• Figure B.4.5: Correlation matrix of the measured mechanical quantities obtained from UT117 specimens machined from six U900-1 components.
• Figure B.4.6: Average and COVs of the measured mechanical quantities obtained from UT75 specimens machined from six U900-1 components.
• Figure B.4.7: Average and COVs of the measured mechanical quantities obtained from UT117 specimens machined from six U900-1 components.
• Figure B.5.1: Average and COVs of the measured thickness obtained from UT80 specimens machined from five U900-1 components.
• Figure B.5.2: Average and COVs of the measured thickness obtained from UT75 and UT117 specimens machined from six U900-1 components.
• Figure C.1.1: Stress update algorithm.
• Figure C.1.2: Element deletion algorithm.
• Figure C.2.1: Material routine MR#1.
• Figure C.3.1: Material routine MR#2.
• Figure C.4.1: Material routine MR#3 (first part).
• Figure C.4.2: Material routine MR#3 (second part).
• Figure C.5.1: Material routine MR#4.

7. 결론:

본 연구는 HPDC 알루미늄 부품의 연성 편차를 전역적 체계적 변화와 국부적 준-무작위적 변화로 성공적으로 분리하여 분석했다. 실험을 통해 주조 시스템이 부품의 거시적 물성 분포에 영향을 미치며, 국부적 편차는 와이블 분포를 따르는 약한 고리(weakest-link) 모델로 설명될 수 있음을 입증했다. 이를 기반으로 개발된 확률론적 고장 모델은 단일 시뮬레이션만으로도 부품의 파괴 확률을 정확하게 예측할 수 있음을 보여주었으며, 이는 기존의 계산 집약적인 몬테카를로 방식에 대한 효율적인 대안을 제시한다. 본 연구는 HPDC 부품의 신뢰성 기반 설계를 위한 견고한 이론적, 실험적 토대를 마련했으며, 향후 주조 공정 시뮬레이션과 연계하여 더욱 정밀한 예측 모델로 발전할 수 있는 가능성을 열었다.

8. 참고 문헌:

• [1] P. Abrahamsen, A Review of Gaussian Random Fields and Correlation Functions, 2nd Ed., Norwegian Computing Center, Oslo, 1997.
• [2] Aleris Switzerland GmbH, Aluminium-Gusslegierungen, Zürich, 2011.
• [3] Altair Engineering Inc: HyperMesh, http://www.altairhyperworks.com/Product,7,HyperMesh.aspx, 2014.
• [4] Aluminium Rheinfelden GmbH, Berichte aus dem Gusswerkstofftechnikum: Nicht alternde Druckgusslegierung für den Automobilbau (Castasil-37 - AlSi9Mn), Rheinfelden, 2004.
• [5] Aluminium Rheinfelden GmbH, Hüttenaluminium Druckgusslegierungen Handbuch 2007, 2nd Ed., Rheinfelden, 2007.
• [6] Aluminium Rheinfelden GmbH, Gießerbrief 27: Highlights der EUROGUSS 2008 von Aluminium Rheinfelden, Rheinfelden, 2008.
• [7] ANSYS Inc: ANSYS, http://www.ansys.com/Products/Simulation+Technology/Structural+Analysis, 2014.
• [8] Y. Bao and T. Wierzbicki, On fracture locus in the equivalent strain and stress triaxiality space, International Journal of Mechanical Sciences 46 (2004), 81 – 98.
• [9] H.J. Bargel and G. Schulze, Werkstoffkunde, 10th Ed., Springer, Berlin, 2009.
• [10] K.J. Bathe, Finite Elemente Methoden, Springer, Berlin, 2001.
• (References continue as listed in the paper)

전문가 Q&A: 자주 묻는 질문

Q1: 확률론적 모델의 파괴 기준으로 Cockcroft-Latham 기준을 선택한 특별한 이유가 있습니까?

A1: Cockcroft-Latham 기준은 연성 파괴를 설명하는 데 널리 사용되는 모델로, 응력과 변형률의 이력을 모두 고려합니다. 특히, 이 기준은 파괴를 단일 임계값인 'Wc'로 정의하기 때문에 와이블 분포와 같은 확률론적 프레임워크 내에서 무작위화(randomize)하기에 매우 적합합니다. 즉, 복잡한 다중 파라미터 모델과 달리 단일 변수(Wc)의 통계적 분포만 정의하면 되므로 모델의 보정과 적용이 상대적으로 용이합니다.

Q2: 논문에서 '결합(Coupled)' 및 '분리(Uncoupled)' 모델링 접근법을 언급했는데, 실용적인 관점에서 어떤 차이가 있습니까?

A2: 이는 매우 중요한 수치 해석적 문제입니다. '결합' 접근법(MR#2)은 무작위 재료 물성 분포를 유한요소(FE) 메쉬 자체에 직접 할당합니다. 이 경우, 해석 정확도를 높이기 위해 메쉬를 더 조밀하게 만들면 재료의 통계적 특성(결함 분포) 자체가 변해버려 메쉬 수렴성 연구가 불가능해집니다. 반면, '분리' 접근법(MR#3, MR#4)은 재료 구조 메쉬(MS Mesh)와 FE 메쉬를 분리하여, FE 메쉬를 변경하더라도 재료의 통계적 특성은 그대로 유지됩니다. 이는 엔지니어가 해석 모델의 신뢰성을 검증하는 데 필수적인 메쉬 수렴성 연구를 가능하게 합니다.

Q3: 이 모델이 기공(porosity)이나 산화막(oxide film)과 같은 특정 유형의 주조 결함을 어떻게 구분하여 고려합니까?

A3: 이 모델은 현상학적(phenomenological) 모델입니다. 즉, 특정 유형의 결함을 개별적으로 모델링하는 대신, 다양한 결함들이 재료의 연성에 미치는 '종합적인 효과'를 통계적으로 포착합니다. SEM 분석을 통해 실제 파단면에서 다양한 결함이 관찰되었으며, 와이블 분포는 이러한 복합적인 불완전성이 최종적으로 재료의 파괴 임계값(Wc)에 미치는 통계적 결과를 효과적으로 모델링합니다.

Q4: 본 연구는 주조 상태(F)의 Castasil-37 합금에 대해 수행되었습니다. 열처리된(예: T7) 합금에도 이 연구 결과를 적용할 수 있습니까?

A4: 논문에서 인용한 다른 연구(Mohr and Treitler [87])에 따르면, 열처리된 합금에서도 상당한 물성 편차가 관찰됩니다. 열처리는 재료를 균질화하고 연성을 향상시키지만, 결함의 근본적인 준-무작위적 특성은 여전히 남아있습니다. 따라서 확률론적 접근법은 열처리 합금에도 매우 유효하며, 다만 해당 재료에 맞게 와이블 분포의 파라미터(형상 계수 m, 척도 계수 Wc0)를 새로 보정하는 과정이 필요합니다.

Q5: 단일 시뮬레이션(MR#1)으로 파괴 확률을 예측하는 것이 완전한 몬테카를로 해석(MR#2)에 비해 갖는 가장 큰 장점은 무엇입니까?

A5: 가장 큰 장점은 압도적인 계산 효율성입니다. 몬테카를로 해석은 통계적 분포를 구축하기 위해 수십, 수백 번의 시뮬레이션을 반복해야 하므로 막대한 시간과 비용이 소요됩니다. 반면, 직접 계산법(MR#1)은 단 한 번의 시뮬레이션으로 동일한 파괴 확률 곡선을 제공하여, HPDC 부품의 설계 및 검증 주기를 획기적으로 단축시킬 수 있습니다.

결론: 더 높은 품질과 생산성을 향한 길

HPDC 부품의 예측 불가능한 연성 편차는 오랫동안 업계의 난제였습니다. 본 연구는 이 문제를 '전역적 체계적 변화'와 '국부적 준-무작위적 변화'로 나누어 접근하는 새로운 패러다임을 제시했습니다. 특히, 확률론적 HPDC 고장 모델링을 통해 단 한 번의 시뮬레이션으로 부품의 파괴 확률을 신뢰성 있게 예측할 수 있음을 입증한 것은 R&D 및 운영 효율성을 극대화할 수 있는 중요한 성과입니다.

CASTMAN은 최신 산업 연구 결과를 적용하여 고객이 더 높은 생산성과 품질을 달성할 수 있도록 최선을 다하고 있습니다. 본 논문에서 논의된 과제가 귀사의 운영 목표와 일치한다면, CASTMAN의 엔지니어링 팀에 연락하여 이러한 원칙을 귀사의 부품에 어떻게 구현할 수 있는지 논의해 보시기 바랍니다.

저작권 정보

• 이 콘텐츠는 "[Octavian Knoll]"의 논문 "[A Probabilistic Approach in Failure Modelling of Aluminium High Pressure Die-Castings]"을 기반으로 한 요약 및 분석 자료입니다.
• 출처: NTNU Open

이 자료는 정보 제공 목적으로만 사용됩니다. 무단 상업적 사용을 금지합니다.
Copyright © 2025 CASTMAN. All rights reserved.