본 논문 소개 내용은 [Int. J. of Applied Mechanics and Engineering, IJME]에 발표된 "[AN OVERVIEW OF HEAT SINK TECHNOLOGY]"의 연구 내용입니다.
1. 개요:
- 제목: 히트싱크 기술 개요 (AN OVERVIEW OF HEAT SINK TECHNOLOGY)
- 저자: Ehsan F. Abbas
- 발행 연도: 2024년
- 발행 저널/학술 학회: 국제 응용 역학 및 공학 저널 (Int. J. of Applied Mechanics and Engineering, IJME)
- 키워드: 열 싱크 설계, 종방향 핀, 열 싱크 성능, 핀 성능 향상, 핀 최적화 (heat sink design, longitudinal fin, performance of a heat sink, improving fin performance, fin optimization)

2. 연구 배경:
- 연구 주제의 사회적/학문적 맥락:
본 연구는 전기 및 전자 장비, 화학 산업, 냉동, 공조 시스템, 발전소 및 기타 열 응용 분야를 포함한 다양한 응용 분야에서 열 에너지를 관리하는 데 있어 열 싱크의 중요한 역할을 다룹니다. 본 논문은 산업 및 가정 환경에서 효율적인 열 관리에 대한 요구 증가에 따라 초기 주철 설계에서 현대적인 솔루션에 이르기까지 열 싱크 기술의 역사적 발전을 강조합니다. 맥락은 진화하는 산업 혁명과 생활 수준 향상을 배경으로 설정되며, 이는 더욱 정교하고 효율적인 열 싱크 설계의 필요성을 주도했습니다. - 기존 연구의 한계:
본 논문은 서론에서 기존 연구의 한계를 명시적으로 자세히 설명하지는 않지만, 특히 종방향 직사각형 핀에 초점을 맞춘 열 싱크 기술에 대한 포괄적인 개요의 필요성을 암묵적으로 제시합니다. 역사적 검토는 열 싱크 기술이 발전해 왔지만, 특히 핀 설계 및 구성과 관련하여 최적의 열 싱크 성능을 달성하는 데 여전히 과제가 남아 있음을 시사합니다. - 연구의 필요성:
본 연구는 특히 강제 및 자연 대류에 노출된 배열에서 종방향 직사각형 핀의 설계 및 최적화에 초점을 맞춰 열 싱크 기술에 대한 구조화된 개요를 제공하기 위해 필요합니다. 본 논문은 다양한 장치의 신뢰성과 성능을 위해 효율적인 열 발산의 중요성을 강조합니다. 역사적 발전, 제조 방법, 냉각 방법, 설계 매개변수 및 최적화 기술을 검토함으로써 본 논문은 지식을 통합하고 해당 분야의 엔지니어와 연구원에게 귀중한 자료를 제공하는 것을 목표로 합니다. 종방향 직사각형 핀에 대한 초점은 일반적인 사용과 최적화를 위한 광범위한 연구 데이터의 가용성으로 정당화됩니다.
3. 연구 목적 및 연구 질문:
- 연구 목적:
본 연구의 주요 목표는 특히 강제 및 자연 대류에 노출된 배열에서 종방향 직사각형 핀의 최적화에 초점을 맞춰 열 싱크 기술에 대한 개요를 제공하는 것입니다. 본 논문은 열 싱크 기술의 발전을 되돌아보고 종방향 직사각형 핀에 대한 기본 원칙과 최적화 기술을 통합하는 것을 목표로 합니다. - 주요 연구 질문:
명시적으로 질문으로 진술되지는 않았지만, 본 연구는 다음과 같은 질문을 암묵적으로 다룹니다.- 열 싱크 기술은 시간이 지남에 따라 어떻게 발전해 왔는가?
- 열 싱크의 다양한 제조 방법과 그 의미는 무엇인가?
- 열 싱크 기술에 사용되는 다양한 냉각 방법은 무엇인가?
- 열 싱크 설계의 주요 설계 매개변수 및 가정은 무엇인가?
- 특히 종방향 직사각형 핀에 대한 열 싱크 설계 및 최적화에 대한 이론적 접근 방식은 무엇인가?
- 핀 효율성 및 유효성은 어떻게 평가하고 최적화할 수 있는가?
- 다양한 조건에서 다양한 핀 프로파일에 대한 최적 치수는 무엇인가?
- 다중 핀 배열의 열 저항은 어떻게 분석할 수 있는가?
- 열 싱크 성능에 대한 실험적 및 수치적 연구 결과는 무엇인가?
- 연구 가설:
본 논문은 개요이며 특정 가설을 검증하지 않습니다. 그러나 기존 문헌에 대한 포괄적인 검토가 열 싱크, 특히 종방향 직사각형 핀의 설계 및 최적화에 대한 귀중한 통찰력과 지침을 제공할 수 있다는 암묵적 가정을 기반으로 합니다. 본 논문은 해당 분야에 대한 구조화된 이해를 제시하기 위해 기존 지식을 종합합니다.
4. 연구 방법론
- 연구 설계:
문헌 검토. 본 논문은 열 싱크 기술, 특히 종방향 직사각형 핀에 초점을 맞춰 기존 연구 및 지식을 종합하는 검토 논문입니다. - 자료 수집 방법:
자료 수집 방법은 열 싱크 기술과 관련된 연구 논문, 서적 및 기술 보고서를 포함한 출판된 문헌에 대한 포괄적인 검토를 포함합니다. 논문 말미에 나열된 참고 문헌은 정보 출처를 나타냅니다. - 분석 방법:
분석 방법은 질적이며 검토된 문헌에서 정보를 요약, 종합 및 구성하는 것을 포함합니다. 본 논문은 역사적 발전, 제조 방법, 냉각 방법, 설계 매개변수, 이론적 모델, 최적화 기술 및 실험적/수치적 결과를 포함하여 열 싱크 기술의 다양한 측면에 대한 구조화된 개요를 제시합니다. 인용된 연구의 수학 방정식과 그림은 주요 개념과 결과를 설명하는 데 사용됩니다. - 연구 대상 및 범위:
연구 주제는 열 싱크 기술이며, 특히 종방향 직사각형 핀에 초점을 맞춥니다. 검토는 열 싱크 설계, 최적화 및 성능 평가의 다양한 측면을 다루며, 해당 분야의 광범위한 연구를 활용합니다. 범위는 주로 열 싱크, 특히 종방향 직사각형 핀 구성의 열 전달과 관련된 이론적 및 실험적 연구에 초점을 맞춥니다.
5. 주요 연구 결과:
- 주요 연구 결과:
- 역사적 발전: 본 논문은 20세기 초의 다중 컬럼 주철 설계에서 현대적인 재료 및 제조 기술에 이르기까지 열 싱크의 진화를 추적하고 사회적 및 산업적 변화에 의해 주도된 주요 이정표와 설계 우선 순위의 변화를 강조합니다.
- 제조 방법: 본 검토는 스탬핑, 압출, 접착 핀, 주조 및 용접 핀을 포함한 열 싱크의 다양한 제조 방법을 개략적으로 설명하고 각 방법의 장점, 한계 및 응용 분야를 자세히 설명합니다. 그림 1은 제조 방법에 따른 열 싱크 샘플의 그림을 보여줍니다.
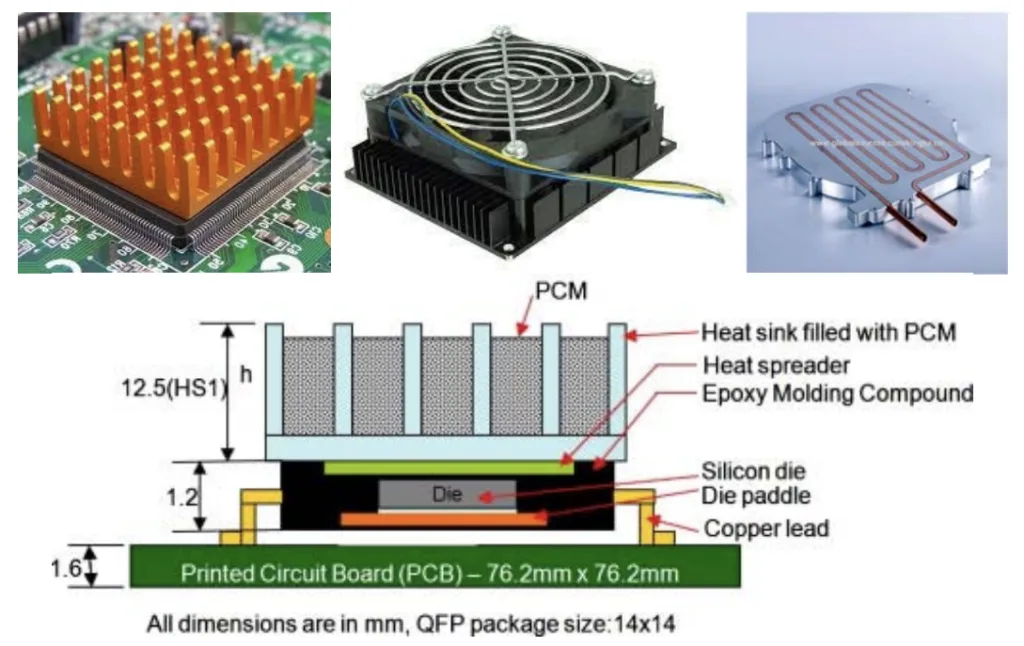
- 냉각 방법: 본 논문은 냉각 방법을 수동, 능동, 준능동, 액체 냉각 플레이트 및 상변화 재순환 시스템으로 분류하고 각 방법의 작동 원리 및 일반적인 응용 분야를 설명합니다. 그림 2는 냉각 방법에 따른 열 싱크 샘플의 그림을 보여줍니다.
- 설계 매개변수 및 가정: 유속, 압력 강하, 단면적, 열 전달 요구 사항, 작동 온도, 크기 제한, 중력 방향, 외관 및 비용을 포함한 열 싱크의 주요 설계 매개변수가 식별됩니다. 단순화된 분석을 위해 열 싱크 설계에서 이루어진 가정(예: 무시할 수 있는 복사열 전달 및 균일한 베이스 온도)도 나열됩니다.
- 설계에 대한 이론적 접근: 본 논문은 종방향 직사각형 핀에 초점을 맞춰 열 싱크 설계를 위한 이론적 프레임워크를 제시합니다. 온도 분포 방정식(그림 3), 다양한 핀 팁 조건에 대한 열 전달 방정식(표 1 및 2), 핀 효율성 및 유효성에 대한 방정식을 제공합니다.
- 핀 최적화: 본 검토에서는 수정된 프로파일 길이, 핀 유효성 및 일정한 열 유속 및 일정한 부피 조건에서 핀 두께 및 길이를 최적화하는 방법을 포함한 핀 최적화 기술에 대해 논의합니다. 최적 핀 치수에 대한 방정식이 제시됩니다.
- 다중 핀 배열의 열 저항: 본 논문은 다중 핀 배열의 열 저항을 분석하고 열 전달률 및 전체 표면 효율성을 계산하기 위한 공식을 제공합니다(그림 4).
- 불균일 프로파일 면적을 가진 종방향 핀: 검토는 불균일 프로파일(삼각형, 오목, 볼록)을 가진 종방향 핀으로 확장되어 이러한 핀 모양에 대한 최적 치수 방정식과 열 전달 방정식을 제시합니다(그림 5 및 표 3).
- 종방향 핀 배열: 본 논문은 자연 층류 대류를 위한 핀 배열에서 평행 수직판 사이의 간격 최적화에 대해 논의하고 열 전달률 및 배열 설계를 위한 최적 매개변수에 대한 방정식을 제시합니다(그림 6 및 7).
- 실험적 및 수치적 연구: 본 검토는 핀 형상, 간격, 방향 및 유동 조건의 영향을 포함하여 열 싱크 성능의 다양한 측면을 조사한 수많은 실험적 및 수치적 연구 결과를 요약합니다. 그림 8은 기존 및 하이브리드 열 싱크 모델을 보여주고, 그림 9는 연구된 열 싱크 모델을 보여줍니다.
- 통계적/질적 분석 결과:
본 논문은 주로 다양한 연구에서 질적 결과를 종합합니다. 정량적 결과는 열 전달률, 핀 효율성, 최적 치수 및 열 저항에 대한 방정식 및 공식 형태로 제시됩니다. 검토에서는 핀 간격이 열 전달 계수에 미치는 영향, 인터럽트 핀의 효과, 다양한 핀 모양의 성능과 같은 실험적 및 수치적 연구의 추세와 일반적인 결론을 강조합니다. - 데이터 해석:
본 논문에 제시되고 종합된 데이터는 열 싱크, 특히 종방향 직사각형 핀의 설계 및 최적화가 수많은 매개변수와 고려 사항을 포함하는 복잡한 프로세스임을 나타냅니다. 최적 설계는 응용 분야, 냉각 방법, 재료 속성 및 환경 조건을 포함한 다양한 요인에 따라 달라집니다. 검토에서는 효율적인 열 싱크 설계를 달성하는 데 있어 이론적 모델링, 수치 시뮬레이션 및 실험적 검증의 중요성을 강조합니다. - 그림 목록:
- 그림 1. 제조 방법에 따른 열 싱크 샘플 그림.
- 그림 2. 냉각 방법에 따른 열 싱크 샘플 그림.
- 그림 3. 직사각형 단면을 가진 종방향 핀 [8].
- 그림 4. 평면 벽과 핀의 조합에서 열 손실 스케치.
- 그림 5. 불균일 프로파일 면적을 가진 종방향 핀 스케치: (a) 삼각형, (b) 오목, (c) 볼록 [9].
- 그림 6. 종방향 핀 배열 및 기하학적 정의 스케치 [9], [18].
- 그림 7. 종방향 핀 배열에 대한 최적 β 값 [9, 18].
- 그림 8. 두 가지 열 싱크 모델 스케치: (a) 기존, (b) 하이브리드.
- 그림 9. 연구된 열 싱크 모델 스케치, (a) 직선 핀, (b) 토폴로지.

6. 결론 및 논의:
- 주요 결과 요약:
본 개요 논문은 직사각형 종방향 핀을 가진 열 싱크의 설계 최적화가 지난 세기에 걸쳐 광범위하게 연구되었다고 결론 내립니다. 최적 구성을 결정하기 위해 다양한 실험적, 수치적 및 이론적 방법이 사용되었습니다. 주요 결과는 핀 높이와 간격이 열 전달률에 상당한 영향을 미치며, 최적 핀 간격이 열 전달을 최대화하는 데 중요하다는 것을 나타냅니다. 듀랄루민 핀은 유사한 형상에서 스테인리스강보다 성능이 뛰어납니다. 인터럽트 및 경사 핀, 그리고 직사각형 노치 핀과 같은 특정 핀 형상은 열 전달 성능을 향상시킬 수 있습니다. - 연구의 학문적 의의:
본 검토 논문은 열 싱크 기술, 특히 종방향 직사각형 핀에 대한 광범위한 연구 결과를 통합하여 귀중한 학문적 기여를 제공합니다. 역사적 발전, 설계 원칙, 최적화 기술 및 실험 결과에 대한 구조화된 개요를 제공하여 열 공학 연구자 및 학생들에게 포괄적인 자료 역할을 합니다. 본 논문은 열 싱크 설계의 발전과 성능에 영향을 미치는 주요 요인을 강조합니다. - 실용적 의미:
본 연구의 실용적 의미는 다양한 산업 분야의 열 관리에 관련된 엔지니어 및 설계자에게 중요합니다. 본 논문은 다양한 응용 분야 및 냉각 조건에 맞는 열 싱크를 설계하고 최적화하기 위한 지침과 방정식을 제공합니다. 요약된 결과는 전자 장치, 전력 시스템 및 기타 열 응용 분야에서 효율적이고 비용 효율적인 열 발산을 달성하기 위해 적절한 제조 방법, 냉각 전략, 핀 형상 및 재료를 선택하는 데 도움이 될 수 있습니다. 최적 핀 간격에 대한 강조와 인터럽트 및 경사 핀의 성능 이점은 실용적인 설계 개선을 위한 실행 가능한 통찰력을 제공합니다. - 연구의 한계:
검토 논문으로서 한계는 검토된 문헌의 범위에 내재되어 있습니다. 본 논문은 광범위한 개요를 제공하지만 열 싱크 기술의 모든 단일 연구 또는 측면을 철저히 다루지는 않을 수 있습니다. 초점은 주로 종방향 직사각형 핀에 있으며, 다른 핀 구성 또는 고급 열 싱크 기술은 덜 광범위하게 다루어질 수 있습니다. 검토는 또한 포함된 연구 선택에 의해 제한되며, 일반적으로 연구되는 영역에 대한 편견을 반영할 수 있습니다.
7. 향후 후속 연구:
- 후속 연구 방향:
본 논문은 향후 연구를 위한 여러 방향을 암묵적으로 제시합니다.- 기존 설계를 뛰어넘어 열 전달 성능을 향상시키기 위한 고급 열 싱크 형상 및 재료에 대한 추가 연구.
- 복잡하고 최적화된 핀 구조의 생산을 가능하게 하는 새로운 제조 기술 탐색.
- 향상된 효율성과 적응성을 위해 수동 및 능동 냉각 전략을 결합한 하이브리드 냉각 방법에 대한 추가 연구.
- 실제 작동 조건에서 최적화된 열 싱크의 장기적인 신뢰성 및 성능에 대한 심층 연구.
- 고전력 밀도 전자 장치 및 지속 가능한 에너지 시스템과 같이 특정 열 관리 과제가 있는 새로운 응용 분야를 위한 열 싱크 설계 조사.
- 특히 복잡한 핀 형상 및 유동 조건에서 보다 포괄적인 실험 데이터로 기존 이론적 모델 및 수치 시뮬레이션을 개선하고 검증하기 위한 추가 연구.
- 추가 탐색이 필요한 영역:
- 공간 제약, 무게 제한 및 비용 효율성과 같은 요소를 고려하여 특정 응용 분야 및 환경 조건에 맞는 열 싱크 최적화.
- 복잡한 유동 체제에서 열 싱크 성능을 예측하기 위한 보다 정확하고 계산적으로 효율적인 수치 모델 개발.
- 제조 공차 및 표면 마감이 열 싱크의 실제 열 성능에 미치는 영향 조사.
- 전체적인 열 솔루션을 위해 시스템 수준의 열 관리 전략과 통합되는 혁신적인 열 싱크 설계 탐색.
8. 참고 문헌:
- [1] Kordyban T. (1998): Hot Air Rises and Heat Sinks: Everything You Know About Cooling Electronics Is Wrong.- ASME Press, p.236, https://doi.org/10.1115/1.800741.
- [2] Lee S. (1995): Optimum design and selection of heat sinks.– IEEE Transactions on Components, Packaging, and Manufacturing Technology: Part A, vol.18, No.4, pp. 812-817, doi: 10.1109/95.477468.
- [3] Londhe K. and Kaushik V.R. (2017): Heat sink design for optimal performance of compact electronic appliances - a review.- Journal for Advanced Research in Applied Sciences, vol.4, No.5, pp.13-21.
- [4] Kandasamy R., Wang X.Q. and Mujumdar A.S. (2008): Transient cooling of electronics using phase change material (PCM)-based heat sinks.- Appl. Therm. Eng., vol.28, No.8-9, pp.1047-1057, doi: 10.1016/J.APPLTHERMALENG.2007.06.010.
- [5] Kays W.M. and London A.L. (2011): Compact Heat Exchangers.– Third Edition,
- [6] https://celsiainc.com/technology/heat-sink-design/.
- [7] Lee H.S. (2010): Thermal Design: Heat Sinks, Thermoelectrics, Heat Pipes, Compact Heat Exchangers, and Solar Cells.- John Wiley & Sons, Inc., doi: 10.1002/9780470949979.
- [8] Holman J.P. (2010): Heat Transfer.– 10th ed., p.758, McGraw-Hill Education
- [9] Kraus A.D., Aziz A. and Welty J. (2001): Extended Surface Heat Transfer.– A Wiley-Interscience Publication J.WILEY & SONS, Inc., doi: 10.1002/9780470172582.
- [10] Cengel Y., Turner R. and Smith R. (2001): Fundamentals of thermal-fluid sciences.- Appl. Mech. Rev., vol.54, No.6, doi: 10.1115/1.1421126.
- [11] Brown A. (1965): Optimum dimensions of uniform annular fins.– Int. J. Heat Mass Transf., vol.8, No.4, pp.655-662, doi: 10.1016/0017-9310(65)90051-7.
- [12] Cobble M.H. (1971): Optimum fin shape.- J. Franklin Inst., vol.291, No.4, pp.283-292, doi: 10.1016/0016-0032(71)90184-0.
- [13] Snider A.D. and Kraus A.D. (1987): The quest for the optimum longitudinal fin profile.– Heat Transfer Engineering, vol.8, No.2, doi: 10.1080/01457638708962790.
- [14] Duffin R. (1959): A variational problem relating to cooling fins.- Indiana University Mathematics Journal, vol.8, No.1, doi: 10.1512/iumj.1959.8.58003.
- [15] Maday C.J. (1974): The minimum weight one-dimensional straight cooling fin.– J. Eng. Ind., vol.96, No.1, pp.161-165, https://doi.org/10.1115/1.3438291 .
- [16] Ernst E.R.G., Eckert R.G. and Drake R.M. (1987): Analysis of heat and mass transfer.- Hemisphere Pub. Corp., accessed: Nov. 21, 2023, [Online], available: https://inis.iaea.org/search/search.aspx?orig_q=RN:19100674
- [17] Razelos P. and Imre K. (1983): Minimum mass convective fins with variable heat transfer coefficients.- J. Franklin Inst., vol.315, No.4, doi: 10.1016/0016-0032(83)90078-9.
- [18] Aziz A. (1992): Optimum dimensions of extended surfaces operating in a convective environment.– Appl. Mech. Rev., vol.45, No.5, doi: 10.1115/1.3119754.
- [19] Bergman T.L., Lavine A.S., Incropera F.P. and DeWitt D.P. (2015): Fundamentals of Heat and Mass Transfer.- John Wiley & Sons, USA.
- [20] Chung B.T.F. and Iyer J.R. (1993): Optimum design of longitudinal rectangular fins and cylindrical spines with variable heat transfer coefficient.- Heat Transfer Engineering, vol.14, No.1, pp.31-41, doi: 10.1080/01457639308939792.
- [21] Schmidt E. (1926): Die Wärmeübertragung Durch Rippen.
- [22] Chung B.T.F. and Nguyen L.D. (1986): Optimization of design parameters for radiating longitudinal fins of various geometries.- in AIAA Paper, doi: 10.2514/6.1986-150.
- [23] Levy E.K. (1971): Optimum plate spacings for laminar natural convection heat transfer from parallel vertical isothermal flat plates.– J. Heat Transfer, vol.93, No.4, pp.463-465, doi: 10.1115/1.3449847.
- [24] Elenbaas W. (1942): Heat dissipation of parallel plates by free convection.- Physica, vol.9, No.1, pp.1-28, doi: 10.1016/S0031-8914(42)90053-3.
- [25] Bodoia J.R. and Osterle J.F. (1962): The development of free convection between heated vertical plates.- J. Heat Transfer, vol.84, No.1, pp.40-43, doi: 10.1115/1.3684288.
- [26] Bar-Cohen A. and Jelinek M. (1985): Optimum arrays of longitudinal, rectangular fins in corrective heat transfer.- Heat Transfer Engineering, vol.6, No.3, pp.68-78, doi: 10.1080/01457638508939633.
- [27] Starner K.E. and McManus H.N. (1963): An experimental investigation of free-convection heat transfer from rectangular-fin arrays.- J. Heat Transfer, vol.85, No.3, pp.273-277, doi: 10.1115/1.3686097.
- [28] Jones C.D. and Smith L.F. (1970): Optimum arrangement of rectangular fins on horizontal surfaces for free-convection heat transfer.- J. Heat Transfer, vol.92, No.1, doi: 10.1115/1.3449648.
- [29] Barrett A.V. and Obinelo I.F. (1997): Characterization of longitudinal fin heat sink thermal performance and flow bypass effects through CFD methods.- in Annual IEEE Semiconductor Thermal Measurement and Management Symposium, doi: 10.1109/stherm.1997.566793.
- [30] De Lieto Vollaro A., Grignaffini S. and Gugliermetti F. (1999): Optimum design of vertical rectangular fin arrays.- International Journal of Thermal Sciences, vol.38, No.6, pp. 525-529, doi: 10.1016/S1290-0729(99)80025-8.
- [31] Baskaya S., Sivrioglu M. and Ozek M. (2000): Parametric study of natural convection heat transfer from horizontal rectangular fin arrays.– International Journal of Thermal Sciences, vol.39, No.8, pp.797-805, doi: 10.1016/S1290-0729(00)00271-4.
- [32] Bar-Cohen A., Iyengar M. and Kraus A.D. (2003): Design of optimum plate-fin natural convective heat sinks.- Journal of Electronic Packaging, Transactions of the ASME, vol.125, No.2, pp.208-216, SPEC., doi: 10.1115/1.1568361.
- [33] Yazicioğlu B. and Yüncü H. (2007): Optimum fin spacing of rectangular fins on a vertical base in free convection heat transfer.- Heat and Mass Transfer/Waerme- und Stoffuebertragung, vol.44, No.1, pp.11-21, doi: 10.1007/s00231-006-0207-6.
- [34] Mittelman G., Dayan A., Dado-Turjeman K. and Ullmann A. (2007): Laminar free convection underneath a downward facing inclined hot fin array.- Int. J. Heat Mass Transf., vol.50, No.13-14, pp.2582-2589, doi: 10.1016/j.ijheatmasstransfer.2006.11.033.
- [35] Shaeri M.R. and Yaghoubi M. (2009): Thermal enhancement from heat sinks by using perforated fins.– Energy Convers. Manag., vol.50, No.5, pp.1264-1270, doi: 10.1016/j.enconman.2009.01.021.
- [36] Kim D.K. (2012): Thermal optimization of plate-fin heat sinks with fins of variable thickness under natural convection.- Int. J. Heat Mass Transf., vol.55, No.4, pp.752-761, doi: 10.1016/j.ijheatmasstransfer.2011.10.034.
- [37] Ahmadi M., Mostafavi G. and Bahrami M. (2014): Natural convection from rectangular interrupted fins.- International Journal of Thermal Sciences, vol.82, No.1, pp.62-71, doi: 10.1016/j.ijthermalsci.2014.03.016.
- [38] Pouryoussefi S. and Zhang Y. (2015): Experimental study of air-cooled parallel plate fin heat sinks with and without circular pin fins between the plate fins.- Journal of Applied Fluid Mechanics, vol.8, No.3, pp.515-520, doi: 10.18869/acadpub.jafm.67.222.22930.
- [39] Karamanis G. and Hodes M. (2016): Longitudinal-fin heat sink optimization capturing conjugate effects under fully developed conditions.– J. Therm. Sci. Eng. Appl., vol.8, No.4, p.7, doi: 10.1115/1.4034339.
- [40] Shadlaghani A., Tavakoli M.R., Farzaneh M. and Salimpour M.R. (2016): Optimization of triangular fins with/without longitudinal perforate for thermal performance enhancement.– Journal of Mechanical Science and Technology, vol.30, No.4, pp.1903-1910, doi: 10.1007/s12206-016-0349-5.
- [41] Hong S.H. and Chung B.J. (2016): Variations of the optimal fin spacing according to Prandtl number in natural convection.- International Journal of Thermal Sciences, vol.101, pp.1-8, doi: 10.1016/J.IJTHERMALSCI.2015.10.026.
- [42] Dogan M. and Dogan D. (2017): Experimental investigation of natural convection heat transfer from fin arrays for different tip-to-base fin spacing ratios.- Isi Bilimi Ve Teknigi Dergisi/ Journal of Thermal Science and Technology, vol.37, No.1, pp.147-157.
- [43] Jaya Krishna D. (2018): Operational time and melt fraction based optimization of a phase change material longitudinal fin heat sink.– J. Therm. Sci. Eng. Appl., vol.10, No.6, p.4, doi: 10.1115/1.4040988.
- [44] Hou D., Xin X. and Qian J. (2020): Analysis of natural convection heat transfer from vertical and inclined plate fin heat sinks.- in Lecture Notes in Electrical Engineering, Springer Verlag, pp.479-487, doi: 10.1007/978-981-32-9441-7_49.
- [45] Jasim H.H. (2020): Heat transfer enhancement from heat sources using optimal design of combined fins heat-sinks.- Propulsion and Power Research, vol.9, No.4, pp.372-382, doi: 10.1016/j.jppr.2020.11.002.
- [46] Xie L., Zhang Y., Ge M. and Zhao Y. (2022): Topology optimization of heat sink based on variable density method.– Energy Reports, vol.8, pp.718-726, doi: 10.1016/J.EGYR.2021.11.214.
- [47] Obaid A.J. and Hameed V.M. (2023): An experimental and numerical comparison study on a heat sink thermal performance with new fin configuration under mixed convective conditions.– S. Afr. J. Chem. Eng., vol.44, pp.81-88, doi: 10.1016/J.SAJCE.2023.01.009.
- [48] Kaya M. and Kaya Ş. (2023): Optimum fin spacing of rectangular fins on aluminum heat sinks plates.- Proceedings of the Romanian Academy Series A - Mathematics Physics Technical Sciences Information Science, vol.24, No.2, pp.157-157.
9. 저작권:
- 본 자료는 "[Ehsan F. Abbas]"의 논문: "[열 싱크 기술 개요 (AN OVERVIEW OF HEAT SINK TECHNOLOGY)]"를 기반으로 합니다.
- 논문 출처: https://doi.org/10.59441/ijame/192127
본 자료는 상기 논문을 기반으로 요약되었으며, 상업적 목적으로 무단 사용하는 것을 금지합니다.
Copyright © 2025 CASTMAN. All rights reserved.