高出力密度アプリケーション向けアウターローター型誘導電動機の熱モデルのパラメータ化

この入門論文の内容は、Przegląd Elektrotechnicznyによって発行された論文「Parametrization of the thermal model of induction motor with outer rotor」に基づいています。

1. 概要:

• タイトル: アウターローター型誘導電動機の熱モデルのパラメータ化
• 著者: Szczepan Opach, Tomasz Wolnik
• 出版年: 2023年
• 出版ジャーナル・学会: Przegląd Elektrotechniczny
• キーワード: CFDシミュレーション、熱モデル、誘導電動機、高出力密度電動機

2. アブストラクト:

本論文では、高出力密度のアウターローター型誘導電動機を例として、電動機の熱モデルのパラメータ化手法を提示する。本論文で提示するシミュレーションは、定格出力25kW、質量16kgの銅製かご形回転子を備えた電動機モデルを用いて実施した。この構造は、さらされる運転条件が厳しいため、設計段階で正確な熱解析が必要となる。多くの研究では、この解析は通常、電動機の回転要素を考慮しない熱シミュレーションに限定されている。本稿では、回転子の回転運動、ローター本体の外面と環境との間の対流熱交換の強度を記述する対流係数、および固定子巻線熱伝導率の代替数値決定法を考慮して、エアギャップを通る熱伝達係数の値を含む、CFDモデルの選択されたパラメータの数値的決定法を提示する。数値シミュレーションで得られた結果に基づいて、電動機の3次元CFDモデルを開発し、解析した。

3. 導入:

近年における方向性の一つは、希土類永久磁石に依存しない高効率電気駆動装置の開発である[1-5]。これは、いわゆる比出力[kW/kg]、つまり与えられた機械の出力密度を知らせる駆動装置にも当てはまる[1,4,6]。さらに、近年、電気機械に対する騒音低減、信頼性、そして最終的には材料と製造コストの要求の高まりは、その設計の最適化を迫っている[7-8]。もちろん、技術と運転パラメータの点では、永久磁石を備えたモーターは基本的に競争相手がおらず、最高の特性を備えている。しかし、主要部品の多様化やグローバルな独占からの独立など、重要な問題の全スペクトルを考慮すると、誘導電動機を含む他のタイプの機械の開発と改良への関心が再び高まっている。モーターの設計段階における重要な課題は、モーターの適切な熱モデルと熱シミュレーション[6,9,10]である。高出力密度モーターは、多くの場合[12-15 A/mm²]の高電流負荷および高電源電圧周波数[800-1000 Hz]の条件下で動作するため、これらの機械の機械構造の部品は、負の熱影響[11-12]に特にさらされる。これらには、巻線、軸受、永久磁石、シャフトシール、エンコーダ[9]が含まれる。電気機械の熱状態の影響は、部品の嵌め合い、組立隙間、または接続の設計を選択する際にも考慮する必要がある。電気機械の熱状態が効率に与える影響も大きい[9,13]。

現在、多くの科学的研究で、電気自動車分野（自動車、航空、海運）[6,14,15]向けの電気機械の熱計算に注意が払われている。さらに、熱計算の問題は、比出力の高いモーターを設計する場合に特に重要である。これらの計算では、CFD熱流体シミュレーションを使用して、任意の動作点（例えば、定格または過負荷）で負荷をかけられた電気機械の定常状態熱状態を決定する。CFD計算はまた、冷却システムの効率を最適化することにより、電気機械からの熱除去を強化することを可能にする。

3次元CDFモデルは、以前に準備され、適切に簡略化された3次元CADモデルと、使用される構造材料の特性に基づいて開発される。これには以下が含まれる。

• 材料の熱伝導率 λ (W/mK)
• 材料の比熱 Cp (J/kgK)
• 材料密度 ρ (kg/m³)
• 液体の動粘度 η (kg/ms)
• 液体の動粘度 ν (m²/s)

さらに、CFDモデルは、タスクのいわゆる境界条件を考慮して準備される。境界条件には、以下のようなものがある。

• 周囲温度 Ta (°C)
• 単位時間あたりの冷却材流量 F (kg/s)
• 冷却システムの入口における温度 Tin (°C) または流体圧力 Pin (bar)
• 自然対流係数 an (W/m²K) および強制対流係数 af (W/m²K)
• モデルの熱バリアを通る熱伝達係数 k (W/m²K) またはそれらの逆数である熱バリアの熱抵抗 Rt (m²K/W)

モデルの熱負荷、すなわち電力損失 ΔP (W) の値は、単位時間あたりに電気機械の個々の部品で生成される熱エネルギーの量を表す。最も一般的な値は、以下の電力損失である。

• 固定子巻線 ΔPcus (W)
• 固定子コア ΔPFes (W)
• 回転子巻線 ΔPcur (W)
• 回転子コア ΔPFer (W)
• 軸受における機械的損失 ΔPb

4. 研究の概要:

研究テーマの背景:

高出力密度電動機、特に誘導電動機は、特に電動モビリティにおいてますます重要になっている。これらのモーターは、信頼性と効率を確保するために正確な熱管理を必要とする厳しい条件下で動作する。正確な熱解析は、設計段階で不可欠である。

先行研究の状況:

従来の熱解析では、回転部品を無視し、対流係数に一定の値を用いることでモデルを簡略化することが多かった。CFDモデルにおけるエアギャップのメッシュ分割も、モーター全体の寸法に比べて寸法が小さいため、メッシュ品質の問題（アスペクト比）を引き起こし、課題となっている。

研究の目的:

本研究は、高出力密度のアウターローター型誘導電動機のパラメータ化された熱モデルを開発することを目的としており、CFDモデリングのための主要なパラメータの数値的決定に焦点を当てている。これには以下が含まれる。

• 回転子の動きを考慮したエアギャップを通る熱伝達係数 kag (W/m²K)。
• アウターローター表面の対流係数 af (W/m²K)。
• 固定子巻線の代替熱伝導率係数 Axy、Az (W/mK)。

コアとなる研究:

本研究は、8000rpmで動作する25kW、16kgの銅製かご形アウターローター型誘導電動機の3D CFD熱モデルのパラメータを数値的に決定することに焦点を当てている。目的は、モーター部品の定常状態温度を正確に予測し、冷却材の除熱効率を分析することである。

5. 研究方法

研究デザイン:

本研究では、数値流体力学（CFD）ソフトウェアANSYS 2021 R2 Fluentを用いた数値シミュレーションを採用している。熱モデルのパラメータ化は、重要な熱伝達パラメータを決定するための専用の数値実験のシリーズを通して達成された。

データ収集と分析方法:

• エアギャップを通る熱伝達係数 (kag): 3Dエアギャップモデルを作成し、ANSYS Fluentでシミュレーションを行い、回転子の回転を考慮してエアギャップの等価熱抵抗 Rtag (m²K/W) を数値的に決定した。温度 T1 と T2 を円筒面に割り当て、熱流束 q (W) を計算して、式 (2) を用いて kag と Rtag を導き出した。
• アウターローター表面の強制対流係数 (af): ローターと周囲の空気の2Dモデルをシミュレーションした。様々な温度差 ΔT と回転速度に対する数値シミュレーションを実施し、単位熱流束 ġ (W/m²) を決定し、続いて式 (3) を用いて af を計算した。
• スロット断面における固定子巻線の等価熱伝導率係数 (Axy): 「正方形」および「三角形」構成で配置された巻線ワイヤを備えた固定子スロットの2Dモデルをシミュレーションした。与えられた温度差 ΔT に対する熱流束 q (W) を計算して、式 (1) を用いて代替熱伝導率係数 Axy を決定した。

研究テーマと範囲:

本研究は、高出力密度アプリケーション向けに設計された銅製かご形アウターローター型誘導電動機に焦点を当てている。範囲は以下を含む。

• 回転子の回転を考慮したエアギャップ熱伝達係数の数値的決定。
• アウターローター表面の強制対流係数の数値的決定。
• 固定子巻線の等価熱伝導率の数値的決定。
• モーターの3D CFD熱モデルの開発と解析。
• 定常状態温度分布と冷却材除熱の解析。

6. 主要な結果:

主要な結果:

• エアギャップを通る熱伝達係数 kag は、回転子の動きを考慮して数値的に決定され、エアギャップの等価熱抵抗は Rtag = 0.00773 m²K/W であることが判明した。
• アウターローター本体の外面の強制対流係数 af は、回転速度 8000 rpm で 58.43 W/m²K、4000 rpm で 32.76 W/m²K と数値的に決定された。
• スロット断面における固定子巻線の等価熱伝導率係数 Axy は、「正方形」構成で含浸ワニス充填の場合、1.39 W/mK であると決定された。
• これらの数値的に導出された係数と熱抵抗（表11）でパラメータ化された3D CFDモデルを解析し、モーターの定常状態熱挙動を予測した（図11〜17）。
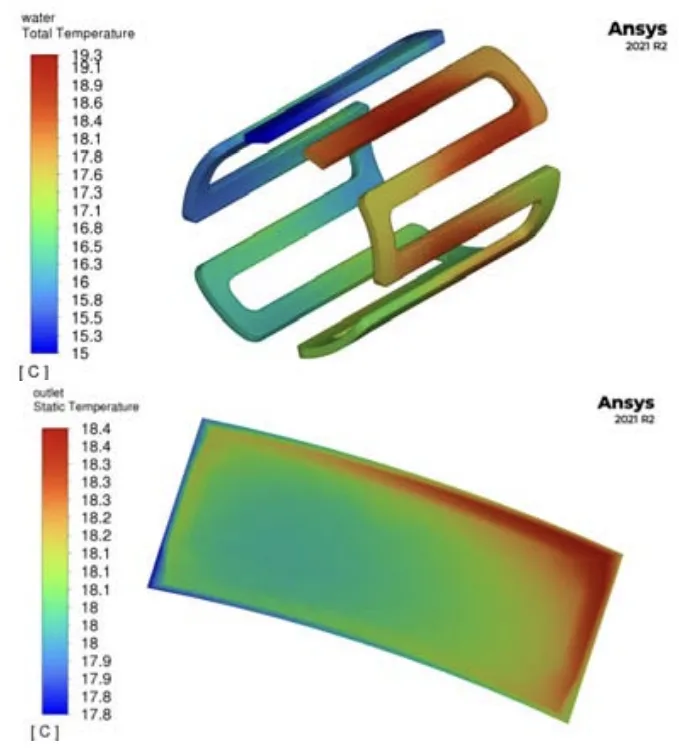
• 冷却材（水）の温度上昇は ΔT = 3.1 °C と計算され、冷却システムによる効率的な除熱を示している。

図のリスト:

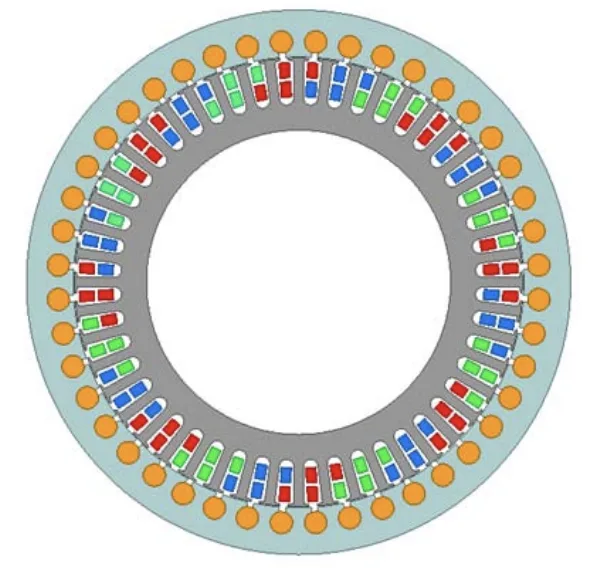
• Fig. 1. 電磁回路モデルのアウターローター型誘導電動機。
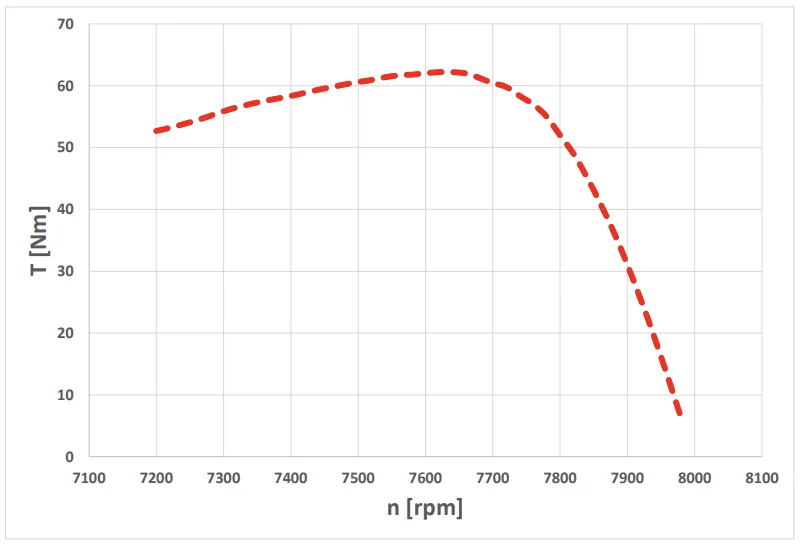
• Fig. 2. 回転速度特性に対するトルク。
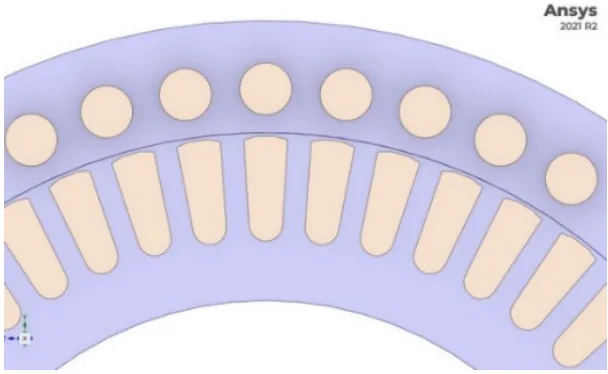
• Fig. 3. アウターローター型誘導電動機のCADモデル
• Fig. 4. ANSYSソフトウェアにおける有限要素メッシュを備えたモーターモデル
• Fig. 5. ANSYSソフトウェアにおける有限要素メッシュを備えた冷却材
• Fig. 6. エアギャップを省略した誘導電動機の固定子と回転子の簡略化モデル
• Fig. 7. ANSYSにおける有限要素メッシュを備えたエアギャップの3Dモデル
• Fig. 8. 回転数 n = 8000 rpm におけるローター周辺の温度分布。
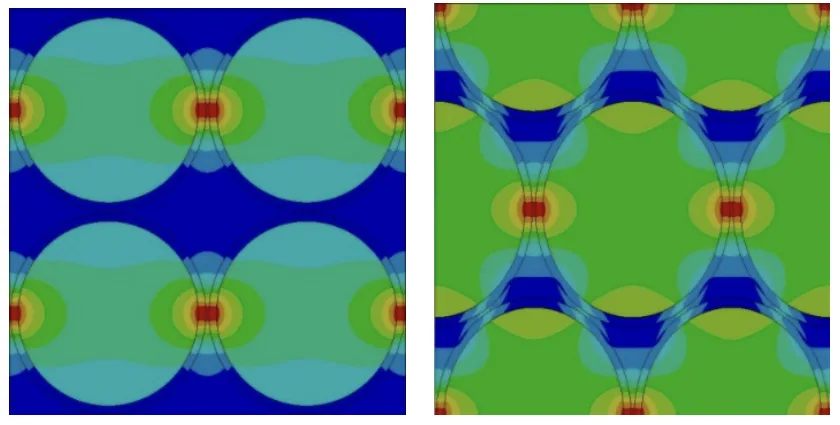
• Fig. 9. スロットを充填した「正方形」および「三角形」構成の試験サンプルにおける温度分布（含浸ワニス充填）。
• Fig. 10. スロットを充填した「正方形」および「三角形」構成の試験サンプルにおける温度分布（空気充填）。
• Fig. 11. 巻線と固定子コアにおける計算された熱定常状態
• Fig. 12. 銅製かご形回転子における計算された熱定常状態
• Fig. 13. 回転子コアにおける計算された熱定常状態
• Fig. 14. 回転子ハウジングにおける計算された熱定常状態
• Fig. 15. 固定子ハウジングにおける計算された熱定常状態
• Fig. 16. シャフトと軸受における計算された熱定常状態
• Fig. 17. 冷却材（水）の計算された熱定常状態

7. 結論:

本研究では、高出力密度のアウターローター型誘導電動機の熱モデルをパラメータ化する手法を提示した。数値的手法を用いて、エアギャップを通る熱伝達係数、アウターローター表面の対流係数、固定子巻線の等価熱伝導率などの重要なパラメータを決定した。これらのパラメータをその後、3D CFDモデルの開発と解析に利用し、モーターの熱挙動を正確に予測することを可能にした。結果は、高出力密度モーターの詳細な熱解析のための提案手法の有効性を示しており、最適化された設計と効率的な冷却システムにつながる。

8. 参考文献:

• [1] A. Chiba, K. Kiyota, N. Hoshi, M. Takemoto, and S. Ogasawara, 'Development of a Rare-Earth-Free SR Motor With High Torque Density for Hybrid Vehicles', IEEE Trans. Energy Convers., vol. 30, no. 1, pp. 175-182, Mar. 2015, doi: 10.1109/TEC.2014.2343962.
• [2] M. Morimoto, 'Iron loss of non-rare earth traction motor for electric vehicle', in 2010 IEEE Vehicle Power and Propulsion Conference, Lille, France: IEEE, Sep. 2010, pp. 1-4. doi: 10.1109/VPPC.2010.5729030.
• [3] N. G. Ozcelik, U. E. Dogru, M. Imeryuz, and L. T. Ergene, 'Synchronous Reluctance Motor vs. Induction Motor at Low-Power Industrial Applications: Design and Comparison', Energies, vol. 12, no. 11, p. 2190, Jun. 2019, doi: 10.3390/en12112190.
• [4] J. D. Widmer, R. Martin, and M. Kimiabeigi, 'Electric vehicle traction motors without rare earth magnets', Sustainable Materials and Technologies, vol. 3, pp. 7-13, Apr. 2015, doi: 10.1016/j.susmat.2015.02.001.
• [5] T. Wolnik, P. Dukalski, B. Będkowski, T. Jarek 'Selected aspects of designing motor for direct vehicle wheel drive', Przeglad Elektrotechniczny, vol. 1, no. 4, pp. 152-155, Apr. 2020, doi: 10.15199/48.2020.04.31.
• [6] Y. Xia, Y. Han, Y. Xu, and M. Ai, 'Analyzing Temperature Rise and Fluid Flow of High-Power-Density and High-Voltage Induction Motor in the Starting Process', IEEE Access, vol. 7, pp. 35588-35595, 2019, doi: 10.1109/ACCESS.2019.2899346.
• [7] P. Dukalski and R. Krok, 'Selected Aspects of Decreasing Weight of Motor Dedicated to Wheel Hub Assembly by Increasing Number of Magnetic Poles', Energies, vol. 14, no. 4, p. 917, Feb. 2021, doi: 10.3390/en14040917.
• [8] T. Wolnik, V. Styskala, and T. Micak, 'Study on the Selection of the Number of Magnetic Poles and the Slot-Pole Combinations in Fractional Slot PMSM Motor with a High Power Density', Energies, vol. 15, no. 1, p. 215, Dec. 2021, doi: 10.3390/en15010215.
• [9] J. Madej and B. Będkowski, 'Air flow analysis for electrical motor's cooling system with autodesk simulation CDF 2013 program', Acta Mechanica et Automatica, vol. 7, no. 2, pp. 89-92, Jun. 2013, doi: 10.2478/ama-2013-0016.
• [10] B. Będkowski and J. Madej, 'The innovative design concept of thermal model for the calculation of the electromagnetic circuit of rotating electrical machines', Eksploatacja i Niezawosność, vol. 17, no. 4, pp. 481-486, Sep. 2015, doi: 10.17531/ein.2015.4.1.
• [11] T. Wolnik, 'LEMOK – silnik o dużej gęstości mocy', Maszyny Elektryczne - Zeszyty Problemowe, no. 1(127), 2022, pp. 107-110.
• [12]T. Wolnik, T. Jarek, J. Golec, R. Topolewski, and D. Jastrzębski, 'High Power Density Motor for Light Electric Aircraft – Design Study and Lab Tests', in 2023 IEEE Workshop on Electrical Machines Design, Control and Diagnosis (WEMDCD), Newcastle upon Tyne, United Kingdom: ΙΕΕΕ, Apr. 2023, pp. 1-6. doi: 10.1109/WEMDCD55819.2023.10110934.
• [13] B. Bedkowski, P. Dukalski, T. Jarek, and T. Wolnik, 'Numerical model for thermal calculation analysis of the wheel hub motor for electric car verified by laboratory tests', IOP Conf. Ser.: Mater. Sci. Eng., vol. 710, no. 1, p. 012018, Dec. 2019, doi: 10.1088/1757-899X/710/1/012018.
• [14]P. Dukalski and B. Będkowski, 'Obliczenia cieplne silnika elektrycznego do zabudowy w piaście koła samochodu' Napędy i Sterowanie, vol. 24, no.7/8, pp. 70-76.
• [15]Ł. Cyganik and B. Będkowski, 'Układ mechaniczny przełączania zazębienia pomiędzy silnikiem elektrycznym, przekładnią planetarną oraz piastę koła w napędzie elektrycznym zabudowanym w kole pojazdu' Maszyny Elektryczne - Zeszyty Problemowe, no. 1(127), 2022, pp. 117-122.
• [16] B. Będkowski, J. Madej, 'Wyznaczenie zastępczej rezystancji cieplnej izolacji żłobkowej badania I symulacje Maszyny Elektryczne - Zeszyty Problemowe, 2(106), 2015, pp. 117-122.
• [17]P. Mynarek, 'Zastosowanie metody homogenizacji do wyznaczania współczynnika przewodnictwa cieplnego w silnikach elektrycznych', Przegląd Elektrotechniczny, vol. 1, no. 1, pp. 183-186, Jan. 2017, doi: 10.15199/48.2017.01.44.
• [18]P. Mynarek and M. Kowol, 'Metoda homogenizacji uzwojeń wsypywanych W maszynach elektrycznych' Maszyny Elektryczne - Zeszyty Problemowe, 1(105), 2015, pp. 149-154.
• [19] G. Kondziołka, 'Kryteria doboru syciw oraz lakierów elektroizolacyjnych' Maszyny Elektryczne - Zeszyty Problemowe, 2(102), 2014, pp. 7-10.
• [20]S. Opach, 'Obliczenia wartości zastępczej rezystancji cieplnej szczeliny powietrznej w wirnikowych maszynach elektrycznych, Maszyny Elektryczne - Zeszyty Problemowe, no. 1(127), 2022, pp. 101-105.
• [21]D. A. Howey, P. R. N. Childs, and A. S. Holmes, 'Air-Gap Convection in Rotating Electrical Machines', IEEE Trans. Ind. Electron., vol. 59, no. 3, pp. 1367-1375, Mar. 2012, doi: 10.1109/ΤΙΕ.2010.2100337.

9. 著作権:

• この資料は、"Szczepan Opach, Tomasz Wolnik"による論文です。「"Parametrization of the thermal model of induction motor with outer rotor"」に基づく。
• 論文の出典: doi:10.15199/48.2023.12.45

この資料は上記の論文に基づいて要約したものであり、商業目的での無断利用は禁止されています。
Copyright © 2025 CASTMAN. All rights reserved.