이 기술 브리핑은 Lin-Lin Chen, Shuo-Yan Chou, Tony C. Woo가 저술하여 Computer-Aided Design(1993)에 발표한 학술 논문 "Parting directions for mould and die design"을 기반으로 합니다. HPDC 전문가를 위해 CASTMAN의 전문가들이 요약하고 분석했습니다.
키워드
- 주요 키워드: 파팅 방향 최적화
- 보조 키워드: 다이캐스팅, 사출 성형, 금형 설계, 언더컷 및 코어, 계산 기하학, 가시성 맵, 이형성
핵심 요약
- 과제: 금형의 최적 파팅 방향을 선택하는 것은 매우 중요한 설계 단계입니다. 최적이 아닌 선택은 더 많은 언더컷을 유발하여 생산을 지연시키고 툴링 비용을 증가시키는 복잡하고 값비싼 코어를 필요로 합니다.
- 방법: 연구진은 계산 기하학을 사용하여 결정론적 알고리즘을 개발했습니다. 이 방법은 부품의 3D 모델을 분석하고, 각 형상에 대해 가능한 모든 이형 방향을 식별하여 이를 구(sphere) 상에 "가시성 맵(visibility maps)"으로 표현합니다.
- 핵심 혁신: 이 논문은 기존의 시행착오나 경험적 방법을 넘어, 필요한 코어의 수를 최소화하는 최상의 파팅 방향 쌍을 수학적으로 결정할 수 있는 체계적인 알고리즘을 제시합니다.
- 결론: 이 기하학적 알고리즘을 적용함으로써 제조업체는 툴링 비용을 절감하고, 금형 구조와 작동을 단순화하며, 생산 주기를 단축할 수 있습니다.
과제: 이 연구가 HPDC 전문가에게 중요한 이유
다이캐스팅 및 사출 성형에서 파팅 방향의 선택은 전체 제조 공정에 영향을 미치는 기본적인 단계입니다.. 성형된 부품은 금형의 두 반쪽에서 쉽게 추출되어야 합니다. 이러한 직선 이동을 방해하는 오목한 부분이나 돌출부, 즉 언더컷은 사이드 코어, 핀 또는 인서트의 사용을 필요로 합니다.. 이러한 장치들은 필수적이지만, 상당한 비용을 추가하고 금형의 설계와 작동을 복잡하게 만들며 전반적인 생산 속도를 저하시킵니다..
수십 년 동안 엔지니어들은 이 중요한 결정을 내리기 위해 경험, 경험적 방법 또는 세 가지 주축으로 파팅 방향을 제한하는 것과 같은 단순화된 가정에 의존해 왔습니다. [6-8]. 이러한 접근 방식의 단점은 불확실성입니다. 더 나은 해결책이 존재하는지, 또는 어떤 경우에는 실현 가능한 방향을 찾을 수 있는지조차 알 수 없습니다.. 이 연구는 입증 가능한 최적의 파팅 방향 쌍을 찾기 위한 결정론적 방법을 개발하여 이 문제를 정면으로 다룹니다.
접근 방식: 방법론 분석
최적의 파팅 방향을 찾기 위해 연구진은 계산 기하학에 기반한 새로운 접근 방식을 개발했습니다. 핵심 원리는 "완전한 가시성(complete visibility)" 개념과 직접적으로 관련된 "이형성(demouldability)"입니다. 표면은 특정 방향에서 완전히 보일 때, 즉 부품 자체가 제거를 방해하지 않을 때 그 방향으로 이형이 가능한 것으로 간주됩니다.
이 방법론은 세 가지 주요 단계로 구성됩니다:
- 포켓으로의 분해: 알고리즘은 먼저 객체의 기하학적 구조를 분석하여 이를 "포켓(pockets)" 집합으로 분해합니다. 포켓은 언더컷을 포함할 수 있는 오목한 부분이나 형상입니다 (그림 6).
- 가시성 맵(VMap) 생성: 각 포켓에 대해 연구진은 "가시성 맵(VMap)"을 계산합니다. 이는 해당 포켓이 코어 없이 완전히 보이고 이형 가능한 모든 방향의 집합을 나타내는 고유한 구면 영역입니다 (그림 9).
- 최적 방향 탐색: 그런 다음 문제는 기하학적 탐색 문제로 변환됩니다. 알고리즘은 구 상에서 이러한 VMap을 최대한 많이 포함하거나 "커버"하는 한 쌍의 반대 지점(파팅 방향을 나타냄)을 찾습니다. 커버되지 않은 VMap에 해당하는 포켓들이 코어를 필요로 하게 됩니다.
혁신: 주요 발견 및 데이터
이 논문의 주요 혁신은 코어 사용을 최소화하는 최적의 파팅 방향을 보장하는 강력한 알고리즘의 개발입니다. 이 알고리즘은 복잡한 제조 문제를 해결 가능한 기하학적 문제로 효과적으로 변환합니다.
- 발견 1: 결정론적 해결책: 이 연구는 추측을 넘어섭니다. 알고리즘은 그림 10의 구면 분할에서 볼 수 있듯이 모든 가능한 방향을 체계적으로 분할하고 가장 많은 기하학적 형상을 커버하는 쌍을 식별함으로써 명확한 해답을 제공합니다.
- 발견 2: 기하학적 커버리지를 통한 코어 최소화: 이 연구는 필요한 코어의 수가 선택된 파팅 방향에 의해 커버되지 않는 포켓의 수와 직접적으로 관련이 있음을 보여줍니다. 최대 개수의 VMap을 커버하는 방향을 찾음으로써 알고리즘은 본질적으로 코어의 수를 최소화합니다. 예를 들어, 그림 10에서 방향
d와 그 반대 방향은 포켓 S₁, S₂, S₄를 커버하므로 S₃만 코어로 형성하면 됩니다. - 발견 3: 효율적인 알고리즘: 저자들은 m개의 포켓과 n개의 정점을 가진 객체에 대해 O(nm log m)의 시간 복잡도를 갖는 알고리즘을 개발했습니다. 이는 복잡한 산업용 부품을 분석하는 데 이 접근 방식을 계산적으로 실현 가능하게 만듭니다.
HPDC 제품을 위한 실질적 시사점
논문의 결과와 결론에 엄격하게 근거할 때, 이 연구는 현대 제조 운영에 직접적이고 가치 있는 시사점을 제공합니다.
- 금형 설계: 이 연구는 금형 설계 단계를 위한 강력한 분석 도구를 제공합니다. 설계자는 직관에 의존하는 대신 이 알고리즘 접근 방식을 사용하여 부품의 기하학적 구조를 분석하고 강재를 가공하기 전에 최적의 파팅 전략을 명확하게 식별할 수 있습니다. 이를 통해 비용이 많이 드는 재설계와 불필요하게 복잡하고 비싼 툴링 제작을 방지할 수 있습니다.
- 공정 엔지니어: "파팅 방향" 섹션의 연구 결과는 계산적으로 결정된 파팅 방향 선택이 코어 수를 직접적으로 최소화할 수 있음을 시사합니다. 이는 금형의 기계적 작동을 단순화하여 잠재적으로 사이클 타임을 줄이고 기계적 고장 가능성을 낮추며 전체 생산 공정을 간소화할 수 있습니다.
- 비용 추정: 설계 단계에서 필요한 최소 코어 수를 결정할 수 있는 능력은 더 정확하고 경쟁력 있는 견적을 가능하게 합니다. 필요한 툴링의 실제 복잡성을 조기에 파악함으로써 예상치 못한 비용과 지연을 피할 수 있습니다.
논문 상세 정보
Parting directions for mould and die design
1. 개요:
- 제목: Parting directions for mould and die design (금형 및 다이 설계를 위한 파팅 방향)
- 저자: Lin-Lin Chen, Shuo-Yan Chou, and Tony C. Woo
- 발행 연도: 1993
- 학술지/학회: Computer-Aided Design, Volume 25, Number 12
- 키워드: manufacturing, algorithms, computational geometry, injection moulding, die casting, parting directions, visibility
2. 초록:
이형성의 조건을 기반으로 완전 가시성과 부분 가시성이라는 두 가지 수준의 가시성을 정의합니다. 표면이 완전히 보이는 시야 방향은 단위 구 상에서 가시성 맵(visibility map)이라 불리는 볼록 영역으로 표현될 수 있습니다. 주어진 객체를 포켓으로 나누고, 각 포켓의 가시성과 이형성을 독립적으로 결정하며, 가시성 맵을 구성하고, 코어 수를 최소화하는 최적의 파팅 방향 쌍을 선택하는 알고리즘을 제시합니다. 예제를 통해 알고리즘을 설명합니다.
3. 서론:
다이캐스팅 및 사출 성형에서 기본 금형은 한 쌍의 반대되는 파팅 방향을 따라 분리되는 두 개의 플레이트로 구성됩니다. [1-4]. 부품의 제거를 방해하는 형상, 즉 언더컷은 코어의 사용을 필요로 하며, 이는 툴링 비용을 증가시키고 공정을 복잡하게 만듭니다.. 이 논문은 이 단계의 자동화에 대한 이전 연구들이 주축을 따른 파팅 방향을 가정하거나 경험적 방법을 사용하는 등 제한적이었으며, 더 나은 해결책이 있는지 알 수 없었다고 지적합니다. [6-10]. 본 논문은 코어 수를 최소화하는 최적의 파팅 방향 쌍을 찾기 위한 결정론적 방법을 제시합니다.
4. 연구 요약:
연구 주제의 배경:
파팅 방향의 선택은 필요한 코어의 수와 모양을 결정하는 중요한 금형 설계 단계입니다. 비용과 복잡성을 줄이기 위해 코어를 최소화하는 것이 일반적인 원칙입니다..
이전 연구 현황:
이 단계를 자동화하려는 과거의 접근 방식은 제한적이었습니다. 파팅 방향의 선택을 몇 개의 주축으로 제한하거나, 무작위 방향에서 선택하거나, 경험적 방법을 사용했습니다. [6-10]. 이러한 방법들은 실현 가능한 해결책은 물론 최적의 해결책을 찾는 것을 보장할 수 없었습니다.
연구 목적:
주어진 객체의 기하학적 구조에 대해 필요한 코어 수를 최소화하는 것을 목표로 최적의 파팅 방향 쌍을 찾기 위한 결정론적 방법을 개발하는 것입니다.
핵심 연구:
연구의 핵심은 파팅 방향 문제를 "대척점에 의한 구면 다각형 커버링(spherical polygon covering by antipodes)"이라는 기하학적 문제로 공식화한 것입니다. 연구진은 객체를 포켓으로 분해하고, 그들의 가시성 맵(VMap)을 계산한 후, 이러한 VMap을 최대로 커버하는 한 쌍의 반대 방향을 찾아 코어의 필요성을 최소화하는 알고리즘을 개발했습니다.
5. 연구 방법론
연구 설계:
이 연구는 계산 기하학에 기반한 이론적, 알고리즘적 접근 방식을 사용합니다. 시야 방향에서의 "완전한 가시성" 측면에서 이형성을 정의합니다. 객체는 가시성을 독립적으로 처리할 수 있는 분리된 "포켓"으로 분해됩니다.
데이터 수집 및 분석 방법:
이 방법은 각 포켓의 가시성을 단위 구에 매핑하여 "가시성 맵(VMap)"을 생성하는 것을 포함합니다. 그런 다음 문제는 구 상에서 이러한 VMap 내에 포함된 최대 개수의 점을 찾는 것으로 해결됩니다. VMap에 의해 유도된 구면 분할을 계산하고 최적의 점(방향)을 찾기 위해 순회하는 알고리즘이 제시됩니다.
연구 주제 및 범위:
이 연구는 다면체 객체에 초점을 맞추고 최적의 단일 파팅 방향 쌍을 찾는 것을 목표로 합니다. 모든 코어가 동일하게 바람직하지 않다고 가정하고 코어 수를 최소화하는 것을 주요 목표로 합니다.
6. 주요 결과:
주요 결과:
주요 결과는 m개의 포켓과 n개의 정점을 가진 객체에 대한 최적의 파팅 방향을 결정하기 위한 O(nm log m) 시간 복잡도의 알고리즘입니다. 이 알고리즘은 부품의 기하학적 구조를 기반으로 코어 수를 최소화하는 해결책을 보장합니다. 논문은 알고리즘이 구면 분할에서 최대로 커버된 점을 찾아 최적의 방향을 식별하는 방법을 단계별 예제(그림 6, 9, 10)를 통해 설명합니다.
그림 이름 목록:
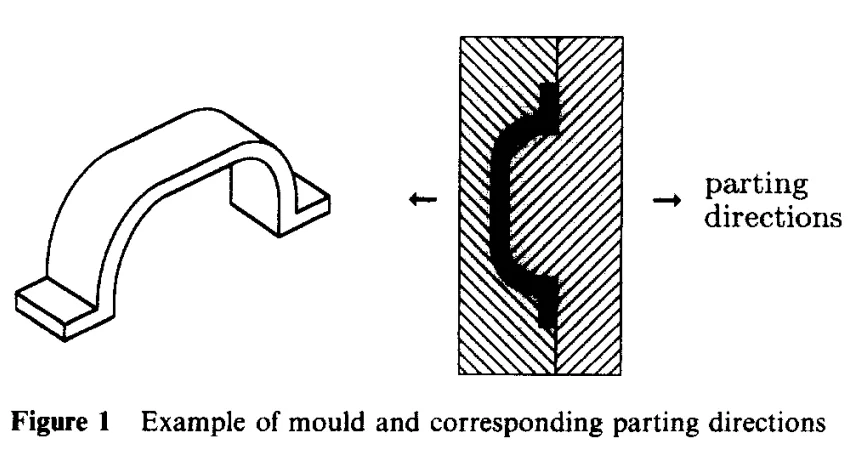
- 그림 1: 금형 및 해당 파팅 방향의 예
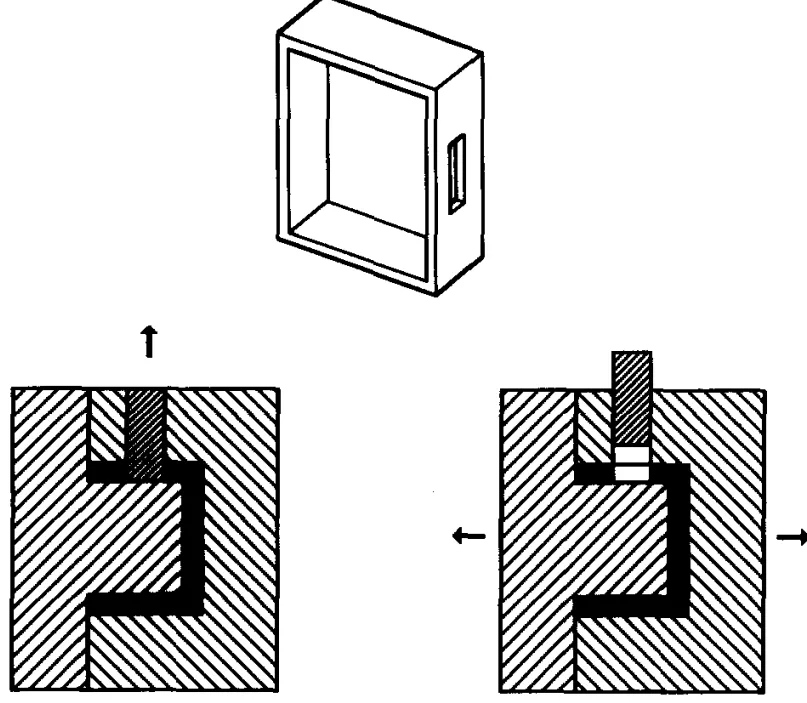
- 그림 2: 외부 리세스를 위한 사이드 코어가 필요한 객체의 예
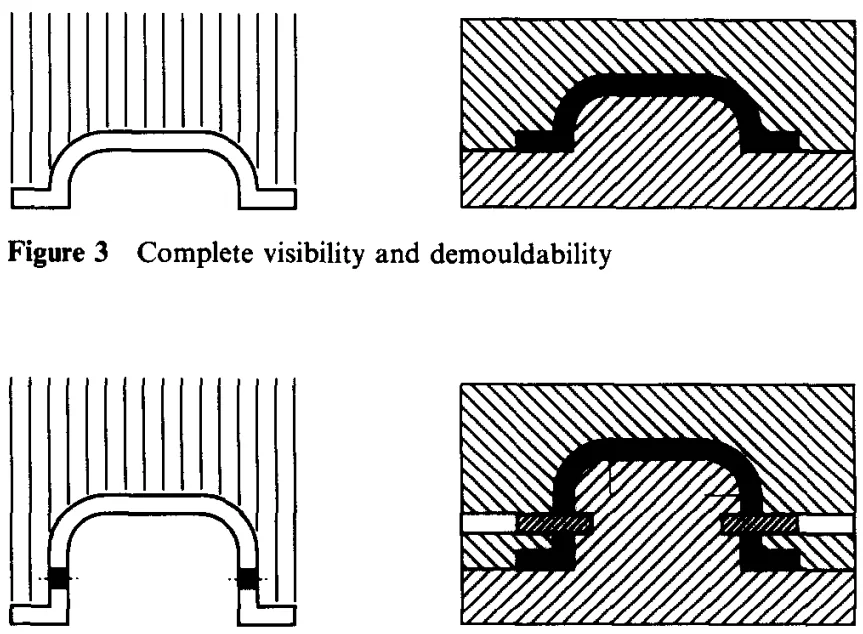
- 그림 3: 완전한 가시성 및 이형성
- 그림 4: 부분적 가시성 및 코어 사용
- 그림 5: 표면과 해당 GMap 및 VMap의 예
- 그림 6: 객체; (a) 객체, (b) 볼록 포락선, (c) 해당 밀봉된 포켓, (d) 포켓
- 그림 7: 대척점에 의한 구면 다각형 커버링
- 그림 8: 두 인접 셀과 그 소유권 벡터
- 그림 9: 그림 6의 객체 포켓과 해당 VMap
- 그림 10: 그림 9의 VMap과 그 반대 방향에 의해 유도된 구면 분할
7. 결론:
코어를 최소화하기 위해 최적의 파팅 방향을 결정하는 O(nm log m) 시간 복잡도의 알고리즘이 개발되었습니다. 논문은 복잡성이나 비용에 따라 다른 포켓에 다른 가중치를 할당하도록 알고리즘을 수정할 수 있다고 언급합니다. 완전히 보이지 않는 포켓에는 코어가 사용된다는 가정이 명시되어 있습니다. 저자들은 향후 연구에서 부분 가시성을 호출하여 포켓을 세분화함으로써 코어를 추가로 제거하는 방법을 탐색할 수 있다고 제안합니다.
8. 참고 문헌:
(참고 문헌 목록은 원본과 동일하게 영문으로 유지합니다.)
- Bralla, J G (Ed.) Handbook of Product Design for Manufacturing: A Practical Guide to Low-Cost Production McGraw-Hill (1986)
- Campbell, J Castings Butterworth-Heinemann (1991)
- Pye, R G W Injection Mold Design: A Textbook for the Novice and a Design Manual for the Thermoplastics Industry (4th Ed.) John Wiley (1989)
- Rubin, I I Handbook of Plastic Materials and Technology John Wiley (1990)
- Kalpakjian, S Manufacturing Processes for Engineering Materials Addison-Wesley (1991)
- Lee, K and Smith, C T 'Computer-aided pattern design for casting processes' Manufacturing Processes, Systems & Machines Proc. 14th Conf. Production Research & Technology (1987) pp 365-371
- Ravi, B and Srinivasan, M N 'Decision criteria for computer-aided parting surface design' Comput.-Aided Des. Vol 22 No 1 (1990) pp 11-18
- Smith, C T and Lee, K 'Computer-aided pattern design for casting processes' AFS Trans. (1986) pp 21-28
- Ganter, M A and Tuss, L L 'Computer-assisted parting line development for cast pattern production' AFS Trans. (1990) pp 795-800
- Hui, K C and Tan, S T 'Mould design with sweep operations - a heuristic search approach' Comput.-Aided Des. Vol 24 No 2 (1992) pp 81-91
- O'Rourke, J Art Gallery Theorems and Algorithms Oxford University Press (1987)
- Toussaint, G T 'Computing visibility properties of polygons' in Pattern Recognition and Artificial Intelligence North-Holland (1988)
- Stolfi, J Oriented Projective Geometry: A Framework for Geometric Computations Academic Press (1991)
- Struik, D J Lectures on Analytic and Projective Geometry Addison-Wesley (1953)
- Hilbert, D and Cohn-Vossen, S Geometry and the Imagination Chelsea (1952)
- Chen, L L and Woo, T C 'Computational geometry on the sphere for automated machining' ASME J. Mech. Des. Vol 114 No 2 (1992) pp 288-295
- Hoffmann, C M Geometric and Solid Modeling: An Introduction Morgan Kaufmann (1989)
- Edelsbrunner, H Algorithms in Combinatorial Geometry Springer-Verlag (1987)
- Preparata, F P and Hong, S J 'Convex hulls of finite sets of points in two and three dimensions' Commun. ACM Vol 2 No 20 (1977) pp 87-93
- Tang, K and Woo, T C 'Algorithmic aspects of alternating sums of volumes. Part 1: Data structure and difference operation' Comput.-Aided Des. Vol 23 No 5 (1991) pp 357-366
전문가 Q&A: 자주 묻는 질문에 대한 답변
Q1: 이 연구에서 코어를 최소화하기 위해 가장 중요하게 식별된 단일 요소는 무엇이었습니까?
A1: 이 연구는 가장 중요한 요소가 최대 개수의 가시성 맵(VMap)에 포함되는 한 쌍의 대척 파팅 방향(p와 -p)을 찾는 것이라고 결론지었습니다. 이는 가장 많은 수의 부품 형상이 코어 없이 이형될 수 있도록 보장합니다. [Parting directions for mould and die design, "Parting Directions" 섹션, 그림 7].
Q2: 이 연구는 이 문제를 해결하기 위한 전통적인 방법과 어떻게 비교됩니까?
A2: 논문의 서론에서는 전통적인 방법이 종종 경험적 방법에 의존하거나 세 가지 주축만 테스트하는 데 국한된다고 언급합니다. [6-8]. 이 연구는 모든 가능한 방향을 분석하고 최적의 해결책을 찾는 것을 보장하는 결정론적 알고리즘을 도입하여 이전 접근 방식의 불확실성을 크게 개선했습니다. [Parting directions for mould and die design, "Introduction" 섹션].
Q3: 이 발견은 모든 종류의 합금에 적용됩니까, 아니면 특정 합금에만 적용됩니까?
A3: 이 연구는 순전히 기하학적이며 "다면체 객체"의 모양에 초점을 맞춥니다. 이는 재료와는 무관합니다. 따라서 이 알고리즘은 주조되는 특정 합금에 관계없이 모든 부품의 기하학적 구조에 적용할 수 있습니다. [Parting directions for mould and die design, "Visibility and Demouldability" 섹션].
Q4: 연구진이 이 결론에 도달하기 위해 사용한 구체적인 측정 또는 시뮬레이션 기술은 무엇이었습니까?
A4: 연구진은 계산 기하학 기술을 활용했습니다. 구체적으로, 그들은 가우스 구 상에 부품 형상에 대한 "가시성 맵(VMap)"을 생성하여 문제를 모델링한 다음, 최적의 방향을 찾기 위해 "점에 의한 구면 다각형 커버링" 알고리즘을 개발했습니다. [Parting directions for mould and die design, "Algorithm (spherical polygon covering by a point)" 섹션].
Q5: 논문에 따르면, 주요 한계점이나 향후 연구 분야는 무엇입니까?
A5: 저자들은 결론에서 주요 한계점은 모든 코어가 동일하게 바람직하지 않다고 가정한 것이라고 말합니다. 그들은 향후 연구가 비용이나 복잡성에 따라 가중치가 부여된 포켓을 처리하도록 알고리즘을 수정하고, 포켓을 세분화하여 코어의 필요성을 완전히 제거하는 방법을 탐색하는 데 초점을 맞춰야 한다고 제안합니다. [Parting directions for mould and die design, "Conclusions" 섹션].
Q6: 이 논문이 다이캐스팅 시설에 주는 직접적이고 실용적인 교훈은 무엇입니까?
A6: 핵심 교훈은 부품의 기하학적 구조를 분석하기 위해 계산 알고리즘을 사용함으로써 코어 수를 명확하게 최소화하는 최적의 파팅 방향을 결정할 수 있다는 것입니다. 이는 직접적으로 툴링 비용 절감, 더 단순한 금형, 그리고 더 효율적인 생산 주기로 이어집니다. [Parting directions for mould and die design, "Conclusions" 섹션].
결론 및 다음 단계
이 연구는 HPDC에서 금형 설계를 향상시키기 위한 귀중한 로드맵을 제공합니다. 경험 기반 결정에서 데이터 기반의 기하학적 알고리즘으로 전환함으로써, 이 연구 결과는 품질을 개선하고, 툴링 비용을 절감하며, 생산을 최적화하는 명확한 길을 제시합니다.
CASTMAN은 고객의 가장 어려운 다이캐스팅 문제를 해결하기 위해 최신 산업 연구를 적용하는 데 전념하고 있습니다. 이 논문에서 논의된 문제가 귀사의 운영 목표와 관련이 있다면, 저희 엔지니어링 팀에 연락하여 귀사의 부품에 이러한 고급 원칙을 구현하는 방법을 논의하십시오.
저작권
- 이 자료는 "Lin-Lin Chen, Shuo-Yan Chou, and Tony C. Woo"의 논문입니다. "Parting directions for mould and die design"을 기반으로 합니다.
- 논문 출처: Computer-Aided Design, Volume 25, Number 12, December 1993. 문서에 특정 DOI URL이 제공되지 않았습니다.
이 자료는 정보 제공 목적으로만 사용됩니다. 무단 상업적 사용을 금지합니다.
Copyright © 2025 CASTMAN. All rights reserved.