복잡 부품의 사출 성형에서 자동화된 측면 동작 설계를 위한 기하학적 알고리즘

이 연구는 복잡한 부품 제조의 중요한 측면을 다루며, 금형 설계를 간소화하고 생산 비용을 최적화하는 방법을 제시합니다.

1. 개요:

• 제목: 복잡 부품의 사출 성형에서 자동화된 측면 동작 설계를 위한 기하학적 알고리즘 (Geometrical algorithms for automated design of side actions in injection moulding of complex parts)
• 저자: 아시스 고팔 바네르지 (Ashis Gopal Banerjee), 사티안드라 K. 굽타 (Satyandra K. Gupta)
• 발행 연도: 2007년
• 발행 저널/학회: Computer-Aided Design
• 키워드: 기하학적 알고리즘, 자동화 설계, 측면 동작, 사출 성형, 언더컷, 비용 함수

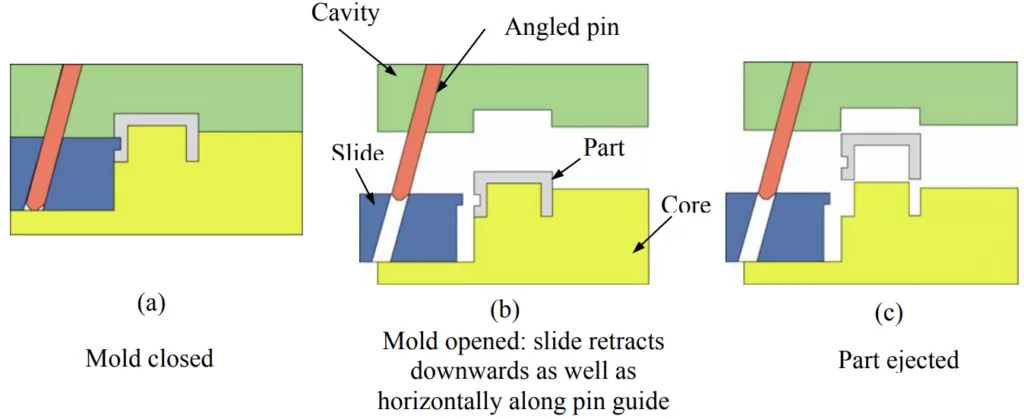
2. 연구 배경:

• 연구 주제의 사회적/학문적 맥락: 복잡한 사출 성형 부품에는 주 금형 개방 방향으로 접근할 수 없는 언더컷이라는 특징이 자주 포함됩니다. 측면 동작은 보조 금형 부품으로 이러한 언더컷을 형성하는 데 필수적입니다. 그러나 측면 동작을 수동으로 설계하는 것은 "상당한 전문 지식"을 요구하는 "어려운 작업"입니다. 이러한 수동 프로세스는 추가 제조, 조립 및 더 긴 성형 사이클 시간으로 인해 금형 비용 증가에 기여합니다. 따라서 측면 동작 설계 자동화는 금형 설계 리드 타임을 단축하고 전체 사출 성형 프로세스를 최적화하는 데 매우 중요합니다.
• 기존 연구의 한계: 기존의 측면 동작 설계 방법은 종종 최적의 솔루션을 제공하는 데 부족합니다. 복잡한 언더컷 영역이 (1) 측면 동작을 생성하기 위해 분할되어야 하거나, (2) 유한한 접근성을 갖거나, (3) 성형이 불가능하여 부품 재설계가 필요한 경우 "만족스럽게 작동하지 않습니다 (즉, 가능한 솔루션의 포괄적인 집합에서 최적의 솔루션을 생성할 수 없습니다)." 많은 방법이 "휴리스틱 방향"에 의존하며 금형 부품 간섭을 검증하기 위해 "사후 처리 작업 (예: 시뮬레이션)"이 필요할 수 있습니다.
• 연구의 필요성: 이 연구는 수동 방법 및 기존 자동화 접근 방식의 한계를 극복하기 위해 자동화된 측면 동작 설계의 필요성을 다룹니다. 자동화된 설계는 "금형 설계 리드 타임을 크게 단축"하고 "사용자 정의 가능한 성형 비용 함수"를 최소화하여 프로세스를 최적화할 것을 약속합니다. 이 연구는 사출 성형 기술을 발전시키고 복잡한 부품의 효율적인 제조를 가능하게 하는 데 필수적입니다.

3. 연구 목적 및 연구 질문:

• 연구 목적: 주요 연구 목적은 "사용자 정의 가능한 사출 성형 비용 함수를 최소화하기 위해 측면 동작의 형상을 생성하는 알고리즘을 설명하는 것"입니다. 이 논문은 기존 방법이 복잡한 언더컷 영역에 부적절한 경우에 "이러한 유형의 사례를 처리하기 위한 새로운 알고리즘을 제시하는 것"을 목표로 합니다.
• 주요 연구 질문: 이 연구는 다음 질문에 대한 답을 찾고자 합니다.
  • 기하학적 알고리즘은 언더컷이 있는 복잡한 사출 성형 부품에 대한 측면 동작 설계를 어떻게 자동화할 수 있는가?
  • 사용자 정의 가능한 성형 비용 함수는 측면 동작 설계를 최적화하기 위해 자동화된 설계 프로세스에 어떻게 통합될 수 있는가?
  • 분할이 필요하거나 접근성이 제한적인 복잡한 언더컷 영역은 알고리즘적으로 어떻게 효과적으로 처리될 수 있는가?
• 연구 가설: 명시적으로 언급되지는 않았지만, 근본적인 가설은 "이 논문에 제시된 결과가 측면 동작 설계를 위한 완전 자동화된 소프트웨어 개발의 기초를 제공할 것"이라는 것입니다. 저자들은 기하학적 알고리즘이 측면 동작 설계를 자동화하고, 복잡한 언더컷 형상을 효과적으로 처리하며, 사용자 정의 가능한 성형 비용 함수를 최소화하기 위해 개발될 수 있다고 제안합니다.

4. 연구 방법론

• 연구 설계: 이 연구는 전산 기하학 기반 접근 방식을 채택하여 자동화된 측면 동작 설계를 위한 기하학적 알고리즘의 개발 및 구현에 중점을 둡니다.
• 데이터 수집 방법: 이 연구는 다면체 부품 및 금형 외함의 기하학적 모델을 입력으로 사용합니다. 개발된 알고리즘을 테스트하고 검증하기 위해 전산 실험이 수행됩니다.
• 분석 방법: 알고리즘은 계산 시간, 검색 공간의 노드 수, 분기 계수와 같은 지표를 기반으로 성능을 평가하여 전산 실험을 통해 분석됩니다. "깊이 우선 분기 한정 알고리즘", "민코프스키 합", "충돌 감지", "스윕 기반 충돌 다각형"과 같은 방법이 알고리즘 내에서 사용됩니다.
• 연구 대상 및 범위: 이 연구는 사출 성형에서 "언더컷 면"이 있는 "다면체 부품"에 대한 측면 동작 설계에 중점을 둡니다. 범위는 "주 금형 개방 방향에 수직"으로 후퇴하는 측면 동작으로 제한되며, 주로 측면 동작 메커니즘으로 "슬라이더 및 리프터"에 초점을 맞춥니다.

5. 주요 연구 결과:

• 주요 연구 결과: 이 논문은 다음을 위한 알고리즘을 성공적으로 개발하고 제시했습니다.
  • "사용자 정의 가능한 사출 성형 비용 함수를 최소화하기 위해 측면 동작의 형상을 생성"
  • "모든 언더컷 면에 대한 후보 후퇴 공간 계산"
  • "실행 가능하고 비지배적인 후퇴의 이산 집합 생성"
  • "이러한 후퇴에 대한 상태 공간 검색을 수행하여 언더컷 면을 언더컷 영역으로 그룹화"
  • "개별 측면 동작의 형상 생성"
• 통계적/질적 분석 결과: 논문의 표 1은 다양한 복잡성을 가진 부품 모델에서 알고리즘의 성능을 정량화하는 "전산 실험 결과"를 제시합니다. 예를 들어, 파트 A 모델 #1의 경우 "후보 후퇴 공간 계산 시간"은 "3.5초 (in s)"로, "실행 가능한 후퇴 집합 생성 시간"은 "5.2초 (in s)"로 보고됩니다. 그림 15는 "비용 함수 매개변수를 수정하여 얻은 대안 설계"를 시각적으로 보여주며, 알고리즘의 다양한 비용 고려 사항에 대한 적응성을 보여줍니다.
• 데이터 해석: 표 1에 표시된 전산 결과는 제안된 알고리즘의 효율성과 타당성을 나타냅니다. 논문은 "주어진 비용 함수 매개변수 값에 따라 최적의 2개 또는 3개의 측면 동작 세트가 약 30-50초 만에 4개의 샘플 부품에 대해 생성되었다"고 강조하며 "합리적으로 좋은 성능"을 시사합니다. 그림 15는 사용자 정의된 비용 함수 매개변수를 기반으로 다양한 측면 동작 설계를 생성하는 알고리즘의 능력을 더욱 보여주며, 실제 적용 가능성을 입증합니다.
• 그림 목록:
  • Figure 1: Side action removal in a direction different from the main mold opening direction
  • Figure 2: Steps after part solidification for molding external undercuts using slider
  • Figure 3: Steps after part solidification for molding internal undercuts using lifters
  • Figure 4: Typical thin-walled plastic parts
  • Figure 5: Parts that pose challenges for existing side action design algorithms
  • Figure 6: Candidate and non-candidate core retractions
  • Figure 7: Candidate core retraction space
  • Figure 8: Difference between candidate and feasible core retractions
  • Figure 9: Intersection of two candidate retraction spaces
  • Figure 10: Maximum error in retraction length
  • Figure 11: Constructing collision-free 2D translation space
  • Figure 12: Constructing candidate core retraction space
  • Figure 13: Five test parts
  • Figure 14: Side action solids for 4 different test parts (A, B, C, D) shown in retracted state
  • Figure 15: Alternative designs obtained by modifying the cost function parameters

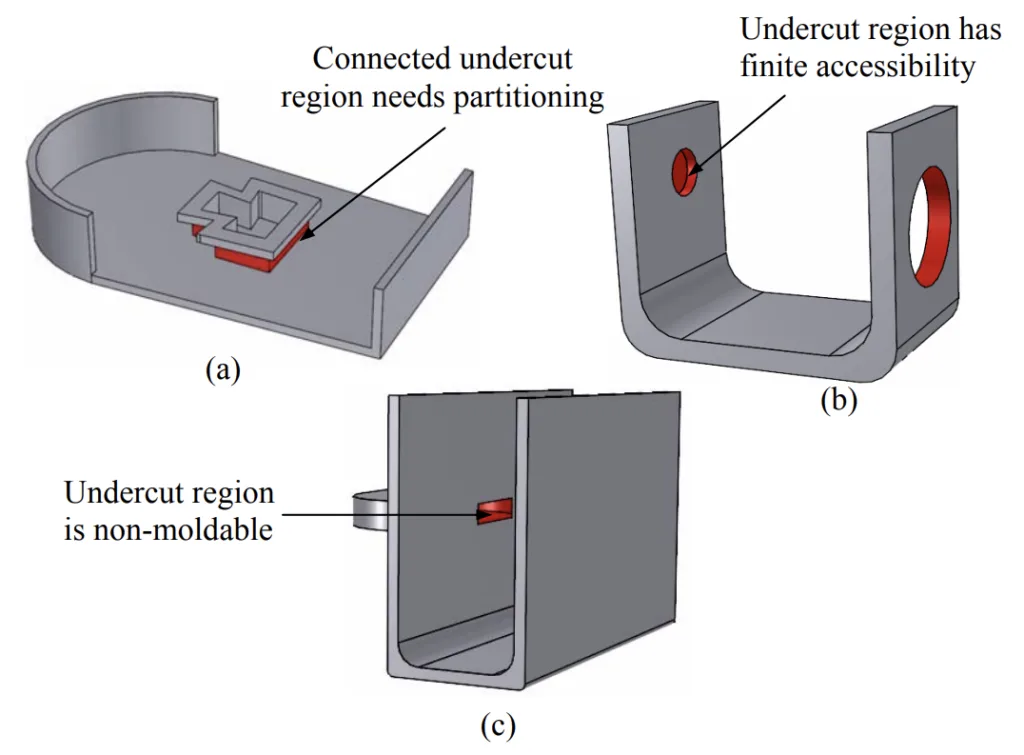
6. 결론 및 논의:

• 주요 결과 요약: 이 연구는 사출 성형에서 측면 동작 설계를 자동화하기 위한 새로운 알고리즘을 성공적으로 도입했습니다. 이러한 알고리즘은 복잡한 언더컷 형상을 효과적으로 처리하고 사용자 정의된 성형 비용 함수를 최소화합니다. 주요 알고리즘 단계에는 후보 후퇴 공간 계산, 실행 가능한 후퇴 선택, 언더컷 영역 그룹화 및 측면 동작 형상 생성이 포함됩니다. 전산 실험은 접근 방식의 타당성과 효율성을 검증합니다.
• 연구의 학문적 의의: 이 연구는 자동화된 금형 설계 분야에 중요한 학문적 기여를 합니다. 기존 방법의 한계를 극복하고 보다 최적화되고 포괄적인 솔루션을 제공하는 측면 동작 설계를 위한 강력한 알고리즘 프레임워크를 제공합니다.
• 실용적 의미: 개발된 알고리즘은 사출 성형 산업에 상당한 실용적 의미를 갖습니다. 이는 금형 설계 리드 타임을 획기적으로 단축하고, 설계 품질을 향상시키며, 제품 개발 주기를 가속화하고, 제조 비용을 절감할 수 있는 완전 자동화된 측면 동작 설계 소프트웨어 생성을 위한 길을 열어줍니다.
• 연구의 한계: 논문은 "현재의 목적 함수는 후퇴 방향을 고려하지 않는다"는 점을 인정하며, 향후 개선해야 할 영역을 시사합니다. 또한, 이 연구는 주로 "측면 코어" 유형의 측면 동작에 초점을 맞추고 있으며, "분할 코어, 융합 코어 등과 같은 다른 종류의 측면 동작을 설계하기 위해 방법을 일반화하는 추가 작업이 필요하다"는 것을 나타냅니다.

7. 향후 후속 연구:

• 후속 연구 방향: 논문은 다음과 같은 여러 가지 향후 연구 방향을 제시합니다.
  • "분할 코어, 융합 코어 등"과 같은 다른 유형의 측면 동작을 수용하도록 알고리즘을 일반화합니다.
  • 이론적 기반을 강화하기 위해 "에지 하위 분할 방식"을 개선합니다.
  • CAD 시스템과의 원활한 통합을 위해 "NURBS 표면에서 직접 측면 동작을 설계"하도록 접근 방식을 확장합니다.
  • 통합 최적화를 위해 "측면 동작 설계와 동시에 주 금형 개방 방향을 선택할 가능성"을 탐구합니다.
  • "측면 동작이 금형 개방 방향에 수직인 평면에서 반드시 후퇴할 필요는 없는 경우"를 처리하도록 알고리즘을 확장하고, 잠재적으로 3D 후퇴 공간 분석을 포함합니다.
• 추가 탐구가 필요한 영역: 후퇴 방향을 통합하도록 목적 함수를 개선하고, 알고리즘을 다양한 측면 동작 메커니즘으로 일반화하고, NURBS 기반 CAD 환경과 통합하고, 분할 방향과 측면 동작 설계를 동시에 최적화하고, 보다 복잡한 시나리오를 위해 3D 후퇴 공간 분석으로 접근 방식을 확장하는 데 추가 탐구가 필요합니다.

8. 참고 문헌:

• [1] H. K. Ahn, M. Berg, P. Bose, S. W. Cheng, D. Halperin, J. Matoušek, and O. Schwarzkopf. Separating an Object from Its Cast. Computer Aided Design, Vol. 34, No. 8, pp. 547-559, 2002.
• [2] B. Aronov, and M. Sharir. On Translational Motion Planning of a Convex Polyhedron in 3-Space. Siam Journal of Computing, Vol. 26, No. 6, pp. 1785-1803, 1997.
• [3] A. G. Banerjee. Computer Aided Design of Side Actions for Injection Molding of Complex Parts. Master of Science Thesis, University of Maryland, College Park, 2006.
• [4] Cgal.org. Computational Geometry Algorithms Library. http://www.cgal.org, 2004.
• [5] L.L. Chen, S.Y. Chou, and T.C. Woo. Parting Directions for Mould and Die Design. Computer Aided Design, Vol. 25, No. 12, pp. 762-768, 1993.
• [6] L.L. Chen, S. Y. Chou, and T. C. Woo. Partial Visibility for Selecting a Parting Direction in Mould and Die Design. Journal of Manufacturing Systems, Vol. 14, No. 5, pp. 319-330, 1995.
• [7] X. Chen and S. McMains. Finding All Undercut-free Parting Directions for Extrusions. Geometric Modeling and Processing, 2006, Lecture Notes in Computer Science, Vol. 4077, pp. 514-527, 2006.
• [8] Y. Chen, and D.W. Rosen. A Region Based Method to Automated Design of Multi-Piece Molds with Application to Rapid Tooling, Journal of Computing and Information Science in Engineering, Vol. 2, No. 2, pp. 86-97, 2002.
• [9] Y. Chen, and D.W. Rosen. A reverse glue approach to automated construction of multi-piece molds, Journal of Computing and Information Science in Engineering, Vol. 3, No. 3, pp. 219-230, 2003.
• [10] Y. H. Chen. Determining parting direction based on minimum bounding box and fuzzy logics. International Journal of Machine Tools and Manufacture, Vol. 37, No. 9, pp. 1187-1199, 1997.
• [11] T. H. Cormen, C. E. Leiserson, R. L. Rivest, and C. Stein. Introduction to Algorithms, The MIT Press, 2001.
• [12] M. de Berg, M. van Kreveld, M. Overmars, and O. Schwarzkopf. Computational geometry: algorithms and applications, Second Edition. Springer-Verlag, Berlin, 2000.
• [13] S. Dhaliwal, S.K. Gupta, J. Huang, and A. Priyadarshi. Algorithms for Computing Global Accessibility Cones. Journal of Computing and Information Science in Engineering, Vol. 3, No. 3, pp. 200-209, 2003.
• [14] G. Elber, X. Chen, and E. Cohen. Mold Accessibility via Gauss Map Analysis. Journal of Computing and Information Science in Engineering, Vol. 5, No. 2, pp. 79-85, 2005.
• [15] G. Fowler. Cost and Performance Evaluation Models For Comparing Traditional and Multi-Shot Injection Molding. Master of Science Thesis, University of Maryland, College Park, 2004.
• [16] M. W. Fu, J. Y. H. Fuh, and A. Y. C. Nee. Generation of optimal parting direction based on undercut features in injection molded parts. IIE Transactions Vol. 31, pp. 947-955, 1999.
• [17] M. W. Fu, J. Y. H. Fuh, and A. Y. C. Nee, Undercut Feature Recognition in an Injection Mould Design System. Computer Aided Design, Vol. 31, No. 12, pp. 777-790, 1999.
• [18] M. A. Ganter, and P. A. Skoglund. Feature extraction for casting core development. Journal of Mechanical Design, Vol. 115, No. 4, pp. 744-750, 1993.
• [19] S. K. Gupta, A. G. Banerjee, X. Li, and G. Fowler. Development of a Manufacturability Analysis Framework for Injection Molded Multi-Material Objects. In NSF Design, Service, and Manufacturing Grantees and Research Conference, St. Louis, MO, 2006.
• [20] J. Huang, S. K. Gupta, and K. Stoppel. Generating sacrificial multi-piece molds using accessibility driven spatial partitioning. Computer Aided Design, Vol. 35 No. 3, pp. 1147-1160, 2003.
• [21] K. C. Hui, and S. T. Tan. Mould design with sweep operations-a heuristic search approach. Computer Aided Design, Vol. 24, No. 2, pp. 81-91, 1992.
• [22] K C. Hui. Geometric Aspects of the Mouldability of Parts. Computer Aided Design, Vol. 29, No. 3, pp. 197-208, 1997.
• [23] L. Kettner. Software Design in Computational Geometry and Contour-Edge Based Polyhedron Visualization. Ph.D. Thesis, ETH Zurich, Switzerland, 1999.
• [24] R. Kharderkar, G. Burton, and S. McMains. Finding feasible mold parting directions using graphics hardware. Computer Aided Design, Vol. 38, No. 4, pp. 327-341, 2006.
• [25] W. T. Liou, J. J-M. Tan, and R. C. T. Lee. Minimum Rectangular Partition Problem for Simple Rectilinear Polygons. IEEE Transactions on Computer-Aided Design, Vol. 9, No. 7, pp. 720-733, 1990.
• [26] H. Y. Lu, and W. B. Lee. Detection of Interference Elements and Release Directions in Die-cast and Injection-moulded Components. Proceedings of the Institution of Mechanical Engineers, Part B Journal of Engineering Manufacture, Vol. 214, No. 6, pp. 431-441, 2000.
• [27] S. McMains and X. Chen. Finding Undercut-Free Parting Directions for Polygons with Curved Edges. Journal of Computing and Information Science in Engineering, Vol. 6, No. 1, pp. 60-68, 2006.
• [28] C. Poli. Design for Manufacturing, A Structured Approach. Butterworth-Heinemann: Boston, Massachusetts, 2001.
• [29] A. K. Priyadarshi, and S. K. Gupta. Geometric algorithms for automated design of multi-piece permanent molds. Computer Aided Design, Vol. 36, No. 3, pp. 241-260, 2004.
• [30] A. K. Priyadarshi, and S. K. Gupta. Finding Mold-Piece Regions Using Computer Graphics Hardware. Geometric Modeling and Processing, 2006, Lecture Notes in Computer Science, Vol. 4077, pp. 655-662, 2006.
• [31] D. Rappaport, and A. Rosenbloom. Moldable and castable polygons. Computational Geometry: Theory and Applications, Vol. 4, No. 4, pp. 219-233, 1994.
• [32] B. Ravi, and M. N. Srinivasan. Decision criteria for computer-aided parting surface design. Computer Aided Design, Vol. 22, No. 1, pp. 11-18, 1990.
• [33] K. H. Shin, and K. Lee. Design of Side Cores of Injection Mold from Automatic Detection of Interference Faces. Journal of Design and Manufacturing, Vol. 3, No. 4, pp. 225-236, 1993.
• [34] T. Wong, S.T. Tan, and W.S. Sze. Parting line formation by slicing a 3D CAD model. Engineering with Computers, Vol. 14, No. 4, pp. 330-343, 1998.
• [35] X. G. Ye, J. Y. H. Fuh, and K. S. Lee. A hybrid method for recognition of undercut features from moulded parts. Computer Aided Design, Vol. 33, No. 14, pp. 1023-1034, 2001.
• [36] X. G. Ye, J. Y. H. Fuh, and K. S. Lee. Automatic Undercut Feature Recognition for Side Core Design of Injection Molds. Journal of Mechanical Design, Vol. 126, pp. 519-526, 2004.
• [37] Z. Yin, H. Ding, and Y. Xiong. Virtual Prototyping of Mold Design: Geometric Mouldability Analysis for Near-net-shape Manufactured Parts by Feature Recognition and Geometric Reasoning. Computer Aided Design, Vol. 33, No. 2, pp. 137-154, 2001.

9. 저작권:

이 자료는 아시스 고팔 바네르지 (Ashis Gopal Banerjee) 와 사티안드라 K. 굽타 (Satyandra K. Gupta) 의 논문: Geometrical algorithms for automated design of side actions in injection moulding of complex parts 를 기반으로 합니다.
논문 출처: https://www.researchgate.net/publication/222301183

이 자료는 위 논문을 기반으로 요약되었으며, 상업적 목적으로 무단 사용하는 것을 금지합니다.
Copyright © 2025 CASTMAN. All rights reserved.