SPHを用いた高圧ダイカストプロセスのモデリング

この紹介論文は、「CSIRO Mathematical and Information Sciences, Victoria, Australia.」によって発行された論文「Modelling the High Pressure Die Casting Process Using SPH」に基づいています。

1. 概要:

• 論文名: Modelling the High Pressure Die Casting Process Using SPH
• 著者: Paul W. Cleary and Joseph Ha
• 発表年: 2011年 (10月)
• 掲載学術誌/学会: CRC for Cast Metals Manufacturing (CAST), CSIRO Mathematical and Information Sciences, Victoria, Australia.
• キーワード: 高圧ダイカスト (HPDC), SPH (Smoothed Particle Hydrodynamics), 数値モデリング, 流体流動, 金型充填, 熱伝達, 凝固, 自由表面流れ

2. 抄録:

本論文では、このCAST資金提供プロジェクトの過去4年間にわたるHPDCのSPHモデリングの進捗状況をレビューします。2次元の単純な金型の充填の初期の例は、流れパターンの複雑さ、特に自由表面挙動と分裂の役割を示しています。これらの単純な金型の充填における熱伝達の組み込みの影響、特に金型内部の熱境界条件の影響と金型自体への結合伝導モデリングの重要性が示されています。SPH予測の精度を実証するために、水アナログ実験を用いた2つの検証例が示されています。3Dへのモデリングの拡張と、複雑な3次元金型形状を表現するために使用される方法論について説明します。現実的な工業部品の充填をモデル化するためのこのSPHシステムの使用が提示されます。金型充填順序の重要性、および角部や緩やかに湾曲した表面からの流れの剥離の役割が示されています。表面の断片化の程度、液滴形成、およびボイドの強い過渡的な性質も示されています。最後に、実際の自動車用ピストンヘッドのランナー、ゲート、および金型の充填が示され、このような大規模計算に固有の困難について議論されます。

3. 緒言:

高圧ダイカスト（HPDC）は、特に自動車産業におけるトランスミッションハウジング、ピストンヘッド、ギアボックス部品などの大量生産、低コスト部品の製造にとって重要なプロセスです。このプロセスでは、液体金属（一般的にはアルミニウム合金）が高速（約50～100 m/s）かつ非常に高い圧力で複雑なゲートおよびランナーシステムを通って金型に射出されます。金型の幾何学的複雑さは、著しい自由表面の断片化を伴う強力な三次元流体流動をもたらします。最小限の巻き込みボイドを持つ均質な鋳造部品を形成するためには、金型の様々な部分が充填される順序とガス出口の位置が重要です。これは、ゲーティングシステムの設計と金型の幾何形状によって決定されます。

製品品質とプロセス生産性の両方の改善は、改良された金型設計を通じて達成できます。これには、金型充填のより効果的な制御と金型熱性能の開発が含まれます。数値シミュレーションは、さまざまな金型設計と充填プロセスの有効性を研究するための強力かつ費用効果の高い方法を提供します。

4. 研究の概要:

研究トピックの背景:

HPDCは、溶融金属を高速・高圧で複雑な金型に射出することを特徴とする重要な工業プロセスです。複雑な流動パターン、自由表面の断片化、およびボイド巻き込みの可能性は、高品質な鋳物の実現に大きな課題をもたらします。金型充填プロセスを理解し制御することは、欠陥を最小限に抑えるために不可欠です。

先行研究の状況:

界面流をモデル化するためのオイラー法として、マーカーアンドセル（MAC）法やVOF（Volume of Fluid）法が用いられてきました。これらの手法の基本的な背景は、HwangとStoehr（1988）によるASM Metals HandbookやKotheら（1998）によって提示されています。VOF法は、MAGMAsoftやFlow-3Dなどのいくつかの商用ソフトウェアパッケージで使用されており、依然として金型充填シミュレーションで最も一般的で広く使用されている方法です。しかし、これらの手法は、複雑な界面現象の断片化や合体、数値拡散に課題を抱えることがあります。SPH（Smoothed Particle Hydrodynamics）は、流体を表現するために粒子のみを使用する特殊な数値手法であり、HPDCで見られるような液滴形成、飛沫、複雑な自由表面運動を伴う流体流動に特に適しています。SPHは、複雑な自由表面や材料界面の挙動（断片化を含む）を容易かつ自然にモデル化でき、ラグランジュフレームワークは運動量支配の流れを非常によく処理し、多相、状態方程式、凝固などの複雑な物理現象を容易に実装できるという利点があります。Clearyら（2000）およびHaとCleary（2000）による最近の研究では、2次元における高圧ダイカストへのSPHの適用と、これらのSPH結果と水アナログ実験との良好な比較が報告されています。

研究の目的:

本稿では、SPHを用いた高圧ダイカストプロセスのモデリングにおいてなされた進捗をレビューし、実際のHPDC例における詳細な流体流動のシミュレーションに関する新しい結果を提示します。

核心研究:

本研究は、HPDCシミュレーションのためのSPH法の適用と開発に焦点を当てています。これには以下が含まれます。

• SPH方法論: 連続方程式、運動量方程式、エネルギー方程式、状態方程式などのSPH支配方程式、および境界条件と数値実装の側面を詳述します。
• 2次元数値研究: 単純な金型形状（長方形、C字型）の等温充填をシミュレーションし、流動パターン、自由表面挙動、断片化、および金型、ゲート、またはランナー形状の変更の影響を理解します。
• 検証: コア付き円形ディスクおよびS字型キャビティに関する水アナログ実験と2D SPHシミュレーション結果を比較し、SPH予測の精度を評価します。
• 熱伝達と凝固の組み込み: C字型金型の充填プロセスにおける熱伝達、温度依存粘性、熱境界条件（等温対結合金型伝導）、および潜熱放出の影響を調査します。
• 3Dモデリング: 複雑な3D工業部品（汎用部品および実際の自動車用ピストンヘッド）における等温流のSPHによるモデリングを実証し、流れの剥離、断片化、および充填順序を強調します。

5. 研究方法論

研究設計:

本研究では、流体流動をシミュレーションするための特殊な数値手法であるSPH（Smoothed Particle Hydrodynamics）を採用しています。SPHは、流体を表現するために粒子のみを使用し、これらは流体方程式が解かれる計算フレームワークです。SPHは複雑な流れを自動的に追跡し、HPDCで見られるような液滴形成、飛沫、複雑な自由表面運動を伴う流体流動に特に適しています。材料は固定グリッドやメッシュではなく、自由に動き回る粒子によって近似されます。支配的な偏微分方程式は、これらの粒子の運動方程式に変換されます。

データ収集および分析方法:

SPHの定式化には以下が含まれます。

• 連続方程式: dρa/dt = Σb mb(va - vb) · ∇Wab (Equation 3)
• 運動量方程式: dva/dt = - Σb mb [(Pa/ρa²) + (Pb/ρb²) + Πab] ∇Wab + g (Equation 4の修正形式、ここでΠabは粘性項を含む: (ξ 4μaμb)/(ρaρb(μa+μb)) (vab·rab)/(rab²+η²))
• 状態方程式: P = P₀[ (ρ/ρ₀)γ - 1 ] (Equation 5), ここで P₀/ρ₀ = cs² = 100V² (Equation 6) および γ=7。
• エネルギー方程式 (エンタルピー形式): dHa/dt = Σb 4mb(kakb)/(ρaρb(ka+kb)) (Tab rab·∇Wab)/(rab²+η²) - Σb 2mb (ξμaμb)/(ρaρb(μa+μb)) ((vab·rab)² rab·∇Wab)/((rab²+η²)²) (Equation 7), ここで H = ∫cp(θ)dθ + L[1-fs(T)] (Equation 8)。
• 境界条件: 法線方向の境界力には反発的なレナード・ジョーンズポテンシャル力場を使用し、壁面での非滑り境界条件のためにはせん断力の総和に境界粒子を含めます。
• 近傍探索: 与えられた粒子の近傍粒子を特定するために、リンクリストを用いた探索グリッドを使用します。
• 3Dにおける初期設定: 鋳造部品の幾何学的記述を3次元ソリッドCADモデルの形で取得し、これを商用メッシュジェネレータへの入力として使用してメッシュを生成し、社内プリプロセッサを使用してSPH粒子用の初期設定に変換します。

様々なシナリオでシミュレーションが実施され、結果は速度、温度、または粘性によって色分けされた粒子プロット、および3D流れの場合はレンダリングされた表面メッシュを通じて可視化されました。検証のため、SPHの結果は水アナログ実験の実験データと比較されました。

研究トピックと範囲:

本研究はHPDCモデリングのいくつかの側面をカバーしています。

1. 2次元等温金型充填:
   • 単純な金型（短い長方形、長い長方形、インサート付きC字型金型）の充填により、流れパターン、ジェット挙動、断片化、およびボイド形成を研究。レイノルズ数（Re）500および2,500を使用。
   • C字型金型、ゲート、またはランナー形状の変更（反転ショットスリーブ、対称ショットスリーブ、金型キャビティへのくさび形インレット）が充填パターンに及ぼす影響。
2. 検証:
   • SchmidとKlein（1995、1998）による水アナログ実験とSPHシミュレーションの比較：
     • コア付き円形ディスク（金型厚さ2 mm、ゲート速度18.0 m/s）。
     • S字型キャビティ（金型厚さ2 mm、ゲート速度8.7 m/s）。
3. 熱伝達と凝固の組み込み:
   • 熱伝達を伴うC字型金型の充填モデリング。温度依存粘性モデル（Thomas方程式：μ= 4.5×10⁻⁶ ρm (1 + 2.5 fs + 10.05 fs² + 0.000273 exp(16.6fs))）を使用。
   • 熱境界条件の影響調査（27°Cの等温金型壁 対 外部温度350°Cの鋼製金型壁における結合熱伝導）。
   • 潜熱放出の影響評価（Al-1Cu-10Si合金の場合495 kJ/kg）。
4. 3次元等温流モデリング:
   • 汎用工業部品（円筒穴を持つスロット付き環状延長部、長さ約200 mm、粒子数292,931個、Re=27,875、ゲート速度44 m/s）の充填。
   • 実際の自動車用ピストンヘッド（円筒対称の上部、複雑な下部、幅3 mm×長さ38 mmのゲート）の充填。

6. 主な結果:

主な結果:

• 2次元等温充填:
  • SPHシミュレーションは、単純な2次元金型においても、ジェッティング、角部からの流れの剥離、自由表面の断片化、液滴形成などの複雑な流れパターンを実証しました。
  • 充填順序は金型形状に強く依存し、薄肉部では逆充填が一般的でした。
  • ランナー形状は、ゲートにおける流体速度プロファイルとその後の金型充填に大きな影響を与えます。
  • ゲート/ランナー設計の変更（例：反転ショットスリーブ、くさび形インレット）は、流体の分布にわずかな影響を与える可能性があり、流入が容易になるほど流れは広がり、初期領域の充填が不完全になる可能性があります。
• 検証:
  • SPHシミュレーションは、コア付き円形ディスクとS字型キャビティの両方について、水アナログ実験と良好な一致を示し、流れの微細な詳細、ジェット形状、ボイド形成、および全体的な充填パターンを捉えました。
• 熱伝達と凝固:
  • 熱伝達と凝固を含めると、等温の場合と比較して充填パターンが大幅に変化します。金型壁近くの凝固材料は、自由流動ジェットを金型中心に向かって押し出す可能性があります。
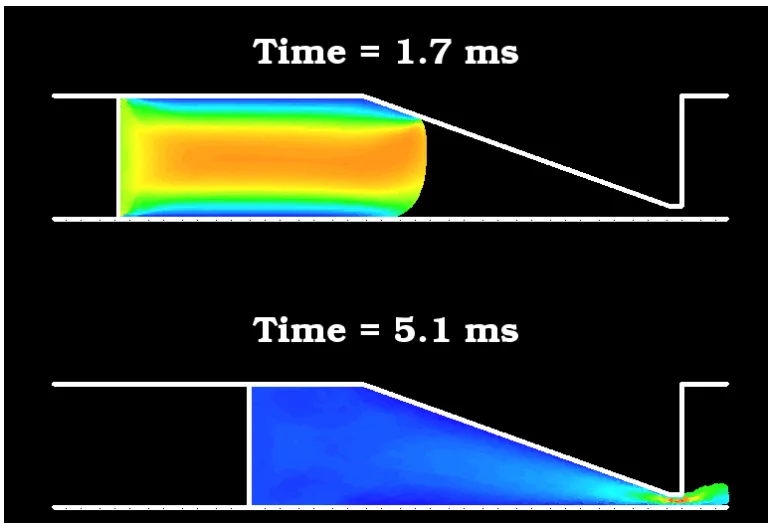
  • 等温金型境界条件は過剰な熱を除去し、早期凝固（湯境）を引き起こすため、金型への結合熱伝導のモデリングが不可欠です。現実的な金型の熱特性は、冷却速度と凝固速度を制限します。
  • 潜熱放出は、予測される凝固量を減らし、マッシーゾーン（固液共存領域）を狭め、自由流において凝固粒子の「スラリー」を形成する可能性があります。
• 3次元等温流:
  • SPHは複雑な3次元金型充填を成功裏にモデル化し、著しい流れの剥離、自由表面の断片化、および過渡的なボイド形成を示しました。
  • 3次元部品の充填順序は複雑であり、必ずしもゲートへの近接性に基づいていません。
  • 金型内部の「仮想カメラ」を用いた可視化は、局所的な流れ挙動に関する詳細な洞察を提供しました。
  • 汎用部品および自動車用ピストンヘッドのシミュレーションは、多数の粒子数の管理や微細な幾何学的特徴の解像といった課題を浮き彫りにしながら、産業的に関連のある大規模問題を処理するSPHの能力を実証しました。

図のリスト:

• Figure 1: View of the shot sleeve and piston used to accelerate the metal through the gate and into the die.
• Figure 2: Filling of a short rectangular die for Re=500.
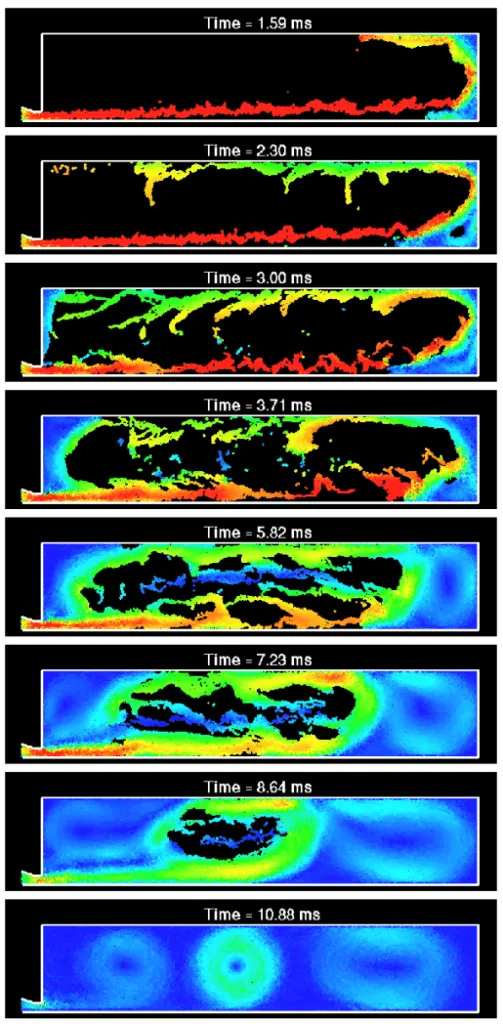
• Figure 3: Filling of a long rectangular die for Re=500.
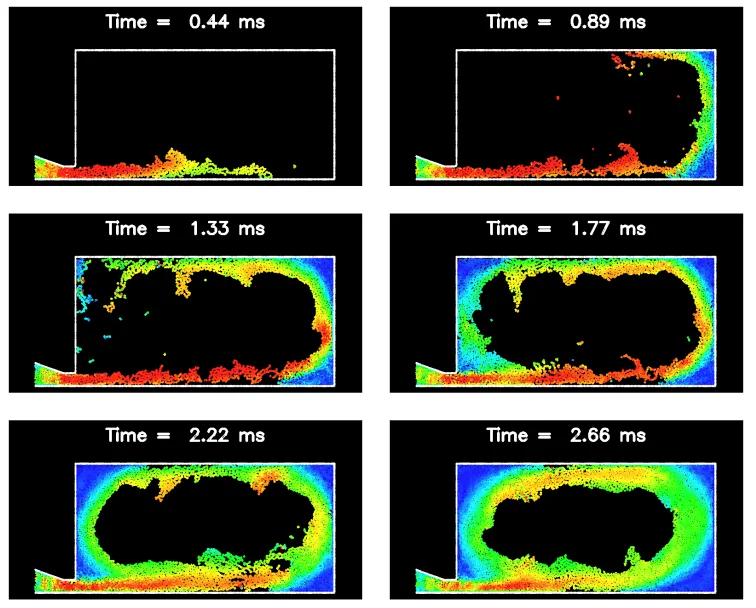
• Figure 4: Filling of C shaped die with insert for Re=2500
• Figure 5: Fill patterns for a C shaped die with different gates at time 0.50 ms.
• Figure 6: Fill patterns for a C shaped die with different gates at time 1.50 ms.
• Figure 7: Fill patterns for a C shaped die with different gates at time 3.00 ms.
• Figure 8: Filling of the circular die with a solid core using μ= 0.001 kg/ms
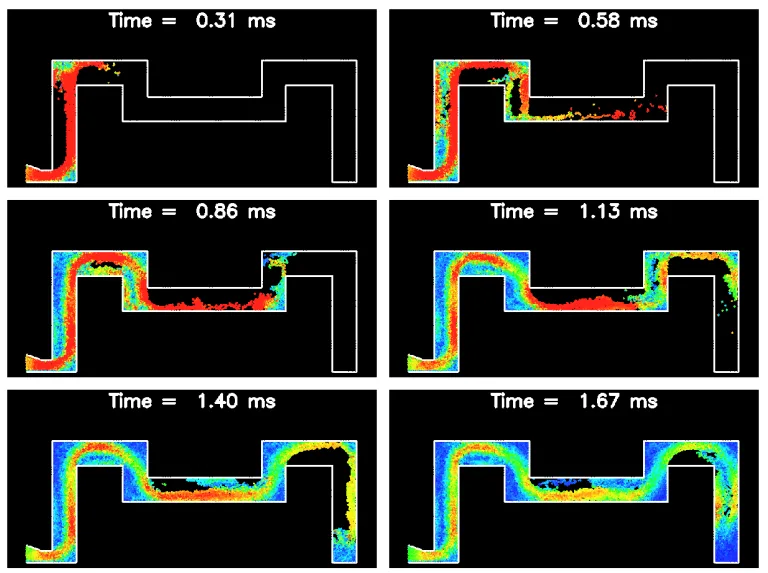
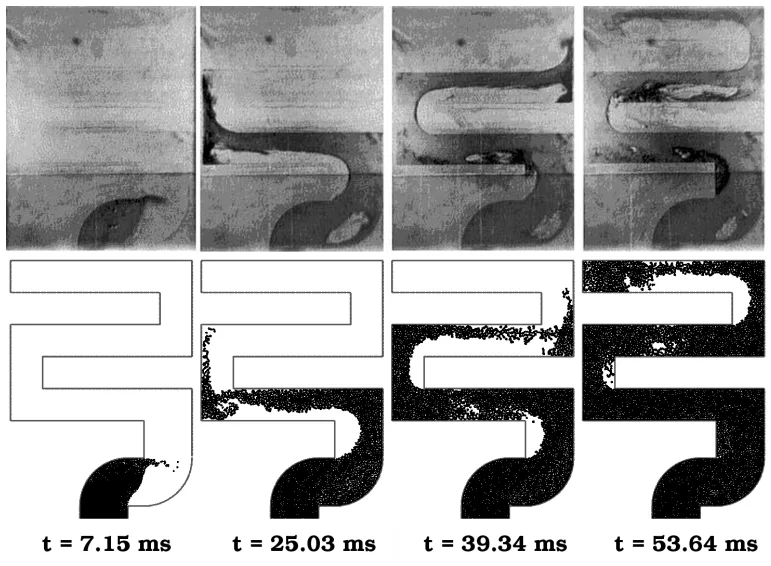
• Figure 9: Filling of the S shaped die using μ= 0.001 kg/ms
• Figure 10: (a) Original input viscosity data versus (b) modified viscosity temperature relation used in the SPH simulations with a finite value of μ below T₀ representing solidified metal.
• Figure 11: Temperature distribution in the liquid metal during the filling of an isothermal C shaped die for μs/μl=100. Light grey corresponds to hot metal above the liquidus temperature and dark grey to colder metal.
• Figure 12: Viscosity distribution in the liquid metal during the filling of an isothermal C shaped die for μs/μl=100. Dark grey corresponds to low viscosity and shows liquid metal while light grey corresponds to high viscosity and represents solid metal.
• Figure 13: Viscosity distribution when the conduction in the mould is also simulated.
• Figure 14: Viscosity distribution when the conduction in the mould is also simulated and latent heat is included.
• Figure 15: Geometry of the generic 3D HPDC component.
• Figure 16: Isothermal SPH simulation of the filling of the generic component.
• Figure 17: Two perspective views of the final filled die at 14 ms.
• Figure 18: Two internal views of the filling of the generic component.
• Figure 19: Geometry of the piston head, runner and venting system.
• Figure 20: Oblique upper view of the filling of the piston head.
• Figure 21: Side view of the filling of the piston head.

7. 結論:

SPH（Smoothed Particle Hydrodynamics）を用いた高圧ダイカストプロセスのモデリングに関するいくつかの側面が記述されました。非常に単純な形状の2次元等温モデリングは、充填が均一な前面充填ではないことを示しました。充填順序は金型形状に強く依存し、薄肉部の多くは逆充填によって充填されることがわかりました。角部からの流れの剥離は、気孔形成の重要な機会を提供します。数値シミュレーションにより、ゲートおよびランナー形状の変更が充填パターンに及ぼす影響を容易に検討できることが実証されました。

温度依存粘性を介した熱伝達と凝固の組み込みについて説明しました。金型壁の熱境界条件の選択の重要性は特に重要であり、これが冷却速度、ひいては凝固速度を制限するため、金型への結合伝導をモデル化する必要性が明確に示されました。潜熱放出が予測される凝固量を減らし、マッシーゾーンを狭め、自由流中に固体金属のスラリーを形成させる役割について検討しました。

最後に、SPHパッケージを使用して、2つの実際の複雑な形状の部品を3次元でモデル化することが実証されました。いずれの場合も、流れの剥離と自由表面の著しい断片化が、大きな過渡的なボイド形成につながりました。これらのより複雑な部品について、金型の充填順序の重要性が確認されました。

8. 参考文献:

• Cleary, P.W. (1998a). SPH Technical Note #29, CSIRO Division of Mathematical and Information Sciences, Technical Report CMIS 1998/166.
• Cleary, P.W. (1998b). Applied Mathematical Modelling, 22, 981–993.
• Cleary, P.W., Ha, J., & Ahuja, V. (2000). Int. J. Cast Metals Res, 12, 335–355.
• Cleary, P.W., Ha, J., Mooney, J., & Ahuja, V. (1998). in Proc. Proc. 13th Australasian Fluid Mechanics Conference, Melbourne, Australia, 679–682.
• Cleary, P.W. & Monaghan, J. J. (1999). J. Comp. Phys., 148, 227–264.
• Cleary, P.W., Sawley, M., and Ha, J. (2001). in Proc. 5th International Workshop on Bifurcation and Localisation in Soils and Rock, Balkema.
• Gartling, D.K. (1980). in Morgan, K., Taylor, C. and Brebbia, C.A. (Eds), Computer Methods in Fluids, Pentech, London, 257-284.
• Ha, J., Cleary, P.W., Alguine, V. and Nguyen, T. (1999). in Proc. 2nd Int. Conf. on CFD in Minerals & Process Industries, Melbourne, Australia, 423-428.
• Ha, J. and Cleary, P.W. (2000). SPH Technical Note #28, CSIRO Division of Mathematical and Information Sciences, Technical Report CMIS 2000/105.
• Ha, J. and Cleary, P.W. (2000). Int. J. Cast Metals Res, 12, 409–418.
• Ha, J., Schuhmann, R., Alguine, V., Cleary, P.W. and Nguyen, T. (2000). in Proc. Modeling of Casting, Welding and Advanced Solidification Processes IX, 151–158.
• Hirt, C.W. and Nichols, B.D. (1981). J. Comp. Phys., 39, 201–225.
• Hwang, W-S, and Stoehr, R.A. (1988). Metals Handbook, Casting ASM International, 15, 867-876.
• Jai, L.R., Xiong, S.M. and Lui, B.C. (1998) in Proc. Modeling of Casting, Welding and Advanced Solidification Processes IX, Aachen, Germany, 303–310.
• Kothe, D., Brackbill, J.U. and Choi, C.K. (1990). Physics of Fluids B, 2, 1898–1906.
• Kothe, D., Juric, D., Lam, K. and Lally, B. (1998). in Proc. Modeling of Casting, Welding and Advanced Solidification Processes VIII, San Diego, California, 17–28.
• Lee, Y.C., Hwang, H.Y. and Choi, J.K. (2000). in Proc. Modeling of Casting, Welding and Advanced Solidification Processes IX, Aachen, Germany, 349–356.
• Monaghan, J. J. (1992). Ann. Rev. Astron. Astrophys., 30, 543.
• Monaghan, J. J. (1994). J. Comp. Phys., 110, 399–406.
• Morris, J.P. (2000). Int. J. Numer. Methods Fluids, 33, 333-353.
• Scheppe, F., Sahm, P.R., Hermann, W., Paul, U. and Preuhs, J. (2000). in Proc. Modeling of Casting, Welding and Advanced Solidification Processes IX, Aachen, Germany, 207–214.
• Schmid, M., and Klein F. (1995). in Proc. NADCA 18. International Die Casting Congress and Exposition, October 2-5, 1995, Indianapolis, Indiana, Paper No.I-T95-034, 93-99.
• Schmid, M. (1998). (Private Communication),
• Schmid, M. and Klein, F. (1998). in Proc. Modeling of Casting, Welding and Advanced Solidification Processes VIII, San Diego, California, 1131–1136.
• Schneider, M.C., Beckermann, C., Lipinski, D.M. and Schaefer, W. (2000). in Proc. Modeling of Casting, Welding and Advanced Solidification Processes IX, Aachen, Germany, 257–264.
• Thomas (1965). J. Colloid Science, 20, 267–277.
• Voller, V.R. and Prakash, C. (1987). Int. J. Heat Mass Transfer, 30, 1709–1719.
• Welch, J.E. and Harlow, F.H. (1966). Physics of Fluids, 9, 842-851.
• Xu, Z.A. (2000). in Proc. Modeling of Casting, Welding and Advanced Solidification Processes IX, Aachen, Germany, 312–319.

9. 著作権:

• この資料は、「Paul W. Cleary and Joseph Ha」による論文です。「Modelling the High Pressure Die Casting Process Using SPH」に基づいています。
• 論文の出典: https://www.researchgate.net/publication/246854585

この資料は上記の論文に基づいて要約されており、商業目的での無断使用は禁止されています。
Copyright © 2025 CASTMAN. All rights reserved.