AN OVERVIEW OF HEAT SINK TECHNOLOGY

この論文の要約は、[Int. J. of Applied Mechanics and Engineering (IJME)]で発表された論文「[AN OVERVIEW OF HEAT SINK TECHNOLOGY]」に基づいています。

1. 概要:

  • タイトル: AN OVERVIEW OF HEAT SINK TECHNOLOGY
  • 著者: Ehsan F. Abbas
  • 出版年: 2024年
  • 出版ジャーナル/学会: Int. J. of Applied Mechanics and Engineering (IJME)
  • キーワード: heat sink design, longitudinal fin, performance of a heat sink, improving fin performance, fin optimization.
Fig.1. Illustrations of heat sink samples according to the manufacturing method.
Fig.1. Illustrations of heat sink samples according to the manufacturing method.

2. 研究背景:

  • 研究トピックの社会的/学術的背景:
    本研究は、電気・電子機器、化学産業、冷凍、空調システム、発電所など、様々な用途における熱エネルギー管理において、ヒートシンクが重要な役割を果たしていることに焦点を当てています。論文では、初期の鋳鉄製設計から現代的なソリューションに至るまでのヒートシンク技術の歴史的発展を概説し、産業および家庭環境における効率的な熱管理に対する需要の高まりが、その進化を牽引してきたことを強調しています。この背景は、産業革命の進展と生活水準の向上を背景としており、より洗練された効率的なヒートシンク設計の必要性を生み出しています。
  • 既存研究の限界:
    論文の序論では、既存研究の限界は明示的には詳述されていませんが、特に縦型長方形フィンに焦点を当てたヒートシンク技術の包括的な概要の必要性が暗黙のうちに示唆されています。歴史的レビューは、ヒートシンク技術が進化してきた一方で、設計原則の最適化と理解が継続的に必要であることを示唆しています。論文は、進歩にもかかわらず、特にフィン設計と構成に関して、最適なヒートシンク性能を達成するには課題が残っていることを指摘しています。
  • 研究の必要性:
    本研究は、ヒートシンク技術の構造化された概要を提供するために必要であり、特に縦型長方形フィンの設計と最適化に焦点を当てています。論文は、様々なデバイスの信頼性と性能にとって効率的な放熱が重要であることを強調しています。歴史的発展、製造方法、冷却方法、設計パラメータ、最適化技術をレビューすることにより、論文は知識を統合し、この分野のエンジニアや研究者にとって貴重なリソースを提供することを目指しています。縦型長方形フィンに焦点を当てることは、その一般的な使用法と、最適化のための広範な研究データが入手可能であることによって正当化されます。

3. 研究目的と研究課題:

  • 研究目的:
    本研究の主な目的は、ヒートシンク技術の概要を提供することであり、特に強制対流および自然対流を受けるアレイにおける縦型長方形フィンの最適化に焦点を当てています。論文は、ヒートシンク技術の発展を振り返り、縦型長方形フィンの基本原理と最適化技術を統合することを目指しています。
  • 主な研究課題:
    明示的に課題として述べられてはいませんが、本研究は暗黙のうちに以下の点に取り組んでいます。
    • ヒートシンク技術はどのように進化してきたか？
    • ヒートシンクの様々な製造方法とその影響は？
    • ヒートシンク技術で採用されている様々な冷却方法は？
    • ヒートシンク設計における主要な設計パラメータと仮定は？
    • 特に縦型長方形フィンに関して、ヒートシンクを設計および最適化するための理論的アプローチは？
    • フィン効率と有効性はどのように評価および最適化できるか？
    • 様々な条件下での異なるフィンプロファイルの最適寸法は？
    • 多フィンアレイの熱抵抗はどのように分析できるか？
    • ヒートシンク性能に関する実験的および数値的研究からの知見は？
  • 研究仮説:
    この論文は概要であり、特定の仮説を検証するものではありません。しかし、既存の文献の包括的なレビューが、特に縦型長方形フィンに関して、ヒートシンクの設計と最適化のための貴重な洞察とガイドラインを提供できるという暗黙の前提に基づいています。論文は、既存の知識を統合して、この分野の構造化された理解を提示しています。

4. 研究方法

  • 研究デザイン:
    文献レビュー。この論文は、ヒートシンク技術、特に縦型長方形フィンに焦点を当てた既存の研究と知識を統合したレビュー論文です。
  • データ収集方法:
    データ収集方法は、ヒートシンク技術に関連する研究論文、書籍、技術レポートなどの公開文献の包括的なレビューを含みます。論文の最後にリストされている参考文献が情報源を示しています。
  • 分析方法:
    分析方法は質的であり、レビューされた文献からの情報を要約、統合、および整理することを含みます。論文は、歴史的発展、製造方法、冷却方法、設計パラメータ、理論モデル、最適化技術、実験的/数値的知見など、ヒートシンク技術の様々な側面に関する構造化された概要を提示しています。引用された文献からの数式と図は、主要な概念と結果を説明するために使用されています。
  • 研究対象と範囲:
    研究対象はヒートシンク技術であり、特に縦型長方形フィンに焦点を当てています。レビューは、ヒートシンクの設計、最適化、および性能評価の様々な側面を網羅しており、この分野の幅広い研究に基づいています。範囲は主に、ヒートシンク、特に縦型長方形フィン構成の熱伝達に関連する理論的および実験的研究に焦点を当てています。

5. 主な研究成果:

  • 主な研究成果:
    • 歴史的発展: 論文は、20世紀初頭の多柱式鋳鉄設計から現代の材料と製造技術に至るまでのヒートシンクの進化をたどり、社会的および産業の変化によって推進された主要なマイルストーンと設計優先順位の変化を強調しています。
    • 製造方法: レビューでは、スタンピング、押し出し、接合フィン、鋳造、溶接フィンなど、ヒートシンクの様々な製造方法を概説し、それぞれの利点、限界、および用途を詳述しています。図1は、製造方法によるヒートシンクのサンプルを示しています。
    • 冷却方法: 論文は、受動型、能動型、準能動型、液冷プレート型、および相変化再循環システムへの冷却方法を分類し、各方法の動作原理と一般的な用途を説明しています。図2は、冷却方法によるヒートシンクのサンプルの図を示しています。
    • 設計パラメータと仮定: ヒートシンクの主要な設計パラメータは、流速、圧力損失、断面積、熱伝達要件、動作温度、サイズ制限、重力方向、外観、およびコストなどとして特定されています。簡略化された分析のためにヒートシンク設計で行われた仮定もリストされており、放射熱伝達の無視や均一なベース温度などが含まれます。
    • 設計への理論的アプローチ: 論文は、縦型長方形フィンに焦点を当てて、ヒートシンクを設計するための理論的枠組みを提示しています。温度分布方程式（図3）、異なるフィン先端条件に対する熱伝達方程式（表1および2）、フィン効率と有効性の式を提供しています。
    • フィン最適化: レビューでは、修正プロファイル長、フィン有効性、および一定熱流束および一定体積条件下でのフィン厚さと長さを最適化する方法を含むフィン最適化技術について説明しています。最適なフィン寸法の式が提示されています。
    • 多フィンアレイの熱抵抗: 論文は、多フィンアレイの熱抵抗を分析し、熱伝達率と全体的な表面効率を計算するための式を提供しています（図4）。
    • 非均一プロファイル面積を持つ縦型フィン: レビューは、非均一プロファイル（三角形、凹面、凸面）を持つ縦型フィンにまで拡張され、これらのフィン形状の最適な寸法方程式と熱伝達方程式を提示しています（図5および表3）。
    • 縦型フィンアレイ: 論文では、自然層流対流のためのフィンアレイにおける平行な垂直プレート間の間隔の最適化について説明し、熱伝達率とアレイ設計のための最適なパラメータの方程式を提示しています（図6および7）。
    • 実験的および数値的研究: レビューでは、フィン形状、間隔、方向、および流れ条件の影響など、ヒートシンク性能の様々な側面を調査した多数の実験的および数値的研究からの知見を要約しています。図8は、従来のヒートシンクモデルとハイブリッドヒートシンクモデルを示し、図9は、研究されたヒートシンクモデルを示しています。
  • 統計的/質的分析結果:
    論文は主に、様々な研究からの質的な知見を統合しています。定量的な結果は、熱伝達率、フィン効率、最適寸法、および熱抵抗の形式の方程式と式で示されています。レビューは、フィン間隔が熱伝達係数に与える影響、中断フィンの有効性、および異なるフィン形状の性能など、実験的および数値的研究からの傾向と一般的な結論を強調しています。
  • データ解釈:
    論文で提示および統合されたデータは、ヒートシンク、特に縦型長方形フィンの設計と最適化が、多数のパラメータと考慮事項を含む複雑なプロセスであることを示しています。最適な設計は、用途、冷却方法、材料特性、および環境条件などの様々な要因に依存します。レビューは、効率的なヒートシンク設計を達成するために、理論モデリング、数値シミュレーション、および実験的検証の重要性を強調しています。
  • 図の名前リスト:
    • Fig. 1. 製造方法によるヒートシンクのサンプル図。
    • Fig. 2. 冷却方法によるヒートシンクのサンプル図。
    • Fig. 3. 長方形断面の縦型フィン [8]。
    • Fig. 4. 平面壁を備えたフィンを組み合わせた熱損失のスケッチ。
    • Fig. 5. 非均一プロファイル面積を持つ縦型フィンのスケッチ：（a）三角形、（b）凹面、（c）凸面 [9]。
    • Fig. 6. 縦型フィンアレイとその幾何学的定義のスケッチ [9]、[18]。
    • Fig. 7. 任意の縦型フィンアレイの最適なβ値 [9]、[18]。
    • Fig. 8. 2つのヒートシンクモデルのスケッチ：（a）従来型、（b）ハイブリッド。
    • Fig. 9. 研究されたヒートシンクモデルのスケッチ、（a）ストレートフィン、（b）トポロジー。
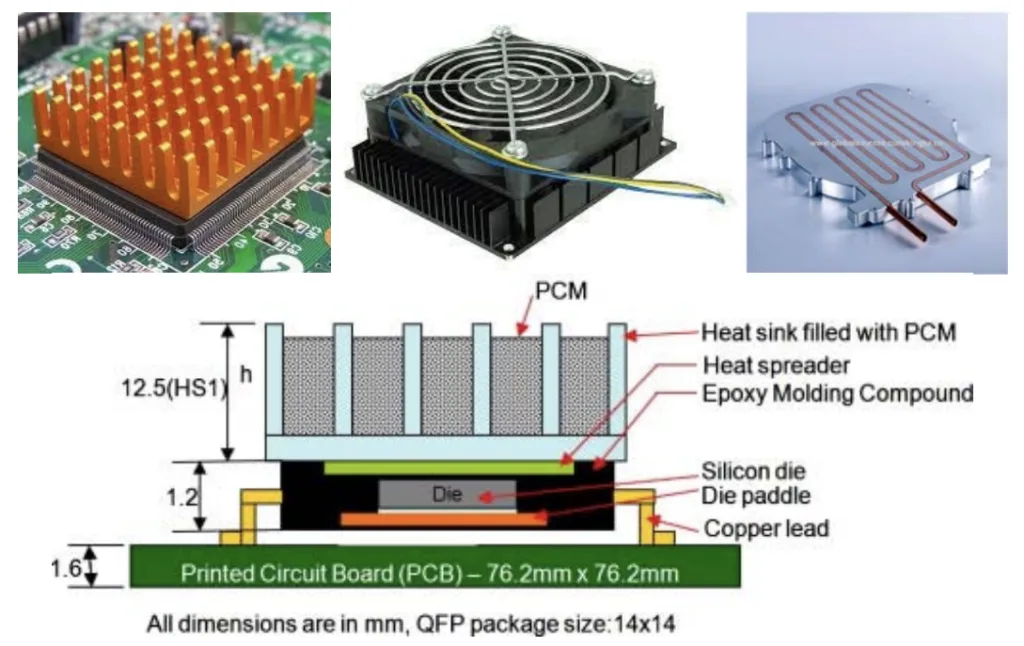
Fig.9. Sketch of studied heat sink models, (a) straight fin, (b) topology.
Fig.9. Sketch of studied heat sink models, (a) straight fin, (b) topology.

6. 結論と考察:

  • 主な結果の要約:
    この概要論文は、長方形縦型フィンを備えたヒートシンクの設計最適化が、過去数世紀にわたって広範囲に研究されてきたと結論付けています。最適な構成を決定するために、様々な実験的、数値的、および理論的方法が採用されてきました。主な知見は、フィン高さと間隔が熱伝達率に大きな影響を与え、最適なフィン間隔が熱伝達を最大化するために重要であるということです。デュラルミンフィンは、同様の形状のステンレス鋼よりも優れた性能を発揮します。中断フィンと傾斜フィン、および長方形ノッチフィンなどの特定のフィン形状は、熱伝達性能を向上させることができます。
  • 研究の学術的意義:
    このレビュー論文は、ヒートシンク技術、特に縦型長方形フィンに関する幅広い研究知見を統合することにより、貴重な学術的貢献を提供しています。歴史的発展、設計原則、最適化技術、および実験結果の構造化された概要を提供し、熱工学の研究者や学生にとって包括的なリソースとして役立ちます。論文は、ヒートシンク設計の進化と性能に影響を与える主要な要因を強調しています。
  • 実用的な意義:
    本研究の実用的な意義は、様々な産業における熱管理に関与するエンジニアや設計者にとって重要です。論文は、様々な用途や冷却条件に合わせてヒートシンクを設計および最適化するためのガイドラインと式を提供しています。要約された知見は、電子機器、電力システム、およびその他の熱応用において、効率的で費用対効果の高い放熱を達成するために、適切な製造方法、冷却戦略、フィン形状、および材料を選択するのに役立ちます。最適なフィン間隔の強調と、中断フィンおよび傾斜フィンの性能上の利点は、実用的な設計改善のための実行可能な洞察を提供します。
  • 研究の限界:
    レビュー論文として、限界はレビューされた文献の範囲に内在しています。論文は広範な概要を提供していますが、ヒートシンク技術のすべての研究や側面を網羅的に詳細にカバーしているわけではありません。焦点は主に縦型長方形フィンであり、他のフィン構成や高度なヒートシンク技術はそれほど広範囲にカバーされていない可能性があります。レビューは、含まれる研究の選択によっても制限されており、一般的な研究分野への偏りを反映している可能性があります。

7. 今後のフォローアップ研究:

  • フォローアップ研究の方向性:
    論文は暗黙のうちに、今後の研究のためのいくつかの方向性を示唆しています。
    • 従来の設計を超えて熱伝達性能を向上させるための、高度なヒートシンク形状と材料のさらなる調査。
    • 複雑で最適化されたフィン構造の製造を可能にするための、新しい製造技術の探求。
    • 効率と適応性を向上させるための、受動冷却戦略と能動冷却戦略を組み合わせたハイブリッド冷却方法に関するさらなる研究。
    • 最適化されたヒートシンクの長期的な信頼性と、実際の動作条件下での性能に関するより深い研究。
    • 高電力密度エレクトロニクスや持続可能なエネルギーシステムなど、特定の熱管理課題を抱える新たな用途向けのヒートシンク設計の調査。
    • 特に複雑なフィン形状と流れ条件において、既存の理論モデルと数値シミュレーションを、より包括的な実験データで改良および検証するためのさらなる研究。
  • さらなる探求が必要な分野:
    • スペースの制約、重量制限、費用対効果などの要因を考慮した、特定の用途および環境条件に対するヒートシンクの最適化。
    • 複雑な流れ領域下でのヒートシンク性能を予測するための、より正確で計算効率の高い数値モデルの開発。
    • 製造公差と表面仕上げがヒートシンクの実際の熱性能に与える影響の調査。
    • 包括的な熱ソリューションのために、システムレベルの熱管理戦略と統合された革新的なヒートシンク設計の探求。

8. 参考文献:

  • [1] Kordyban T. (1998): Hot Air Rises and Heat Sinks: Everything You Know About Cooling Electronics Is Wrong.- ASME Press, p.236, https://doi.org/10.1115/1.800741.
  • [2] Lee S. (1995): Optimum design and selection of heat sinks.– IEEE Transactions on Components, Packaging, and Manufacturing Technology: Part A, vol.18, No.4, pp. 812-817, doi: 10.1109/95.477468.
  • [3] Londhe K. and Kaushik V.R. (2017): Heat sink design for optimal performance of compact electronic appliances - a review.- Journal for Advanced Research in Applied Sciences, vol.4, No.5, pp.13-21.
  • [4] Kandasamy R., Wang X.Q. and Mujumdar A.S. (2008): Transient cooling of electronics using phase change material (PCM)-based heat sinks.- Appl. Therm. Eng., vol.28, No.8-9, pp.1047-1057, doi: 10.1016/J.APPLTHERMALENG.2007.06.010.
  • [5] Kays W.M. and London A.L. (2011): Compact Heat Exchangers.– Third Edition,
  • [6] https://celsiainc.com/technology/heat-sink-design/.
  • [7] Lee H.S. (2010): Thermal Design: Heat Sinks, Thermoelectrics, Heat Pipes, Compact Heat Exchangers, and Solar Cells.- John Wiley & Sons, Inc., doi: 10.1002/9780470949979.
  • [8] Holman J.P. (2010): Heat Transfer.– 10th ed., p.758, McGraw-Hill Education
  • [9] Kraus A.D., Aziz A. and Welty J. (2001): Extended Surface Heat Transfer.– A Wiley-Interscience Publication J.WILEY & SONS, Inc., doi: 10.1002/9780470172582.
  • [10] Cengel Y., Turner R. and Smith R. (2001): Fundamentals of thermal-fluid sciences.- Appl. Mech. Rev., vol.54, No.6, doi: 10.1115/1.1421126.
  • [11] Brown A. (1965): Optimum dimensions of uniform annular fins.– Int. J. Heat Mass Transf., vol.8, No.4, pp.655-662, doi: 10.1016/0017-9310(65)90051-7.
  • [12] Cobble M.H. (1971): Optimum fin shape.- J. Franklin Inst., vol.291, No.4, pp.283-292, doi: 10.1016/0016-0032(71)90184-0.
  • [13] Snider A.D. and Kraus A.D. (1987): The quest for the optimum longitudinal fin profile.– Heat Transfer Engineering, vol.8, No.2, doi: 10.1080/01457638708962790.
  • [14] Duffin R. (1959): A variational problem relating to cooling fins.- Indiana University Mathematics Journal, vol.8, No.1, doi: 10.1512/iumj.1959.8.58003.
  • [15] Maday C.J. (1974): The minimum weight one-dimensional straight cooling fin.– J. Eng. Ind., vol.96, No.1, pp.161-165, https://doi.org/10.1115/1.3438291 .
  • [16] Ernst E.R.G., Eckert R.G. and Drake R.M. (1987): Analysis of heat and mass transfer.- Hemisphere Pub. Corp., accessed: Nov. 21, 2023, [Online], available: https://inis.iaea.org/search/search.aspx?orig_q=RN:19100674
  • [17] Razelos P. and Imre K. (1983): Minimum mass convective fins with variable heat transfer coefficients.- J. Franklin Inst., vol.315, No.4, doi: 10.1016/0016-0032(83)90078-9.
  • [18] Aziz A. (1992): Optimum dimensions of extended surfaces operating in a convective environment.– Appl. Mech. Rev., vol.45, No.5, doi: 10.1115/1.3119754.
  • [19] Bergman T.L., Lavine A.S., Incropera F.P. and DeWitt D.P. (2015): Fundamentals of Heat and Mass Transfer.- John Wiley & Sons, USA.
  • [20] Chung B.T.F. and Iyer J.R. (1993): Optimum design of longitudinal rectangular fins and cylindrical spines with variable heat transfer coefficient.- Heat Transfer Engineering, vol.14, No.1, pp.31-41, doi: 10.1080/01457639308939792.
  • [21] Schmidt E. (1926): Die Wärmeübertragung Durch Rippen.
  • [22] Chung B.T.F. and Nguyen L.D. (1986): Optimization of design parameters for radiating longitudinal fins of various geometries.- in AIAA Paper, doi: 10.2514/6.1986-150.
  • [23] Levy E.K. (1971): Optimum plate spacings for laminar natural convection heat transfer from parallel vertical isothermal flat plates.– J. Heat Transfer, vol.93, No.4, pp.463-465, doi: 10.1115/1.3449847.
  • [24] Elenbaas W. (1942): Heat dissipation of parallel plates by free convection.- Physica, vol.9, No.1, pp.1-28, doi: 10.1016/S0031-8914(42)90053-3.
  • [25] Bodoia J.R. and Osterle J.F. (1962): The development of free convection between heated vertical plates.- J. Heat Transfer, vol.84, No.1, pp.40-43, doi: 10.1115/1.3684288.
  • [26] Bar-Cohen A. and Jelinek M. (1985): Optimum arrays of longitudinal, rectangular fins in corrective heat transfer.- Heat Transfer Engineering, vol.6, No.3, pp.68-78, doi: 10.1080/01457638508939633.
  • [27] Starner K.E. and McManus H.N. (1963): An experimental investigation of free-convection heat transfer from rectangular-fin arrays.- J. Heat Transfer, vol.85, No.3, pp.273-277, doi: 10.1115/1.3686097.
  • [28] Jones C.D. and Smith L.F. (1970): Optimum arrangement of rectangular fins on horizontal surfaces for free-convection heat transfer.- J. Heat Transfer, vol.92, No.1, doi: 10.1115/1.3449648.
  • [29] Barrett A.V. and Obinelo I.F. (1997): Characterization of longitudinal fin heat sink thermal performance and flow bypass effects through CFD methods.- in Annual IEEE Semiconductor Thermal Measurement and Management Symposium, doi: 10.1109/stherm.1997.566793.
  • [30] De Lieto Vollaro A., Grignaffini S. and Gugliermetti F. (1999): Optimum design of vertical rectangular fin arrays.- International Journal of Thermal Sciences, vol.38, No.6, pp. 525-529, doi: 10.1016/S1290-0729(99)80025-8.
  • [31] Baskaya S., Sivrioglu M. and Ozek M. (2000): Parametric study of natural convection heat transfer from horizontal rectangular fin arrays.– International Journal of Thermal Sciences, vol.39, No.8, pp.797-805, doi: 10.1016/S1290-0729(00)00271-4.
  • [32] Bar-Cohen A., Iyengar M. and Kraus A.D. (2003): Design of optimum plate-fin natural convective heat sinks.- Journal of Electronic Packaging, Transactions of the ASME, vol.125, No.2, pp.208-216, SPEC., doi: 10.1115/1.1568361.
  • [33] Yazicioğlu B. and Yüncü H. (2007): Optimum fin spacing of rectangular fins on a vertical base in free convection heat transfer.- Heat and Mass Transfer/Waerme- und Stoffuebertragung, vol.44, No.1, pp.11-21, doi: 10.1007/s00231-006-0207-6.
  • [34] Mittelman G., Dayan A., Dado-Turjeman K. and Ullmann A. (2007): Laminar free convection underneath a downward facing inclined hot fin array.- Int. J. Heat Mass Transf., vol.50, No.13-14, pp.2582-2589, doi: 10.1016/j.ijheatmasstransfer.2006.11.033.
  • [35] Shaeri M.R. and Yaghoubi M. (2009): Thermal enhancement from heat sinks by using perforated fins.– Energy Convers. Manag., vol.50, No.5, pp.1264-1270, doi: 10.1016/j.enconman.2009.01.021.
  • [36] Kim D.K. (2012): Thermal optimization of plate-fin heat sinks with fins of variable thickness under natural convection.- Int. J. Heat Mass Transf., vol.55, No.4, pp.752-761, doi: 10.1016/j.ijheatmasstransfer.2011.10.034.
  • [37] Ahmadi M., Mostafavi G. and Bahrami M. (2014): Natural convection from rectangular interrupted fins.- International Journal of Thermal Sciences, vol.82, No.1, pp.62-71, doi: 10.1016/j.ijthermalsci.2014.03.016.
  • [38] Pouryoussefi S. and Zhang Y. (2015): Experimental study of air-cooled parallel plate fin heat sinks with and without circular pin fins between the plate fins.- Journal of Applied Fluid Mechanics, vol.8, No.3, pp.515-520, doi: 10.18869/acadpub.jafm.67.222.22930.
  • [39] Karamanis G. and Hodes M. (2016): Longitudinal-fin heat sink optimization capturing conjugate effects under fully developed conditions.– J. Therm. Sci. Eng. Appl., vol.8, No.4, p.7, doi: 10.1115/1.4034339.
  • [40] Shadlaghani A., Tavakoli M.R., Farzaneh M. and Salimpour M.R. (2016): Optimization of triangular fins with/without longitudinal perforate for thermal performance enhancement.– Journal of Mechanical Science and Technology, vol.30, No.4, pp.1903-1910, doi: 10.1007/s12206-016-0349-5.
  • [41] Hong S.H. and Chung B.J. (2016): Variations of the optimal fin spacing according to Prandtl number in natural convection.- International Journal of Thermal Sciences, vol.101, pp.1-8, doi: 10.1016/J.IJTHERMALSCI.2015.10.026.
  • [42] Dogan M. and Dogan D. (2017): Experimental investigation of natural convection heat transfer from fin arrays for different tip-to-base fin spacing ratios.- Isi Bilimi Ve Teknigi Dergisi/ Journal of Thermal Science and Technology, vol.37, No.1, pp.147-157.
  • [43] Jaya Krishna D. (2018): Operational time and melt fraction based optimization of a phase change material longitudinal fin heat sink.– J. Therm. Sci. Eng. Appl., vol.10, No.6, p.4, doi: 10.1115/1.4040988.
  • [44] Hou D., Xin X. and Qian J. (2020): Analysis of natural convection heat transfer from vertical and inclined plate fin heat sinks.- in Lecture Notes in Electrical Engineering, Springer Verlag, pp.479-487, doi: 10.1007/978-981-32-9441-7_49.
  • [45] Jasim H.H. (2020): Heat transfer enhancement from heat sources using optimal design of combined fins heat-sinks.- Propulsion and Power Research, vol.9, No.4, pp.372-382, doi: 10.1016/j.jppr.2020.11.002.
  • [46] Xie L., Zhang Y., Ge M. and Zhao Y. (2022): Topology optimization of heat sink based on variable density method.– Energy Reports, vol.8, pp.718-726, doi: 10.1016/J.EGYR.2021.11.214.
  • [47] Obaid A.J. and Hameed V.M. (2023): An experimental and numerical comparison study on a heat sink thermal performance with new fin configuration under mixed convective conditions.– S. Afr. J. Chem. Eng., vol.44, pp.81-88, doi: 10.1016/J.SAJCE.2023.01.009.
  • [48] Kaya M. and Kaya Ş. (2023): Optimum fin spacing of rectangular fins on aluminum heat sinks plates.- Proceedings of the Romanian Academy Series A - Mathematics Physics Technical Sciences Information Science, vol.24, No.2, pp.157-157.

9. 著作権:

  • この資料は、「Ehsan F. Abbas」氏の論文：「AN OVERVIEW OF HEAT SINK TECHNOLOGY」に基づいています。
  • 論文ソース: https://doi.org/10.59441/ijame/192127

この資料は上記の論文に基づいて要約されたものであり、商業目的での無断使用は禁止されています。
Copyright © 2025 CASTMAN. All rights reserved.

PDF Downloads
Tags: Applications; ,CAD; ,CFD; ,Efficiency; ,Heat Sink; ,Review; ,해석