Multi-component topology optimization for die casting (MTO-D)

1. 概要:

  • タイトル: Multi-component topology optimization for die casting (MTO-D)
  • 著者: Hao Zhou, Junyuan Zhang, Yuqing Zhou, Kazuhiro Saitou
  • 出版年: 2019年
  • 掲載ジャーナル/学会: Structural and Multidisciplinary Optimization
  • キーワード: Multi-component topology optimization, Manufacturability, Die cast components, Parting lines

2. 研究背景:

  • 研究トピックの社会的/学術的背景:
    • トポロジー最適化は、革新的な設計ソリューションを生み出す効果的なツールとして広く採用されている。
    • しかし、現状では単一コンポーネント（モノリシック）構造の設計に主に使用されており、多くの工業製品は複数のコンポーネントからなるアセンブリである。
    • 複雑な形状は単一の部品として製造することが経済的に困難または不可能であるため、複雑な形状をより単純なコンポーネント形状に分割する必要がある。
    • 性能と製造コストのバランスを慎重に検討する必要がある。
    • 1990年代から、マルチコンポーネントアセンブリのトポロジー最適化の研究が行われてきた。
    • 従来の単一部品トポロジー最適化に基づく定式化は、複数コンポーネントからなる構造アセンブリへの適用を制限している。
  • 既存研究の限界:
    • 既存研究では、コンポーネントの境界を所与の入力として扱うか、コンポーネントの埋め込みの副産物として扱うことが多く、構造性能と製造コストのバランスの結果としてコンポーネント境界を最適化する研究は少ない。
    • 既存のマルチコンポーネントトポロジー最適化手法は、計算効率が課題であった。
    • トポロジー最適化は、製造プロセスによって課せられる幾何学的制約を無視することが多く、製造が困難な設計が生成される。
    • 最適化後の設計編集は、構造性能の点で準最適な設計になる可能性がある。
  • 研究の必要性:
    • 製造可能性を考慮したマルチコンポーネント構造の設計合成を実現する必要がある。
    • 鋳造プロセスにおける製造制約を考慮したトポロジー最適化手法の開発が求められている。
    • 特に、ダイカストプロセスに特化したマルチコンポーネントトポロジー最適化手法の開発が重要である。

3. 研究目的と研究課題:

  • 研究目的:
    • ダイカスト（MTO-D）プロセスで製造される構造アセンブリのためのマルチコンポーネントトポロジー最適化手法を提示すること。
    • 各部品が、金型抜き方向の完全密閉された空洞とアンダーカットがないことを保証する手法を開発すること。
  • 主要な研究課題:
    • ダイカストプロセスにおける製造制約を組み込んだマルチコンポーネントトポロジー最適化の数学的定式化。
    • 各コンポーネントの抜き勾配と密閉空洞の制約を効率的にモデル化し、最適化に組み込む方法。
    • 最適化された設計が、抜き方向のアンダーカットがなく、完全に密閉された空洞がないことを数値的に検証すること。
  • 研究仮説:
    • 提案手法を用いることで、ダイカストプロセスで製造可能なマルチコンポーネント構造のトポロジー最適化設計が可能になる。
    • 最適化された各部品は、抜き方向のアンダーカットがなく、完全に密閉された空洞を持たない形状となる。

4. 研究方法:

  • 研究デザイン:
    • 勾配ベースのマルチコンポーネントトポロジー最適化（MTO）フレームワークを拡張。
    • 新しい設計変数として、各コンポーネントのパーティングラインの位置と向きを導入。
    • パーティングラインを線形分類器として使用し、構造要素をコアとキャビティの半分にクラスタリング。
    • 数値的に近似された密度勾配を用いたベクトル法により、各金型半分のアンダーカットフィーチャと完全密閉された空洞の存在を評価。
  • データ収集方法:
    • 数値例による検証。コンプライアンス最小化問題を解き、提案手法の適用可能性を検証。
  • 分析方法:
    • 有限要素法を用いた構造解析。
    • 勾配ベースの最適化アルゴリズム。
    • ベクトル法とシグモイド関数を組み合わせた密度勾配法による抜き勾配と密閉空洞の評価。
  • 研究対象と範囲:
    • 2Dの構造アセンブリ。
    • ダイカストプロセスで製造される部品。
    • コンプライアンス最小化を目的関数とするトポロジー最適化。

5. 主な研究成果:

  • 主要な研究成果:
    • 提案されたMTO-D法は、ダイカストプロセスにおける製造制約を考慮したマルチコンポーネント構造のトポロジー最適化に有効であることを数値例で示した。
    • 最適化された結果は、各部品が抜き方向にアンダーカットがなく、完全に密閉された空洞を持たない、ダイカスト成形可能な形状であることを示した。
    • MTO-D法は、MTO-S法と比較して、ダイカスト部品の成形性を大幅に改善した。
    • 最大許容MABB面積 A* と最大許容コンポーネント数 K の設定が、最適化構造の性能に大きな影響を与えることを示した。
  • 統計的/定量的分析結果:
    • 図11, 12, 13, 15, 16, 17 に数値例の結果が示されている。
    • 図16 に示すように、A* の増加に伴い、最適化構造の体積率が増加し、構造コンプライアンスが減少するトレードオフ関係が示された。
    • 図17 に示すように、K の増加に伴い、最適化構造の体積率が増加し、構造コンプライアンスが減少するトレードオフ関係が示された。
  • データ解釈:
    • 提案手法は、ダイカスト部品の設計において、構造性能と製造コストのバランスを考慮した最適設計を支援する。
    • MTO-D法は、従来のモノリシックトポロジー最適化では達成できなかった、穴を持つアセンブリ構造を生成できることを示した（図11a, 11b）。
  • 図の名前リスト:
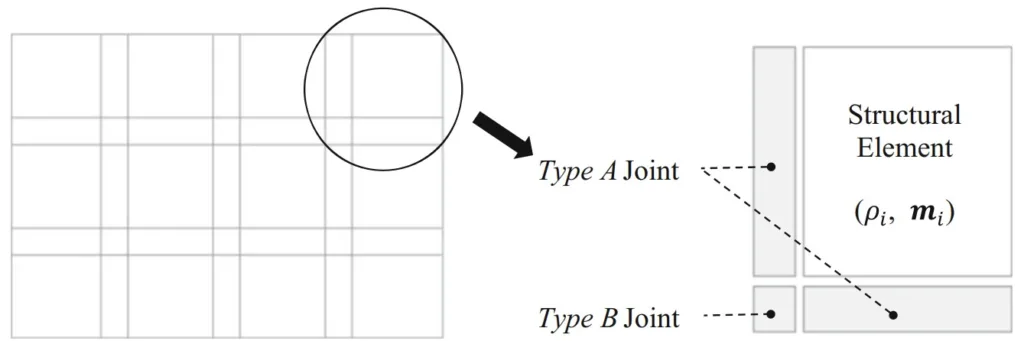
    • Fig. 1 Domain discretization and two different joint elements
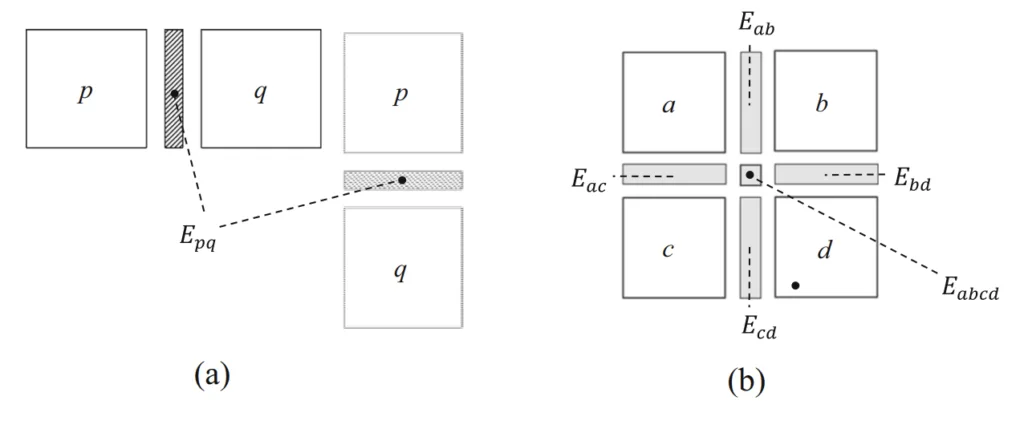
    • Fig. 2 Stiffness models of joint elements. a Type A joint element and b Type B joint element
    • Fig. 3 Geometry requirements for cast components: a internal cavity, b undercut, c modified parting line without undercut
    • Fig. 4 Cartesian representation of orientation in 2D
    • Fig. 5 Representations of parting line and the drawing direction
    • Fig. 6 Sigmoid function SL(x) for parting line
    • Fig. 7 detection of undercuts and internal cavities
    • Fig. 8 Sigmoid function Su(x) for undercut features
    • Fig. 9 Approximation of density gradient: a eight finite elements surrounding element i, and b four unit vectors for gradient approximation
    • Fig. 10 Design domain and boundary condition for three test problem. a Cantilever (2-by-1); b Bridge (4-by-1); c MBB (4-by-1)
    • Fig. 11 Optimized results for different boundary conditions. For each condition, the overall structure (first row), density for each component ρ (second row), and undercut features detection Undercut S(d(k) • ∇(k)ρi) • d(k) • ∇(k)ρi (third row) are plotted. The red and blue lines are plotted as drawing direction, the green line are parting line
    • Fig. 12 Comparison between the results (post-processed) with different grid sizes (left: 20×10, right: 40×20) in cantilever beam loading case: (a) Lower case; (b) Upper case
    • Fig. 13 Comparison between the results (post-processed) by MTO-D (left) and MTO-S (right): a bridge and b cantilever beam (upper loading)
    • Fig. 14 Iteration history curve for MBB beam example: a objective function and MABB area constraint and b moldability constraint
    • Fig. 15 Comparison between the results (post-processed) with different initial parting line direction for MBB beam example. For each direction (45/-45/30/60), the assembly and structure for each component are plotted. The red and blue lines are plotted as drawing direction, the green line are parting line
    • Fig. 16 Topology optimization results with different MABB limit value (red and blue lines: drawing direction, green line: parting line)
    • Fig. 17 Topology optimization results with different number of components (red and blue lines: drawing direction, green line: parting line): a cantilever beam (upper loading) and b MBB beam
Fig. 1 Domain discretization and two different joint elements
Fig. 1 Domain discretization and two different joint elements
Fig. 2 Stiffness models of joint elements. a Type A joint element and b Type B joint element
Fig. 2 Stiffness models of joint elements. a Type A joint element and b Type B joint element
Fig. 17 Topology optimization results with different number of components (red and blue lines: drawing direction, green line: parting line): a cantilever beam (upper loading) and b MBB beam
Fig. 17 Topology optimization results with different number of components (red and blue lines: drawing direction, green line: parting line): a cantilever beam (upper loading) and b MBB beam

6. 結論と考察:

  • 主な結果の要約:
    • ダイカストプロセス向けマルチコンポーネントトポロジー最適化手法（MTO-D）を提案し、その有効性を数値例で検証した。
    • MTO-D法は、各部品がダイカスト成形可能であり、アンダーカットや密閉空洞がない構造を設計できることを示した。
    • MTO-D法は、MTO-S法と比較して成形性を向上させた。
    • 最大許容MABB面積と最大許容コンポーネント数の設定が設計性能に影響を与えることを示した。
  • 研究の学術的意義:
    • ダイカストプロセスにおける製造制約を考慮したマルチコンポーネントトポロジー最適化の新しいフレームワークを提供した。
    • 密度勾配法とベクトル法を組み合わせた新しい抜き勾配・密閉空洞制約モデルを開発した。
    • パーティングラインの位置と向きを設計変数として導入し、最適化プロセスに組み込む新しい手法を提案した。
  • 実用的な意義:
    • ダイカスト部品の設計において、設計初期段階から製造可能性を考慮した最適設計を支援するツールを提供した。
    • 自動車部品などの構造アセンブリの軽量化、高性能化、製造コスト削減に貢献する可能性を示唆した。
  • 研究の限界:
    • 2D問題に限定した検証であり、3D問題への拡張が必要である。
    • アンダーカットフィーチャの検出において、要素の重心で代表されるため、わずかなアンダーカットが残る場合がある。
    • 製造コスト制約は、MABB面積のみを考慮した簡略化モデルであり、より詳細なコストモデルの導入が望ましい。

7. 今後のフォローアップ研究:

  • 今後の研究の方向性:
    • 3D実装の開発（最小体積境界ボックスモデリングと3Dジョイント剛性モデルに焦点を当てる）。
    • ジョイントの最大応力に関する追加制約の導入。
    • 異なるコンポーネント間の界面強度の影響の考慮。
    • 鋳造部品の溶接コストモデルの導入。
    • 非直線的なパーティングラインを許容するための緩和。
    • サイドピンやコアリフターなどの追加の金型機構のコストモデルに基づくアンダーカット制約。
    • より一般的な密度勾配計算の定式化。

8. 参考文献:

  • Altair Engineering, Inc (2017) Altair HyperWorks 2017.1 user's manual, www.altairhyperworks.com/product/OptiStruct
  • Bendsøe MP, Kikuchi N (1988) Generating optimal topologies in structural design using a homogenization method. Comput Methods Appl Mech Eng 71(2):197-224
  • Boothroyd G, Dewhurst P, Knight WA (2010) Product design for manufacture and assembly. CRC Press, Boca Raton
  • Bruyneel M, Fleury C (2002) Composite structures optimization using sequential convex programming. Adv Eng Softw 33(7-10):697-711
  • Chen J, Shapiro V, Suresh K, Tsukanov I (2007) Shape optimization with topological changes and parametric control. Int J Numer Methods Eng 71(3):313-346
  • Chickermane H, Gea HC (1997) Design of multi-component structural systems for optimal layout topology and joint locations. Eng Comput 13(4):235-243
  • Fu MW, Nee AY, Fuh JY (2002) The application of surface visibility and moldability to parting line generation. Comput Aided Des 34(6): 469-480
  • Gaynor AT, Guest JK (2016) Topology optimization considering overhang constraints: eliminating sacrificial support material in additive manufacturing through design. Struct Multidiscip Optim 54(5): 1157-1172
  • Gersborg AR, Andreasen CS (2011) An explicit parameterization for casting constraints in gradient driven topology optimization. Struct Multidiscip Optim 44(6):875-881
  • Guest JK, Asadpoure A, Ha SH (2011) Eliminating beta-continuation from Heaviside projection and density filter algorithms. Struct Multidiscip Optim 44(4):443-453
  • Guirguis D, Hamza K, Aly M, Hegazi H, Saitou K (2015) Multi-objective topology optimization of multi-component continuum structures via a Kriging-interpolated level set approach. Struct Multidiscip Optim 51(3):733-748
  • Guo X, Zhou J, Zhang W, Du Z, Liu C, Liu Y (2017) Self-supporting structure design in additive manufacturing through explicit topology optimization. Comput Methods Appl Mech Eng 323:27-63
  • Harzheim L, Graf G (2006) A review of optimization of cast parts using topology optimization. Struct Multidiscip Optim 31(5):388-399
  • Hicks J (1999) Welded joint design, 3rd edn. Industrial Press, New York
  • Hughes TJ (2000) The finite element method: linear static and dynamic finite element analysis. Dover Publications, MI
  • Jiang T, Chirehdast M (1997) A systems approach to structural topology optimization: designing optimal connections. J Mech Des 119(1): 40-47
  • Johanson R, Kikuchi N, Papalambros P (1994) Simultaneous topology and material microstructure design. Adv Struct Optim:143-149
  • Kang Z, Wang Y, Wang Y (2016) Structural topology optimization with minimum distance control of multiphase embedded components by level set method. Comput Methods Appl Mech Eng 306:299-318
  • Langelaar M (2017) An additive manufacturing filter for topology optimization of print-ready designs. Struct Multidiscip Optim 55(3): 871-883
  • Li Q, Chen W, Liu S, Fan H (2018) Topology optimization design of cast parts based on virtual temperature method. Comput Aided Des 94: 28-40
  • Li Q, Steven GP, Xie YM (2001a) Evolutionary structural optimization for connection topology design of multi-component systems. Eng Comput 18(3/4):460-479
  • Li Y, Xin X, Kikuchi N, Saitou K (2001b) Optimal shape and location of piezoelectric materials for topology optimization of flextensional actuators. In Proceedings of the 3rd annual conference on genetic and evolutionary computation (pp. 1085-1090). Morgan Kaufmann Publishers Inc.
  • Lim JY, Yoon MJ, Kim SY, Shin HS, Kim TG (2015) Mechanical properties of CO2/MIG welded structural rolled steel and stainless steel. J Mech Sci Technol 29(1):103-108
  • Liu J, Gaynor AT, Chen S, Kang Z, Suresh K, Takezawa A, Cheng L. (2018) Current and future trends in topology optimization for additive manufacturing. Struct Multidiscip Optim 57(6):2457-2483.
  • Liu P, Kang Z (2018) Integrated topology optimization of multi-component structures considering connecting interface behavior. Comput Methods Appl Mech Eng 341:851-887
  • Liu S, Li Q, Chen W, Tong L, Cheng G (2015) An identification method for enclosed voids restriction in manufacturability design for additive manufacturing structures. Front Mech Eng 10(2):126-137
  • Lyu N, Saitou K (2005) Topology optimization of multicomponent beam structure via decomposition-based assembly synthesis. J Mech Des 127(2):170-183
  • MathWorks, Inc (2016) MATLAB Primer, R2016a edition. www. mathworks.com
  • Mirzendehdel AM, Suresh K (2016) Support structure constrained topology optimization for additive manufacturing. Comput Aided Des 81:1-13
  • Nomura T, Dede EM, Lee J, Yamasaki S, Matsumori T, Kawamoto A, Kikuchi N (2015) General topology optimization method with continuous and discrete orientation design using isoparametric projection. Int J Numer Methods Eng 101(8):571-605
  • Qian X (2017) Undercut and overhang angle control in topology optimization: a density gradient based integral approach. Int J Numer Methods Eng 111(3):247-272
  • Qian Z, Ananthasuresh GK (2004) Optimal embedding of rigid objects in the topology design of structures. Mech Based Des Struct Mach 32(2):165-193
  • Ravi B, Srinivasan MN (1990) Decision criteria for computer-aided parting surface design. Comput Aided Des 22(1):11-18
  • Rozvany GI, Zhou M, Birker T (1992) Generalized shape optimization without homogenization. Struct Optim 4(3–4):250-252
  • Sato Y, Yamada T, Izui K, Nishiwaki S (2017) Manufacturability evaluation for molded components using fictitious physical models, and its application in topology optimization. Int J Adv Manuf Technol 92(1-4):1391-1409
  • Sigmund O (2001) A 99 line topology optimization code written in Matlab. Struct Multidiscip Optim 21(2):120-127
  • Stegmann J, Lund E (2005) Discrete material optimization of general composite shell structures. Int J Numer Methods Eng 62(14): 2009-2027
  • Vanderplaats Research and Development, Inc (2017) GENESIS 16.0 User's Manual, www.vrand.com/products/genesis/
  • Vatanabe SL, Lippi TN, de Lima CR, Paulino GH, Silva EC (2016) Topology optimization with manufacturing constraints: a unified projection-based approach. Adv Eng Softw 100:97-112
  • Wang Y, Gao J, Kang Z (2018) Level set-based topology optimization with overhang constraint: towards support-free additive manufacturing. Comput Methods Appl Mech Eng 339:591-614
  • Wang Y, Kang Z (2017) Structural shape and topology optimization of cast parts using level set method. Int J Numer Methods Eng 111(13): 1252-1273
  • Wang X, Kang Z, Wang Y (2011) Topology design of slender piezoelectric actuators with repetitive component patterns. J Intell Mater Syst Struct 22(18):2161-2172
  • Wang MY, Wang X, Guo D (2003) A level set method for structural topology optimization. Comput Methods Appl Mech Eng 192(1- 2):227-246
  • Weinstein M, Manoochehri S (1997) Optimum parting line design of molded and cast parts for manufacturability. J Manuf Syst 16(1):1
  • Xia Q, Shi T, Wang MY, Liu S (2010) A level set based method for the optimization of cast part. Struct Multidiscip Optim 41(5):735–747
  • Yildiz AR, Saitou K (2011) Topology synthesis of multicomponent structural assemblies in continuum domains. J Mech Des 133(1):011008
  • Zhang W, Zhou L (2018) Topology optimization of self-supporting structures with polygon features for additive manufacturing. Comput Methods Appl Mech Eng 334:56-78
  • Zhou M, Fleury R, Shyy YK, Thomas H, and Brennan J (2002) Progress in topology optimization with manufacturing constraints. In 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization (p. 5614)
  • Zhou Y, Saitou K (2017) Topology optimization of composite structures with data-driven resin filling time manufacturing constraint. Struct Multidiscip Optim 55(6):2073-2086
  • Zhou Y, Saitou K (2018) Gradient-based multi-component topology optimization for stamped sheet metal assemblies (MTO-S). Struct Multidiscip Optim 58(1):83-94
  • Zhou Y, Nomura T, Saitou K (2018) Multi-component topology and material orientation design of composite structures (MTO-C). Comput Methods Appl Mech Eng 342:438-457
  • Zhou Y, Nomura T, Saitou K (2019) Multicomponent topology optimization for additive manufacturing with build volume and cavity free constraints. J Comput Inf Sci Eng 19(2):021011
  • Zhu JH, Gu XJ, Zhang WH, Beckers P (2013) Structural design of aircraft skin stretch-forming die using topology optimization. J Comput Appl Math 246:278-288
  • Zhu J, Zhang W, Beckers P, Chen Y, Guo Z (2008) Simultaneous design of components layout and supporting structures using coupled shape and topology optimization technique. Struct Multidiscip Optim 36(1):29-41
  • Zhu JH, Zhang WH, Xia L (2016) Topology optimization in aircraft and aerospace structures design. Archiv Comput Methods Eng 23(4): 595-622

9. 著作権:

この資料は上記論文に基づいて要約したものであり、商業目的での無断利用は禁止されています。
Copyright © 2025 CASTMAN. All rights reserved.

PDF View

Tags: Applications; ,CAD; ,Die casting; ,Efficiency; ,Microstructure; ,Review; ,金型; ,금형; ,자동차; ,해석