AlSiCu合金の凝固解析を革新する：動的ベースラインアプローチによる鋳造シミュレーションの精度向上

Fraction solid evolution characteristics of AlSiCu alloys - dynamic baseline approach

この技術概要は、P. Marchwica, J.H. Sokolowski, W.T. Kierkusによる学術論文「Fraction solid evolution characteristics of AlSiCu alloys - dynamic baseline approach」に基づいています。この論文は、Journal of Achievements in Materials and Manufacturing Engineering (2011)に掲載されました。

キーワード

• 主要キーワード: AlSiCu合金 凝固解析
• 副次キーワード: 動的ベースライン, 固体率, 鋳造シミュレーション, 熱分析, 欠陥予測

エグゼクティブサマリー

• 課題: 鋳造シミュレーションの精度は、合金の凝固挙動（固体率の推移）を正確に把握することに依存しており、不正確なデータはコストのかかる試作や欠陥の原因となります。
• 手法: 改良された熱分析手法「動的ベースラインアプローチ」を用い、冷却曲線から合金固有の凝固特性を物理的に意味のある形で定量化しました。
• 重要なブレークスルー: AlSiCu合金の化学成分（Si、Cu濃度）と、凝固過程における重要な温度・固体率との間の強力な相関関係を特定し、凝固挙動の予測モデルを構築しました。
• 結論: この研究は、鋳造シミュレーションの精度を飛躍的に向上させ、合金設計やプロセス最適化を加速させるための、信頼性の高いデータと手法を提供します。

課題：なぜこの研究がHPDC専門家にとって重要なのか

高圧ダイカスト（HPDC）の現場では、湯流れや凝固のシミュレーションが不可欠です。しかし、そのシミュレーション結果が現実と乖離することは珍しくありません。特に、アルミニウム合金が液体から固体へと変化する「凝固過程」の挙動、すなわちどの温度でどれくらいの割合が固まっているか（固体率）を正確にモデル化することは、極めて困難でした。

従来のモデルは多くの仮定に基づいていたため、特定の合金や鋳造条件での正確性に欠けていました。この不確実性が、ひけ巣や凝固割れといった鋳造欠陥の予測を難しくし、結果として開発リードタイムの長期化や、コストのかかる金型修正、試作の繰り返しにつながっていました。全てのエンジニアが直面するこの「シミュレーションと現実のギャップ」を埋める、より信頼性の高い凝固解析手法が求められていたのです。

アプローチ：その方法論を解き明かす

本研究では、この課題を解決するために「動的ベースライン（Dynamic Baseline, DBL）アプローチ」という先進的な熱分析手法を適用しました。これは、従来の単純化されたモデルとは一線を画すものです。

• 手法1：改良型冷却曲線解析（CA-CCA） 研究チームは、合金サンプルが冷却される際の温度変化を精密に測定しました。この冷却曲線データから、もし相変態（凝固）が起こらなかった場合にたどるであろう理論的な冷却曲線、すなわち「動的ベースライン」を数学的に導出します。このベースラインと実際の冷却曲線との差分が、凝固によって放出される潜熱に相当します。この差分を積分することで、任意の温度における固体率（fs）を極めて高い精度で算出できるのです。この解析には、UMSA（Universal Metallurgical Simulator and Analyzer）やAlTAP（Aluminum Thermal Analysis Platform）といった専用の解析プラットフォームが使用されました。
• 手法2：厳密な実験条件 データの信頼性を確保するため、実験は厳密に管理されました。例えば、サンプルの熱容量に対して無視できるほど軽量なステンレス箔製のるつぼや、応答性の高い熱電対を使用することで、測定機器が冷却挙動に与える影響を最小限に抑えました。これにより、合金そのものの純粋な凝固特性を捉えることが可能になりました。

ブレークスルー：主要な研究結果とデータ

このアプローチにより、AlSiCu合金の凝固に関する非常に価値のある知見が得られました。

発見1：化学成分が凝固挙動に与える影響の定量化

本研究では、合金の主要な添加元素であるシリコン（Si）と銅（Cu）の濃度が、凝固開始温度（液相線温度）や凝固完了までの温度範囲にどのような影響を与えるかを明確にしました。

論文のFigure 24に示されているように、SiとCuの濃度が増加するにつれて、凝固開始温度は620℃以上から580℃以下まで顕著に低下する傾向が確認されました。これにより、化学成分から凝固プロセスの主要パラメータを予測することが可能になります。

発見2：信頼性の高い予測モデルの構築

本研究の最も重要な成果は、合金の化学成分と凝固過程の各イベント（α-Alデンドライト晶出、Al-Si共晶反応など）の発生温度・固体率との間に、非常に強い相関関係があることを見出した点です。

論文のTable 4が示すように、ほとんどのパラメータにおいて、化学成分から凝固特性を予測する多項式モデルの決定係数（R²）が0.80を超える高い値を示しました。これは、開発されたモデルが非常に信頼性が高く、実用的な予測ツールとして機能することを意味します。エンジニアは、合金の化学成分さえわかれば、その凝固挙動を高精度で予測できるのです。

研究開発および製造現場への実用的な示唆

• プロセスエンジニア向け： この研究データは、特定の合金に対して最適な冷却速度や金型温度を設定するための強力な指針となります。凝固挙動を正確に予測することで、微細組織を制御し、ひけ巣などの欠陥を低減させることが期待できます。
• 品質管理チーム向け： 論文のFigure 24からFigure 41に示されるデータは、化学成分のわずかなばらつきが凝固特性にどのように影響するかを示しています。これは、製品の機械的特性のばらつき原因を特定し、新たな品質検査基準を設ける上で役立ちます。
• 設計エンジニア向け： 開発された予測モデルを活用することで、設計の初期段階で、求められる特性を持つ最適な合金組成を選定することが可能になります。これにより、手戻りを減らし、開発サイクルを大幅に短縮できます。

論文詳細

Fraction solid evolution characteristics of AlSiCu alloys - dynamic baseline approach

1. 概要:

• Title: Fraction solid evolution characteristics of AlSiCu alloys - dynamic baseline approach
• Author: P. Marchwica, J.H. Sokolowski, W.T. Kierkus
• Year of publication: 2011
• Journal/academic society of publication: Journal of Achievements in Materials and Manufacturing Engineering (VOLUME 47, ISSUE 2, August 2011)
• Keywords: Aluminum alloys; Baseline; Fraction solid; Thermal analysis

2. Abstract:

Purpose: The goal of the research presented in this paper is to gain a deeper understanding of dynamic solidification processes of metals and alloys through application of improved baseline and fraction solid methodologies to hypoeutectic aluminum-silicon alloys with varying concentrations of silicon and copper. Design/methodology/approach: The paper makes use of numerical models developed at the University of Windsor, including Newtonian Computer-Aided Cooling Curve Analysis and the Silicon Equivalency algorithm. Co-developed thermal analysis platforms are also used, including the Universal Metallurgical Simulator and Analyzer (UMSA) and the Aluminum Thermal Analysis Platform (AlTAP). Findings: This paper identifies key temperature and fraction solid values for hypoeutectic AlSiCu alloys across a wide range of chemistries. The paper also provides correlations whereby temperature/fraction solid values for metallurgical reactions can be predicted on the basis of chemistry. Research limitations/implications: Future work for the project will expand upon the relationships between important metallurgical events and alloy chemistries and derive general trends to enhance predictive capabilities. Practical implications: The data and techniques used in this paper may be used in order to improve simulations of casting processes. The relationships between solidification events and alloy chemistries will aid in the design and optimization of casting alloys and components. Originality/value: This paper would be of value to members of the engineering community who need precise information about fraction solid for use in designing alloys or optimizing technology and simulations of casting processes.

3. Introduction:

本稿は、先進的熱分析（Advanced Thermal Analysis）が金属および合金の凝固に関する定量的な冶金学的情報を提供できる点に着目している。特に、凝固潜熱、固体率（fs）の推移、デンドライトコヒーレンシーポイントなどの特性評価の重要性を述べている。これらのデータを正確に抽出するためには、動的ベースライン曲線（Dynamic Baseline curve, DBL）の算出が不可欠である。DBLは、相変態が起こらなかった場合の仮説的な冷却曲線（の一次導関数）を表し、材料とプロセスの特性を反映する。本稿の目的は、この改良されたベースラインおよび固体率の解析手法を、シリコンと銅の濃度が異なる亜共晶アルミニウム-シリコン合金に適用し、その動的な凝固プロセスへの理解を深めることにある。

4. 研究の概要:

研究トピックの背景:

鋳造合金の設計、鋳造方案の最適化、およびオンラインでのプロセス制御を成功させるためには、固体率（fs）の推移など、凝固現象に関する定量的な知識が不可欠である。凝固速度は鋳造品の断面厚や形状によって異なり、それが最終的な鋳造組織（相の種類、形態、健全性など）に直接影響を与える。

先行研究の状況:

過去35年間にわたり、凝固プロセスのDBL方程式を実験的に決定するための様々な手法が提案されてきた。これらは主に、ニュートン解析、フーリエ解析、経験的解析の3つに分類される。また、固体率を決定する手法も、DSC/DTAのような熱分析、計算熱力学ソフトウェア、焼入れ組織の定量的金属組織解析など多岐にわたるが、それぞれにサンプルサイズの制約や単純化された仮定といった限界があった。特に、工業的に複雑な合金やプロセスに適用するには、より実現象に即した解析手法が求められていた。

研究の目的:

本研究の目的は、改良されたベースラインおよび固体率の解析手法を、SiとCuの濃度を様々に変化させた亜共晶AlSiCu合金に適用することである。これにより、これらの合金の動的な凝固プロセスに関するより深い理解を得ることを目指す。具体的には、広範な化学組成にわたって主要な凝固イベント（反応）に対応する温度と固体率の値を特定し、化学組成に基づいてこれらの値を予測するための相関関係を構築する。

中核研究:

本研究の中核は、ウィンザー大学で開発されたニュートンモデルに基づく冷却曲線解析（CA-CCA）手法を用いて、AlSiCu合金の凝固挙動を詳細に分析することにある。Si濃度を5, 7, 9, 11 wt%、Cu濃度を1, 2, 4 wt%の範囲で変化させた12種類の実験合金を作製した。各合金の冷却曲線を精密に測定し、動的ベースライン（DBL）を算出。DBLと実測の冷却曲線（の一次導関数）との差分から、凝固過程における固体率（fs）の温度に対する推移を算出した。最終的に、得られた凝固特性（液相線温度、固相線温度、共晶反応温度、各イベントでの固体率など）と、化学組成（シリコン当量SiEQおよびCu濃度）との間の関係性を3次元グラフと相関分析によってモデル化した。

5. 研究方法論

研究デザイン:

本研究は、実験的アプローチを採用しており、制御された条件下での熱分析を通じてAlSiCu合金の凝固特性を定量化する。

データ収集・分析方法:

12種類の異なる化学組成を持つ3XX系アルミニウム合金を、高純度アルミニウムとマスターアロイを用いて製造した。サンプルは、不活性ガス雰囲気下で再溶解され、鋳造された。温度測定には、ニュートン冷却モデルの要件を満たすよう特別に設計された超軽量のステンレス鋼箔製カップと、高感度のK型熱電対が使用された。高速データ収集システムを用いて冷却曲線データを記録した。 分析は、以下の手順で行われた。 1. 冷却曲線（温度 vs. 時間）とその一次導関数（dT/dt）を算出する。 2. 完全に液体および固体である領域のdT/dtデータを用いて、3次の多項式をフィッティングし、動的ベースライン（DBL）方程式を決定する。 3. DBLと実測のdT/dt曲線との間の面積を積分することにより、各温度における固体率（fs）を算出する。 4. 得られた凝固特性値（温度、固体率）を、化学組成（SiEQ、Cu濃度）に対してプロットし、相関関係を評価した。

研究対象と範囲:

研究対象は、Si濃度が約5 wt%から11 wt%、Cu濃度が約1 wt%から4 wt%の範囲にある亜共晶AlSiCu合金である。本研究は、これらの合金の凝固過程における固体率の推移特性に焦点を当てている。

6. 主要な結果:

主要な結果:

• 本稿で採用された動的ベースライン（DBL）法は、純金属（スズ、アルミニウム）および356合金において高い相関係数（R² > 0.99）を示し、物理的に意味のある熱損失関数を単一の連続関数で表現できることを実証した。
• AlSiCu合金の液相線温度は、SiEQおよびCu濃度の上昇に伴い大幅に低下（64.9℃の範囲で変化）する一方、固相線温度はほぼ一定（477.1-484.8℃）であった。これにより、合金元素濃度が高いほど凝固温度範囲は狭くなる傾向が見られた。
• α-Alデンドライト核生成、Al-Si共晶反応など、主要な冶金学的反応における温度および固体率の値が、調査した12種類の合金すべてについて特定・定量化された。
• 合金の化学組成（SiEQ、Cu）と、凝固特性（温度、固体率）との間に強力な相関関係が確認された。特に2次の多項式平面でフィッティングした場合、18のパラメータのうち15で決定係数（R²）が0.80を超え、化学組成に基づく凝固挙動の予測モデルの妥当性が示された（Table 4）。

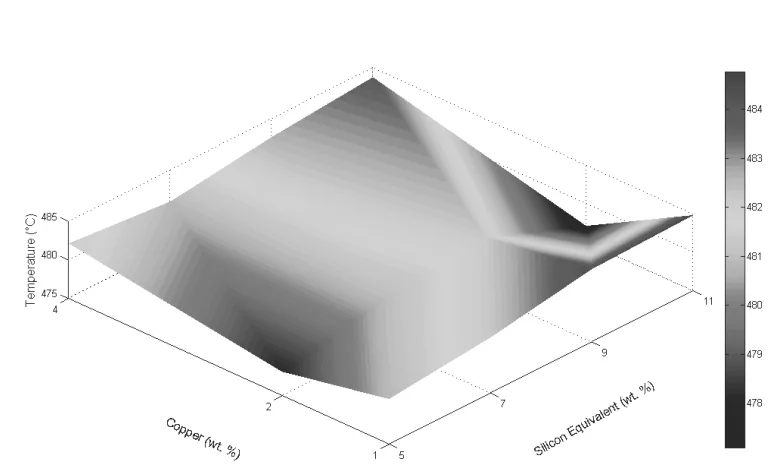
Figure Name List:

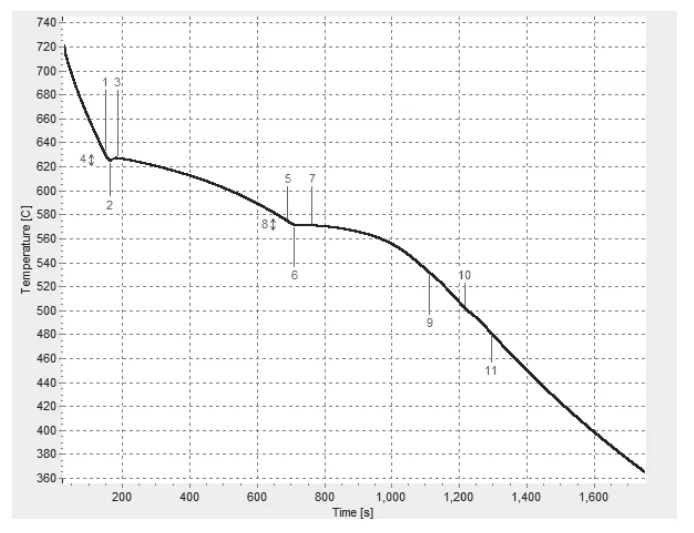
• Fig. 1. Temperature vs. Time Cooling Curve of a Nominal 5 wt.% Si and 1 wt.% Cu Aluminum Alloy
• Fig. 2. First Derivative vs. Temperature Cooling Curve of a Nominal 5 wt.% Si and 1 wt.% Cu Aluminum Alloy with Overlaid Dynamic Baseline
• Fig. 3. Fraction Solid Curve of a Nominal 5 wt.% Si and 1 wt.% Cu Aluminum Alloy with Metallurgical Events Indicated
• Fig. 4. Aluminum Silicon Binary Phase Diagram [48]
• Fig. 5. Cooling Curve for the 319.2 Aluminum Alloy
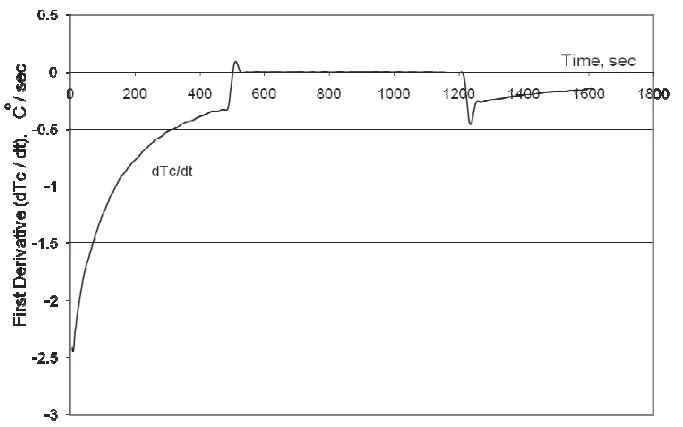
• Fig. 6. First Derivative of the Cooling Curve for the 319.2 Aluminum Alloy
• Fig. 7. Regression Equation of the Dynamic Baseline (DBL) for the 319.2 Aluminum Alloy
• Fig. 8. First Derivative of the Cooling Curve and the Dynamic Baseline (DBL) for the 319.2 Aluminum Alloy
• Fig. 9. Cooling Curve for Tin with a Purity of 99.95%
• Fig. 10. First derivative of the Cooling Curve for tin with a purity of 99.95%
• Fig. 11. Regression equation of the Dynamic Baseline (DBL) for tin with a purity of 99.95%
• Fig. 12. First derivative of the Cooling Curve and the dynamic Baseline (DBL) for pure tin
• Fig. 13. UMSA first derivatives of the heating and cooling curves for the 319.2 alloy test sample
• Fig. 14. Solidification of Near Pure Aluminum at Moderate Cooling Rates
• Fig. 15. Fraction Solid Curve for Industrially Pure Tin
• Fig. 16. Solidification of A356 Alloy at Medium Cooling Rates
• Fig. 17. Solidification of A356 Alloy at Moderate Cooling Rates
• Fig. 18. Solidification of A356 Alloy at Medium Cooling Rates
• Fig. 19. Solidification of A356 Alloy at Medium Cooling Rates
• Fig. 20. Matrix of Si and Cu Nominal Compositions (wt.%) used in experiments with overlaid compositions of selected 3XX alloys
• Fig. 21 - Fraction Solid Temperature Dependence for Nominal 1wt.% Cu and Nominal 5, 7, 9 and 11 wt.% Si
• Fig. 22. Fraction Solid Temperature Dependence for Nominal 2wt.% Cu and Nominal Si 5, 7, 9 and 11 wt.% Si
• Fig. 23. Fraction Solid Temperature Dependence for Nominal 4.wt.% Cu and Nominal 5, 7, 9 and 11 wt.% Si
• Fig. 24. Tα,DEN NUC - Nucleation Temperature of αAl Dendrite Network (°C) vs. Cu (wt.%) and SiEQ (wt.%)
• Fig. 25. Tα,DEN MIN - Temperature of αAl Dendrite Network Minimum (°C) vs. Cu (wt.%) and SiEQ (wt.%)
• Fig. 26. fsα,DEN MIN - Fraction Solid at αAl Dendrite Network Minimum Temperature (%) vs. Cu (wt.%) and SiEQ (wt.%)
• Fig. 27. Tα,DEN G - Temperature of αAl Dendrite Network Growth (°C) vs. Cu (wt.%) and SiEQ (wt.%)
• Fig. 28. fsα,DEN G - Fraction Solid at αAl Dendrite Network Growth Temperature (%) vs. Cu (wt.%) and SiEQ (wt.%)
• Fig. 29. Tα,DEN UNDER - αAl Dendrite Network Undercooling (°C) vs. Cu (wt.%) and SiEQ (wt.%)
• Fig. 30. fsα,DEN UNDER - Fraction Solid Difference of αAl Dendrite Network Undercooling (%) vs. Cu (wt.%) and SiEQ (wt.%)
• Fig. 31. TAlSi E NUC - Temperature of AlSi Eutectic Nucleation (°C) vs. Cu (wt.%) and SiEQ (wt.%)
• Fig. 32. fsAlSi E NUC - Fraction Solid at AlSi Eutectic Nucleation Temperature (%) vs. Cu (wt.%) and SiEQ (wt.%)
• Fig. 33. TAlSi E MIN - Temperature of AlSi Eutectic Minimum (°C) vs. Cu (wt.%) and SiEQ (wt.%)
• Fig. 34. fsAlSi E MIN - Fraction Solid at AlSi Eutectic Minimum Temperature (%) vs. Cu (wt.%) and SiEQ (wt.%)
• Fig. 35. TAlSi E G - Temperature of AlSi Eutectic Growth (°C) vs. Cu (wt.%) and SiEQ (wt.%)
• Fig. 36. fsAlSi E G - Fraction Solid at AlSi Eutectic Growth Temperature (%) vs. Cu (wt.%) and SiEQ (wt.%)
• Fig. 37. TAlSi UNDER - AlSi Eutectic Undercooling (°C) vs. Cu (wt. %) and SiEQ (wt.%)
• Fig. 38. fsAlSi UNDER - Fraction Solid Difference of AlSi Eutectic Undercooling (%) vs. Cu (wt.%) and SiEQ (wt.%)
• Fig. 39. TAlSiCuMg - Temperature of AlSiCuMg Eutectic (°C) vs. Cu (wt.%) and SiEQ (wt.%)
• Fig. 40. fsAlSiCuMg - Fraction Solid at AlSiCuMg Eutectic Temperature (%) vs. Cu (wt.%) and SiEQ (wt.%)
• Fig. 41. Tsol - Solidus Temperature (°C) vs. Cu (wt.%) and SiEQ (wt.%)

7. Conclusion:

本研究は、凝固する試験サンプルからの熱損失を記述するために、単一かつ固有の「全体熱伝達係数」U(Tc)関数を使用することが可能であり、正当であることを実証した。このアプローチによって導出された動的ベースライン（DBL）は、実際の測定値から得られる滑らかで不連続性のない関数であり、試験された材料およびプロセスのパラメータを正確に反映する。このDBL関数を用いることで、記録された凝固温度のみに基づいて固体率を算出する手法を開発した。Si/Cu含有量を変化させた実験から得られた結果は、固体率の推移に定量化可能な傾向が存在し、多くの場合で高い相関性を持つことを示した。この固体率に関する情報は、現行の商用合金に適用できるだけでなく、調査範囲外の化学組成を持つAlSi合金の固体率推移を予測するための合理的なモデルとしても機能しうる。

8. References:

• [1] M.B. Djurdjevic, W. Kasprzak, C.A. Kierkus, J.H. Sokolowski, Quantification of Cu enriched phases in synthetic 3XX aluminum alloys using the thermal analysis technique, AFS Transactions, 2001.
• [2] M. Djurdjevic, P. Gallo, H. Jiang, J.H. Sokolowski, Evaluation of strontium fading in the 319 aluminum alloy using thermal analysis, AFS Transactions 20 (2000) 485-486.
• [3] M. Djurdjevic, T. Stockwell and J. H. Sokolowski, The effect of strontium on the microstructure of aluminum-silicon and aluminum-copper eutectics in the 319 Alloy, International Journal of Cast Metals Research 12 (1999) 67-73.
• [4] M. Djurdjevic, W.T. Kierkus, R. Liliak, J.H. Sokolowski, Extended analysis of cooling curves, Proceedings of the 41st Conference of Metallurgists COM’2002, Montreal, 2002.
• [5] H. Jiang, W. Kierkus and J. H. Sokolowski, Dendrite coherency point determination using thermal analysis and rheological measurements, Proceedings of the International Conference on Thermophysical Properties of Materials TPPM’99, Singapore, 1999.
• [6] R. MacKay, M. Djurdjevic, J.H. Sokolowski, W. Evans, Using the method of a in-situ thermal analysis array in a cast section to assess riser feeding efficiency, Proceedings of the 131st TMS Annual Meeting, Seattle, Washington, 2002, 17-21.
• [7] R. MacKay, M. Djurdjevic, et al., Effect of cooling rate on fraction solid of metallurgical reactions in 319 alloy, AFS Transactions 25 (2000) 521-529.
• [8] X. Chen, W. Kasprzak, J.H. Sokolowski, Reduction of the heat treatment process for the Al-based alloys by utilization of heat from solidification process, Journal of Materials Processing Technology 176 (2006) 24-31.
• [9] L. Bäckerud, G. Chai, J. Tamminen, Solidification characteristics of aluminum alloys, AFS-Skanaluminium, 1990.
• [10] R. Mackay, J. Sokolowski, Experimental observations of dendrite coarsening and Al-Si eutectic growth in progressively quenched structures of Al-Si-Cu casting alloys, International Journal of Metalcasting Spring (2008) 57-80.
• [11] J. Barlow, D.M. Stefanescu, Computer aided cooling curve analysis revisited, unpublished, 1996.
• [12] W.T. Kierkus, J.H. Sokolowski, Recent advances in cooling curve analysis: A new method of determining the ‘Base Line’ equation, AFS Transactions 66 (1999) 161-167.
• [13] E. Fras, W. Kapturkiewicz, A. Burbielko, H.F. Lopez, A New concept in thermal analysis of castings, AFS Transactions 101 (1993) 505-511.
• [14] D. Emadi, L. Whiting, M. Djurdjevic, W.T. Kierkus, J.H. Sokolowski, Comparison of newtonian and fourier thermal analysis techniques for calculation of latent heat and solid fraction of aluminum alloys, Metalurgija (2004) 91-106.
• [15] D.M. Stefanescu, G. Upadhya, D. Bandyopadhyay, Heat transfer-solidification kinetics modeling of solidifcation of castings, Metallurgical Transactions A 21 (1990) 997-1005.
• [16] D.M. Stefanescu, Solidification of flake, compacted, vernicular and spheroidal graphite cast irons as revealed by thermal analysis and directional solidification experiments, Material Research Society Symposium Proceedings, 34, 1985.
• [17] K.G. Upadhya, D.M. Stefanescu, K. Lieu, D.P. Yaeger, Computer-aided cooling curve analysis: principles and applications in metal casting, AFS Transactions 97 (1989) 61-66.
• [18] S.H. Jong, W.S. Hwang, Study of functional relationships of fraction solid with temperature in mushy range for the A356 Al alloy, AFS Transactions 92 (1992) 939-946.
• [19] J. Tamminen, Thermal analysis for investigation of solidification mechanisms in metals and alloys, Chemical Communications, University of Stockholm, 1988.
• [20] L. Arnberg, L. Bäckerud, Solidification characteristics of aluminum alloys, Vol. 3: Dendrite coherency, American Foundrymen’s Society, Inc, 1996.
• [21] H. Jiang, W.T. Kierkus, J.H. Sokolowski, Determining dendrite coherency point characteristics of Al alloys using single-thermocouple technique, AFS Transactions 68 (1999) 169-172.
• [22] R. Chavez-Zamarripa, J. Angelica Ramos-Salas, J. Talamentes-Silva, S. Valtierra, R. Colas, Determination of the dendrite coherency point during solidification by means of thermal diffusivity, Metallurgical and Materials Transactions A 38 (2007) 1875-1879
• [23] S. Gowri, Comparison of thermal analysis parameters of 356 and 359 alloys, AFS Transactions 94-29 (1994) 503-508.
• [24] H.G. Kang, H. Miyahara, K. Ogi, Influence of cooling rate and additions of Sr and Ti-B on solidification structures of AC4B type alloy, Proceedings of the 3rd Asian Foundry Congress, edited by Z.H. Lee, C.P. Hong, M.H. Kim, The Korean Foundrymen’s Society, Kyongju, Korea, 1995, 108-115.
• [25] Y.F. Chen, S.H. Jong, W.S. Hwang, The effect of cooling rate on the latent heat released mode for near pure aluminum and aluminum silicon alloy, Modelling of casting, welding and advanced solidification processes VII Edition by M. Cross, J. Campbell, The Minerals, Metals and Materials Society (1995) 483-490.
• [26] L. Ananthanarayanan, F.H. Samuel, J. Gruzleski, The thermal analysis studies on the effect of cooling rate on the microstructure of the 319 aluminum alloy, AFS Transactions 92-141, 383-391.
• [27] A.M. Figueredo, Y. Sumartha, M.C. Flemings, Measurement and calculation of solid fraction in quenched semi-solid melts of rheocast aluminum alloy A357, Light Metals edited by Barry Welch, The Minerals, Metals and Materials Society, 1998, 1103-1106.
• [28] G. Chai, Dendrite coherency during equiaxed solidification in aluminum alloys, Ph.D. Thesis, Department of Structural Chemistry, Arrhenius Laboratory, Stockholm University, 1994.
• [29] L. Arnberg, L. Bäckerud, G. Chai, Solidification characteristics of aluminum alloys, Vol. 3: Dendrite Coherency, American Foundrymen’s Society, Inc., Des Plaines, 1996.
• [30] E. Tzimas, A. Zavaliangos, Evaluation of volume fraction of solid in alloys formed by semisolid processing", Journal of Materials Science 35 (2000) 5319-5329.
• [31] J. Wannasin, R. Canyook, R. Burapa, L. Sikong, M.C. Flemings, Evaluation of solid fraction in a rheocast aluminum die casting alloy by a rapid quenching method, Scripta Materialia 59 (2008) 1091-1094.
• [32] M.C. Flemings, Solidification processing, McGraw-Hill, Inc., 1972.
• [33] S. Ohta, K. Asai, The behaviour of temperature decreasing and fraction solid increasing in solid-liquid coexisting zone in solidification process of aluminum alloy weld metal, Transactions of the Japan Welding Society 24/2 (1993) 131-139.
• [34] N. Saunders, Phase diagram calculations for commercial Al-alloys, Material Science Forum SF2M and INPG, Grenoble, 217-222/2 (1996) 667-672.
• [35] J.H. Chen, H.L. Tsai, Comparison of different models of latent heat release for modeling casting solidification, AFS Transactions (1990) 539-546.
• [36] C.S. Kantekar, D.M. Stefanescu, Macro-micro modeling of solidification of hypoeutectic and eutectic Al-Si alloys, AFS Transactions 60 (1988) 591-598.
• [37] H. Huang, V.K. Suri, J.L. Hill, J.T. Berry, Heat source/sink algorithm for modeling phase changes durings in castings and water evaporation in green sand molds, AFS Transactions) 54 (1991) 685-689.
• [38] M. Rapaz, Modeling of microstructure formation in solidification processes, International Materials Reviews 34/3(1989) 93-123.
• [39] W. Kurz, D.J. Fisher, Fundamentals of solidification, Trans Tech Publications, U.K.-USA, 1986.
• [40] S. Jeng, S. Chai, Determination of the solidification characteristics of the A356.2 aluminum alloy, Material Science Forum 217-222 (1996) 283-288.
• [41] M. Kiuchi, S. Sigiyama, A new method to detect solid fraction of mushy/semi solid metals and alloys, Annals of the CIRP 43/1 (1994) 271-274.
• [42] N. Saunders, Z. Guo, A.P. Miodownik, J.-Ph. Schillé, Modelling the material properties and behaviour of Ni- and NiFe-based superalloys, Superalloys 718, 625, 706 and Various Derivatives (2006) 571-580.
• [43] K.P. Sołek, R.M. Kuziak, M. Karbowniczek, The application of thermodynamic calculations for the semi-solid processing design, Archives of Metallurgy and Materials 52/1 (2007) 25-32.
• [44] M.B. Djurdjevic, W.T. Kierkus, et al., Modeling of fraction solid for the 319 aluminum alloy, AFS Transactions 14 (1999) 173-179.
• [45] A. Zavaliangos, E. Tzimas, On the approximation of the partial areas method in the calculation of the fraction of solid, Metallurgical and Materials Transactions B-Process Metallurgy and Materials Processing Science 31/4 (2000) 877-879.
• [46] M.B. Djurdjevic, A. Mitrasonovic, J.H. Sokolowski, Development of the Silicon Equivalent (SiEQ) algorithm and its application for calculation of the characteristic temperatures of solidification multi-component 3XX series of Al alloys, Proceedings of the 15th International Conference and Exposition for the Foundry Industry, Monterrey, Mexico, 2003, 214-226.
• [47] F.C.R. Hernandez, M.B. Djurdjevic, W.T. Kierkus, J.H. Sokolowski, Calculation of the liquidus temperature for hypo and hypereutectic aluminum silicon alloys, Materials Science and Engineering A 396/1-2 (2005) 271-276.
• [48] J.L. Murray, A.J. McAlister, The Al-Si (aluminum-silicon) casting system, Bulletin of Alloy Phase Diagrams 5/1 (1984) 74-84.
• [49] W.J. Boettinger, U.R. Kattner, K.W. Moon, J.H. Perepezko, DTA and heat-flux DSC measurements of alloy melting and freezing, NIST Recommended Practice Guide Special Publication 960-15, National Institute of Standards and Technology, Washington, DC, 2006.

専門家Q&A：あなたの疑問に答えます

Q1: なぜこの研究では「動的ベースライン」アプローチが、従来の凝固解析手法より優れているとされているのですか？

A1: 従来のモデル（例：Scheilモデル）は、平衡凝固や固相内での拡散が全くないといった理想的な仮定に基づいているため、実際の非平衡な鋳造プロセスとは乖離がありました。動的ベースラインアプローチは、実際の冷却曲線データから、その材料とプロセス条件に固有の熱損失特性を直接導出します。そのため、仮定に頼らず、より物理的に意味のある、現実に即した固体率の算出が可能になるのです。

Q2: 実験データの信頼性を確保するために、どのような工夫がなされましたか？

A2: データの信頼性を最大限に高めるため、いくつかの工夫が凝らされています。第一に、サンプルの熱容量に対して質量が1%未満の超軽量ステンレス箔カップを使用し、測定系がサンプルの冷却挙動に与える影響を最小化しました。第二に、高感度な熱電対の先端のみを溶湯に直接接触させ、応答遅れをなくしました。最後に、各合金について3回の繰り返し実験を行い、データの再現性を確認しています。

Q3: この手法はAlSiCu合金以外にも適用可能ですか？

A3: はい、適用可能です。論文では、この手法の妥当性を検証するために、高純度のスズやアルミニウムでも実験を行っており、非常に高い精度でベースラインを決定できることを示しています。動的ベースラインアプローチの基本原理は、材料の熱物性値に依存しないため、アルミニウム合金だけでなく、鉄合金や銅合金など、あらゆる金属・合金の凝固解析に応用できる普遍性を持っています。

Q4: 論文で言及されている「シリコン当量（SiEQ）」とは何ですか？ なぜこれを使用するのですか？

A4: シリコン当量（SiEQ）とは、Al-Si二元合金を基準として、他の添加元素（この研究ではCu、Fe、Mgなど）が凝固温度に与える影響を、等価なシリコン濃度に換算するための指標です。多成分の複雑な合金系を、SiEQという単一の変数で整理することで、化学組成と凝固特性との関係性をよりシンプルに、かつ明確に分析することが可能になります。

Q5: 冷却速度は固体率の推移に影響しますか？

A5: はい、影響します。論文のFigure 14では、ほぼ同じ純度のアルミニウムでも、冷却速度が異なると（本研究の1.6℃/sに対し、参考文献[25]では3.0℃/s）、凝固の開始点と終了点で固体率の推移に明確な違いが現れることを示しています。これは、冷却速度が過冷度や組織の微細さに影響を与えるためです。本研究の動的ベースラインアプローチは、特定の冷却条件下での凝固挙動をそのまま捉えるため、こうしたプロセスの影響を評価する上でも有効です。

結論：より高い品質と生産性への道を拓く

鋳造シミュレーションの精度不足という長年の課題に対し、本研究は「動的ベースラインアプローチ」という強力な解決策を提示しました。この手法により、AlSiCu合金の凝固解析の精度は飛躍的に向上し、化学成分から凝固挙動を予測する信頼性の高いモデルが構築されました。これは、R&D部門にとっては合金開発の加速を、製造部門にとってはプロセスの最適化と欠陥の低減を意味します。

CASTMANでは、こうした最新の業界研究を応用し、お客様の生産性と品質の向上を支援することをお約束します。本稿で議論された課題がお客様の事業目標と合致する場合、ぜひ弊社のエンジニアリングチームにご相談ください。これらの原理をお客様の部品にどのように実装できるか、共に探求してまいります。

著作権情報

このコンテンツは、P. Marchwica, J.H. Sokolowski, W.T. Kierkusによる論文「Fraction solid evolution characteristics of AlSiCu alloys - dynamic baseline approach」に基づく要約および分析です。

Source: https://www.journalamme.org/papers_vol47_2/4721.pdf

この資料は情報提供のみを目的としています。無断での商業利用は禁じられています。 Copyright © 2025 CASTMAN. All rights reserved.