Towards Location Specific Statistical Fracture Prediction in High Pressure Die Castings
この技術概要は、[R. Watson, W.D. Griffiths, T. Zeguer, S. Ruffle]によって執筆され、[10th European LS-DYNA Conference 2015]で発表された学術論文「[Towards Location Specific Statistical Fracture Prediction in High Pressure Die Castings]」に基づいています。

キーワード
- 主要キーワード: 高圧ダイカスト 破壊予測
- 副次キーワード: 欠陥予測, 強度分布, LS-DYNA, 引張試験, 湯流れシミュレーション, 軽量化
エグゼクティブサマリー
- 課題: 高圧ダイカスト(HPDC)部品は、鋳造プロセス中に巻き込まれる欠陥によって強度がばらつくため、過度に安全側な(重い)設計になりがちです。
- 手法: 鋳造シミュレーションによる欠陥分布予測と、引張試験による実測強度データを、独自のファジー統計相関法を用いて関連付けました。
- 主要なブレークスルー: 部品全体の均一な強度ではなく、部品内の「場所ごと」の統計的な強度分布を予測し、それをLS-DYNAの破壊シミュレーションモデルに直接マッピングする手法を実証しました。
- 結論: この手法により、鋳造部品の信頼性をより正確に予測し、設計を最適化して軽量化を実現する道が開かれます。
課題:なぜこの研究がHPDC専門家にとって重要なのか
高圧ダイカストは、複雑形状のアルミニウム部品を大量生産できる経済的な製法です。しかし、溶融金属が高速で金型に充填される際、空気や酸化膜が巻き込まれて「巻き込み欠陥」を形成します。これらの欠陥は、製品の強度を著しく低下させる原因となります。
問題は、これらの欠陥がどこに、どれくらいの大きさで発生するかが予測困難なため、部品の強度が大きくばらつくことです。このため、設計エンジニアは最悪のケースを想定し、部品全体に対して保守的な(低い)強度推定値を用いて設計せざるを得ませんでした。その結果、部品は本来必要とされる以上に重くなり、軽量化のポテンシャルを十分に活かせないという課題がありました。この研究は、この「強度の不確実性」という長年の課題に正面から取り組むものです。
アプローチ:研究手法の解明
本研究では、シミュレーションと実測データを組み合わせた複合的なアプローチにより、鋳造部品の局所的な強度を予測する手法を検証しました。
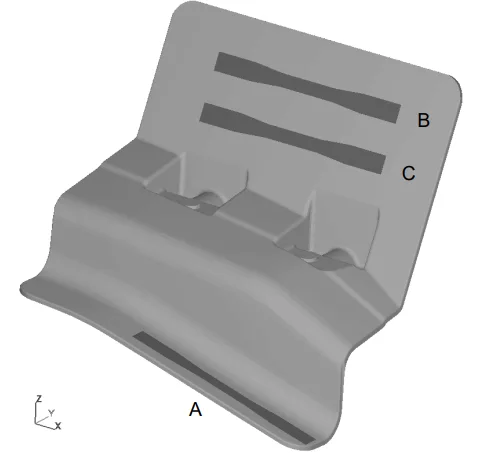
手法1:鋳造と引張試験 実際の製造プロセスを模倣し、商業用部品に対して2種類の鋳造条件(「フルゲート」と「ブランクゲート」)を設定して試験鋳造を行いました。各鋳造品から特定の3つの部位(A, B, C)から引張試験片を切り出し、引張試験を実施して実際の破壊強度データを収集しました。
手法2:鋳造シミュレーションによる欠陥予測 CFDソフトウェア「FLOW-3D」と、独自に開発された「表面積巻き込みコード(Surface Area Entrainment Code)」を用いて、2つの鋳造プロセスの湯流れをシミュレーションしました。このシミュレーションにより、巻き込み欠陥(ラグランジュ粒子としてモデル化)が鋳造プロセス中にどこで生成され、最終的に製品内のどこに分布するかを予測しました。
手法3:統計的マッピングとLS-DYNAへの統合 シミュレーションで得られた局所的な欠陥密度分布と、引張試験で得られた実測の強度分布(ワイブル分布で整理)との間に、逆べき乗則の関係を仮定して統計的な関連付けを行いました。この相関関係を用いて、部品内の各要素(メッシュ)に対応する統計的な強度分布を生成し、PRIMERスクリプトを介してLS-DYNAの構造解析モデルにマッピングしました。これにより、不均一な強度分布を持つ材料モデルが作成されました。
ブレークスルー:主要な研究結果とデータ
本研究は、シミュレーションによる強度予測の精度と実用性を実証する、いくつかの重要な結果を明らかにしました。
発見1:鋳造プロセスの違いが欠陥分布に与える影響を正確に予測
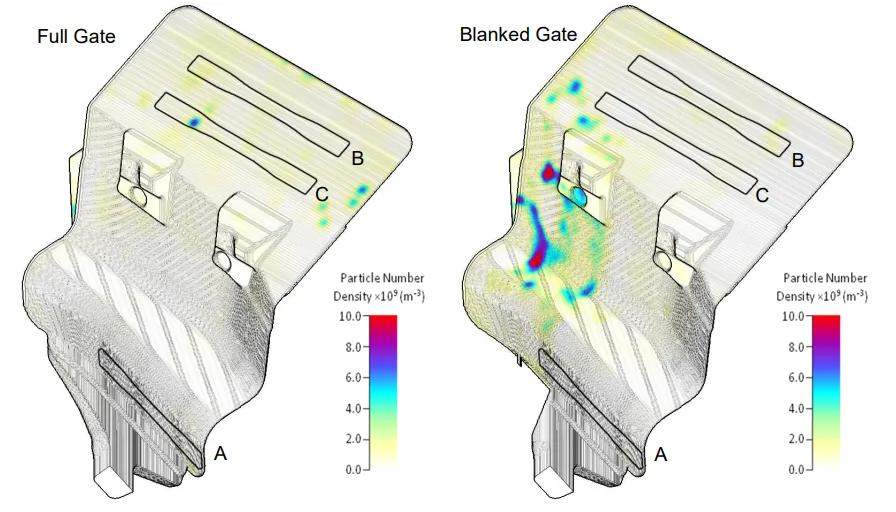
シミュレーションは、2つの鋳造条件(フルゲートとブランクゲート)が欠陥の最終的な分布に大きく異なる影響を与えることを明確に示しました。図3に示すように、「ブランクゲート」ケースでは、特定の領域に欠陥が高密度で集中していることが予測されており、これは湯流れが大きく変更されたことを反映しています。この結果は、シミュレーションがプロセスの変更に起因する欠陥分布の変化を捉える能力を持つことを示しています。
発見2:LS-DYNAモデル内での不均一な強度分布の可視化
開発されたマッピング手法により、引張試験片のLS-DYNAモデル内に統計的な強度分布を割り当てることに成功しました。図4は、そのマッピング結果の例を示しており、強度が赤色(例:200 MPa)から黄色(例:300 MPa)の間の色で可視化されています。これにより、試験片内でも強度が均一ではなく、場所によって高い領域や低い領域が存在する、より現実的な材料モデルが構築できることが実証されました。
発見3:シミュレーションによる破壊予測と実験データとの高い一致
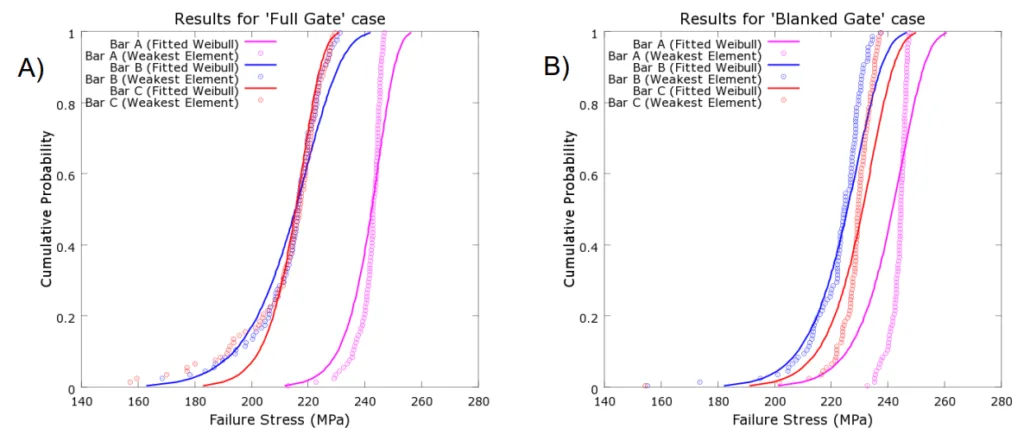
強度分布をマッピングしたLS-DYNAモデルを用いて破壊シミュレーションを繰り返し実行し、その結果を実験データから得られたワイブル分布と比較しました。図5に示すように、シミュレーションから得られた破壊応力の累積分布は、特に強度の低い側(設計上最も重要な領域)において、実験データと非常によく一致しました。これは、本手法が鋳造品の破壊挙動を高い忠実度で再現できることを検証するものです。
研究開発および製造現場への実践的な示唆
- プロセスエンジニアへ: この研究は、ゲート設計などのプロセスパラメータの変更が、製品内のどの部分の欠陥密度を高め、強度を低下させるかをシミュレーションで予測できることを示唆しています。これにより、製造プロセスの最適化をより科学的に進めることが可能になります。
- 品質管理チームへ: 図5のデータは、製品の強度が単一の値ではなく、統計的な分布を持つことを明確に示しています。この知見は、単なる合否判定を超えて、製品の信頼性を確率的に評価する新しい品質保証基準の策定に役立つ可能性があります。
- 設計エンジニアへ: この研究の最大の成果は、部品内の場所に応じた強度(局所的な材料特性)を考慮して設計できる可能性を示したことです。これにより、応力集中部には高い強度を確保しつつ、他の部分では材料を削減するなど、より高度な軽量化設計が実現可能になります。
論文詳細
高圧ダイカストにおける局所的な統計的破壊予測に向けて
1. 概要:
- タイトル: Towards Location Specific Statistical Fracture Prediction in High Pressure Die Castings
- 著者: R. Watson¹, W.D. Griffiths¹, T. Zeguer², S. Ruffle³
- 発行年: 2015
- 発表学会/ジャーナル: 10th European LS-DYNA Conference 2015, Würzburg, Germany
- キーワード: 高圧ダイカスト, 巻き込み欠陥, 統計的破壊予測, ワイブル分布, LS-DYNA, 鋳造シミュレーション
2. 抄録:
高圧ダイカストは、高い生産量でアルミニウム部品を製造する経済的な手段であり、その設計自由度から鍛造組立品と比較してより軽量な構造の構想を可能にする。しかし、鋳造アルミニウム部品は、鋳造プロセス中の空気の巻き込みによって引き起こされる欠陥による損傷に対して脆弱であることが示されている。 最近開発された巻き込み予測アルゴリズムは、鋳物内の巻き込み欠陥の分布をより定量的に予測すると考えられており、これを用いて商業部品の2つの鋳造プロセスバリアントにおけるこれらの欠陥の分布を予測した。新しいファジー統計相関法を用いて、予測された巻き込み損傷の分布を、引張試験によって決定された巻き込み損傷の統計的分布と相関させた。 本研究は、相関付けられた強度分布を相関に使用された試験片のLS-DYNAモデルにマッピングするマッピング方法論の検証を示す。結果は、ファジー統計的巻き込み損傷モデルが引張試験データに厳密に適合できること、そしてこの忠実度が記述された方法を用いてLS-DYNAシミュレーションで再現できることを示したが、この方法の予測能力を実証するにはさらなる作業が必要である。
3. 序論:
高圧ダイカストは、自動車産業で広く使用されている。比較的複雑な形状で設計でき、大量生産が低コストで可能だからである。しかし、その強度に影響を与える要因を考慮することが困難なため、しばしば保守的な強度推定に基づいて設計される。これらの要因の一つが、各鋳物内に特有の巻き込み欠陥の分布である。本研究の目的は、鋳造アルミニウム部品における巻き込み欠陥の性質に関する最近の開発と洞察を要約し、実証することである。この新しい理解を数理モデルに組み込むことで、鋳造部品内の統計的な強度分布のマップを生成することができる。この強度分布は、鋳造プロセスのシミュレーションによって予測された巻き込み欠陥の分布に基づいており、さらに部品の破壊をシミュレートするためにLS-DYNAキーファイルにマッピングすることができる。
4. 研究の概要:
研究トピックの背景: 高圧ダイカスト(HPDC)部品は、その経済性と設計自由度から広く利用されているが、鋳造プロセス中に発生する空気や酸化膜の巻き込みに起因する内部欠陥により、機械的特性、特に強度がばらつくという問題を抱えている。これにより、設計者は部品の信頼性を確保するために保守的な設計を強いられ、軽量化のポテンシャルを十分に引き出せていない。
従来研究の状況: 従来、鋳造欠陥の予測には「空気接触時間」などのスカラー輸送モデルが用いられてきたが、これらは欠陥がどこで生成されるかを示すものの、最終的にどこに分布するかを動的に追跡するには限界があった。その後、BOEC(Boolean Oxide Entrainment Code)や本研究で用いられたSAE(Surface Area Entrainment Code)のようなラグランジュ粒子追跡法が開発され、より物理的に現実に近い欠陥輸送のモデル化が可能になった。しかし、シミュレーションで予測された欠陥分布を、部品の局所的な機械的強度の統計的分布に定量的に結びつける包括的な方法論は確立されていなかった。
研究の目的: 本研究の目的は、鋳造シミュレーションによって予測された巻き込み欠陥の分布に基づき、鋳造部品内の局所的な統計的強度分布マップを生成し、そのマップをLS-DYNAの有限要素モデルに適用して部品の破壊をシミュレートする一連の方法論を実証し、検証することである。
中心的な研究: 本研究では、2つの異なる鋳造プロセス(「フルゲート」と「ブランクゲート」)で製造された商業用HPDC部品を対象とした。まず、FLOW-3Dを用いた鋳造シミュレーションにより、各プロセスの欠陥分布を予測した。次に、実際の鋳造品から切り出した試験片で引張試験を行い、破壊強度の統計的データ(ワイブル分布)を取得した。そして、シミュレーションによる欠陥密度と実験による強度分布との間に統計的な相関関係を構築する「ファジー統計相関法」を開発・適用した。最終段階として、この相関関係を用いて生成された強度分布マップを試験片のLS-DYNAモデルにマッピングし、破壊シミュレーションの結果が実験データと一致するかを比較することで、提案された方法論全体の妥当性を検証した。
5. 研究方法論
研究デザイン: 本研究は、計算シミュレーションと物理実験を組み合わせた検証的アプローチを採用した。商業用HPDC部品について、2つの鋳造プロセスバリアント(「フルゲート」と「ブランクゲート」)を設定し、それぞれの条件で鋳造を行った。各鋳造品から3つの特定の位置(A, B, C)から引張試験片を抽出し、実験データとシミュレーション結果を比較した。
データ収集と分析方法: - 実験データ: 各鋳造品から抽出した試験片に対し、3 mm/minのひずみ速度で単軸引張試験を実施した。得られた試験データから真の破壊応力を算出し、最尤推定法(MLE)を用いて2パラメータ・ワイブル分布で特性評価した。 - シミュレーションデータ: 商業用CFDパッケージ「FLOW-3D」と、ユーザーサブルーチンとして組み込まれた「表面積巻き込みコード(SAE Code)」を使用して鋳造プロセスをシミュレーションした。巻き込み欠陥はラグランジュ粒子としてモデル化され、その最終的な空間分布をデータとして取得した。 - 相関分析: シミュレーション結果の欠陥密度をサンプリングするためにランダムウォークアルゴリズムを開発し、そのサンプルデータを3パラメータ・フレシェ分布に適合させた。欠陥密度(損傷)と真の破壊応力(強度)の関係は、逆べき乗則(σF = A·D^B)を仮定し、最小二乗法を用いてパラメータを較正した。 - LS-DYNAへのマッピング: 最適化されたマッピングパラメータを用いて、PRIMERスクリプトによりLS-DYNAモデル内の各要素に強度分布を割り当てた。強度のばらつきをモデル化するため、要素を強度ごとに複数のビンにグループ化し、各ビンにユニークなPART IDと材料特性(MAT_ADD_EROSION)を割り当てる手法を用いた。
研究対象と範囲: 本研究は、アルミニウム高圧ダイカスト部品を対象とする。研究の範囲は、鋳造シミュレーションによる巻き込み欠陥の分布予測、実験的な引張強度データとの統計的相関付け、そしてその相関関係をLS-DYNAの破壊シミュレーションにマッピングする方法論の検証に限定される。方法論の予測能力そのものを完全に実証するには、さらなる研究が必要であるとされている。
6. 主要な結果:
主要な結果: - 流体シミュレーションは、「フルゲート」と「ブランクゲート」のケースで、予測される欠陥の幾何学的分布が著しく異なることを示した(図3)。これは、ゲートの一部を塞ぐことが流体の流れと欠陥分布に大きな影響を与えたことを示している。 - マッピングプロセスにより、各試験片のLS-DYNAモデル内に不均一な強度分布が生成された(図4)。これにより、一部の領域は他の領域よりも均一な強度を持ち、また全体的に強度がより高い、あるいは低い領域が存在することが視覚的に示された。 - 強度分布をマッピングしたLS-DYNAモデルを100回実行して得られた破壊応力の累積分布は、マッピングパラメータの基になった実験的なワイブル分布と、特に各曲線の中心部分で非常によく一致した(図5)。この忠実度は、試験片位置Bに関する両データセットの低い側の裾野(lower tail)でも維持された。
Figure Name List:
- Fig.1: An SEM image of an air-pore (A, right), associated with a region of micro-shrinkage porosity (A, left), alongside with a higher magnification view of the air-pore (B), showing the location that the EDX spectrum (C) was sampled from.
- Fig.2: The locations on the trial castings where the test bars were extracted from.
- Fig.3: Final time frame of "Full Gate” and “Blanked Gate" simulations, coloured by defect number density, with test bar positions overlaid.
- Fig.4: Example strength mappings of each test bar.
- Fig.5: A comparison of the cumulative distributions of true fracture stress produced by repeated evaluation of the defect mapping algorithm, and the Weibull statistics that the mapping parameters are based on.
7. 結論:
提示された結果は、流体シミュレーションで使用された欠陥予測アルゴリズムが、十分に現実的な欠陥分布を生成できることを示している。この分布は、合理的に良好な適合度を持つ統計的損傷関数と相関させることができるが、各試験片グループ内のばらつきは一貫して過小評価されており、特に各分布の上側の裾野(upper tail)に向かってその傾向が強い。もし低い側の裾野が過小評価された結果が設計に使用された場合、部品の耐久性が不足する可能性がある。 さらに、マッピング方法論自体が、マッピングされた各試験片内で信頼できる強度分布を生成することが示された。詳細なマッピング方法論の使用は、引張試験で破壊しなかった領域の強度について、おそらく最良の指標を与える。 図6(※本文中では図5を指していると思われる)は、マッピングがフレシェ型分布の負のべき乗に基づいているため、予想通りマッピングされた強度分布に明確な上限があることを示している。現在のほとんどのケースでは、これは最も強い試験片の強度が過小評価されることを意味する。しかし、この特徴の利点は、要素がより小さな体積にスケーリングされるにつれて、その強度が非現実的なほど高くならないことである。 ここで提示された方法論のもう一つの潜在的な利点は、統計データをLS-DYNAシミュレーションにマッピングするプロセスがPRIMERスクリプトを使用して行われることであり、これは商業的な環境で比較的容易に実装できる。
8. 参考文献:
- [1] Campbell, J: "Castings", 1, 1991
- [2] Campbell, J: "Complete Casting Handbook", issue 1, 2011
- [3] Green, N; Campbell, J: "Statistical distributions of cast Al-7Si-Mg alloy", Materials Science and Engineering A, v. 173, 1993, pp. 261-266
- [4] Weibull, W: “A Statistical Distribution of Wide Applicability", Journal of Applied Mechanics, v. 13, 1951, pp. 293–97
- [5] Nyahumwa, C: “Influence of Oxide Film Filling Defects on Fatigue Properties of Cast Al-7Si-Mg Alloy", PhD Thesis, University of Birmingham, 1997
- [6] Tiryakioğlu, M: “On the size distribution of fracture-initiating defects in Al- and Mg-alloy castings", Materials Science and Engineering A, v. 476, 2008, pp. 174-177
- [7] Chakrabarty, J: “Applied Plasticity, Second Edition", 1, 2010, p. 7
- [8] Dørum, C; Laukli, H; Hopperstad, O-S: “Through Process numerical simulations of the structural behaviour of Al-Si die-castings", Computational Materials Sceince, v. 46, 2009, pp. 100-111
- [9] Reilly, C: "Development Of Quantitative Casting Quality Assessment Criteria Using Process Modelling", PhD Thesis, University of Birmingham, 2010
- [10] Yue, Y; Green, N R: “Modelling of different entrainment mechanisms and their influences on the mechanical reliability of Al-Si castings", IOP Conf. Series: Materials Science and Engineering, v. 33, 2012, 012072
- [11] Watson, R; Zeguer, T; Ruffle, S; Griffiths, W D: "Application of a Novel Entrainment Defect Model to a High Pressure Die Casting", Advanced Materials Research, THERMEC 2013 Supplement, pp. 801-806
専門家Q&A:あなたの疑問に答えます
Q1: なぜ単純な欠陥の数ではなく、統計的なアプローチが必要だったのですか?
A1: 鋳造プロセスには乱流やプロセス条件のわずかな変動が伴うため、全く同じ鋳造品は二つと存在しません。論文で示されているように、このばらつきは強度のばらつきに直結します。統計的アプローチ(ワイブル分布やフレシェ分布など)を用いることで、この固有のばらつきをモデル化し、単一の決定論的な値ではなく、確率的な強度分布として評価することが可能になります。これにより、より現実的で信頼性の高い破壊予測が実現できます。
Q2: このモデルでフレシェ分布が重要な役割を果たしているのはなぜですか?
A2: フレシェ分布は、ワイブル分布やガンベル分布と並ぶ極値分布の一種です。論文では、欠陥の損傷能力をモデル化するために使用されています。その利点は、強度のワイブル分布と逆べき乗則を介して数学的に密接に関連付けられる点にあります。この逆べき乗則は、破壊力学における破壊応力と亀裂長さの関係式(グリフィス理論など)とも類似しており、物理的な妥当性を持つモデル構築に貢献しています。
Q3: この手法は、「空気接触時間」のような従来の欠陥予測モデルと比べて、どのように優れているのですか?
A3: 「空気接触時間」のような従来のスカラーモデルは、溶湯がどれくらいの時間空気に触れていたかを示すだけで、欠陥が最終的にどこへ運ばれるかを正確に追跡できませんでした。本研究で用いられた手法(SAEコード)は、欠陥を個別のラグランジュ粒子としてモデル化し、湯流れに乗って輸送される様子を追跡します。これにより、欠陥がどこで「生成」されるかだけでなく、最終的に製品内のどこに「分布」するかを、より物理的に忠実に予測できる点が大きな進歩です。
Q4: 論文では、強度分布の上側(最も強い部分)が過小評価される傾向があると述べられていますが、これは設計上どのような意味を持ちますか?
A4: 設計において最も危険なのは、強度の下限(最も弱い部分)を過大評価し、実際よりも強いと判断してしまうことです。このモデルは、強度の下限については実験データとよく一致する一方で、上限を過小評価する傾向があります。これは、最も強いサンプルのポテンシャルを完全には捉えきれていないことを意味しますが、設計の観点からは「安全側」の予測となります。つまり、このモデルに基づいて設計された部品は、予期せぬ破壊を起こすリスクが低く、保守的で安全な設計に繋がります。
Q5: この方法論を実際の製品開発ワークフローに導入するには、具体的にどのような手順が必要ですか? A5: この方法論は、複数のソフトウェアとプロセスを連携させることで実現されます。まず、FLOW-3DのようなCFDソフトウェアで鋳造プロセスをシミュレーションし、欠陥の分布データを生成します。次に、論文で提案された統計アルゴリズム(ランダムウォークや逆べき乗則フィッティングなど)を用いて、欠陥データを強度データに変換します。最後に、PRIMERのようなプリプロセッサ用のスクリプトを用いて、この局所的な強度分布データをLS-DYNAのFEAモデルにマッピングし、破壊解析を実行します。
結論:より高い品質と生産性への道を開く
高圧ダイカスト部品の強度ばらつきという長年の課題に対し、本研究は「局所的な統計的破壊予測」という強力な解決策を提示しました。鋳造シミュレーションと実測データを高度に連携させることで、部品内の強度分布を正確にマッピングし、より信頼性の高い破壊シミュレーションを可能にしました。このブレークスルーは、R&Dおよび製造オペレーションにおいて、より軽量で信頼性の高い部品設計を加速させます。
CASTMANでは、このような最新の業界研究を応用し、お客様の生産性と品質向上を支援することにコミットしています。本稿で議論された課題がお客様の事業目標と合致する場合、ぜひ当社のエンジニアリングチームにご相談ください。これらの原理をお客様のコンポーネントにどのように実装できるか、共に探求してまいります。
著作権情報
このコンテンツは、"[R. Watson, W.D. Griffiths, T. Zeguer, S. Ruffle]"による論文"[Towards Location Specific Statistical Fracture Prediction in High Pressure Die Castings]"に基づく要約および分析です。
出典: 10th European LS-DYNA Conference 2015, Würzburg, Germany
本資料は情報提供のみを目的としています。無断での商業利用は禁じられています。 Copyright © 2025 CASTMAN. All rights reserved.