電気自動車向け高電圧層状ヒーターの電気-熱-流体シミュレーションによるモデル特性評価

電気自動車向け高電圧層状ヒーターの電気-熱-流体シミュレーションによるモデル特性評価

この紹介論文は、「Energies (MDPI)」によって発行された論文「Model Characterization of High-Voltage Layer Heater for Electric Vehicles through Electro-Thermo-Fluidic Simulations」に基づいています。

1. 概要:

• 論文名: Model Characterization of High-Voltage Layer Heater for Electric Vehicles through Electro-Thermo-Fluidic Simulations
• 著者: Kwon Joong Son
• 発行年: 2024
• 発行学術誌/学会: Energies
• キーワード: high-voltage heater; layer heater; computational fluid dynamics; transient heat transfer; multiphysics; transfer function modeling

2. 要旨:

本稿は、電気自動車（EV）およびプラグインハイブリッド電気自動車（PHEV）を含む環境対応車向けに設計された高電圧層状ヒーター（HVLH）のモデリングと解析に焦点を当てており、電気、熱、流体力学の側面を網羅するマルチフィジックスシミュレーションを通じて行われます。HVLHの製造および実験的特性評価には多大な費用と時間が必要となるため、開発段階ではシミュレーションおよび物理モデリング手法が好まれます。本研究は、電気領域内の発熱体（TFE）の熱境界条件を個別にモデリングする先駆的な試みであり、ジュール加熱の計算と過渡共役熱伝達の解析を可能にします。さらに、本研究はHVLHコンポーネントの伝達関数モデリングの適用を開始し、その用途を暖房、換気、空調（HVAC）システムのより広範な文脈に拡大します。入力電圧と流量条件に基づくジュール加熱と温度場の計算を含むシミュレーション結果は、実験データと密接に一致します。導出された伝達関数は、回帰パラメータとともに、システムの動的挙動を正確に予測します。本研究で提示されたシミュレーションベースのモデリングアプローチは、環境対応の電気暖房システムの設計と制御を大幅に進歩させ、持続可能で費用対効果の高いソリューションを提供します。

3. 序論:

電気自動車（EV）およびプラグインハイブリッド電気自動車（PHEV）は、エンジンや電気モーターからの廃熱を常に利用できるわけではないため、車室内暖房、霜取り、バッテリー予熱のためにバッテリー駆動のヒーターが必要です。高電圧ヒーター（HVH）が一般的に使用され、正温度係数（PTC）ヒーターが一般的なタイプです。PTCヒーターは自己制限的な温度特性を提供しますが、低温で大量の電力を消費し、小型軽量設計の実現には限界があります。本稿は、PTCヒーターの限界に対処するために設計された、銀-パラジウム合金の抵抗層を利用する代替タイプのHVHに焦点を当てています。この高電圧層状ヒーター（HVLH）は熱交換器として機能し、積層された発熱体（TFE）を介して冷却液を加熱します。軽量構造、熱出力と熱交換効率の向上、容易に入手可能な材料の使用による持続可能性の向上、PTCヒーターと比較して初期加温段階で約18%のエネルギー節約の可能性[1]といった利点があります。熱出力は温度センサーとパルス幅変調（PWM）制御によって制御されます。

4. 研究の概要:

研究テーマの背景:

EVやPHEVのような環境対応車には、効率的でコンパクトな暖房システムが必要です。従来のPTCヒーターには欠点があり、銀-パラジウム合金抵抗層（HVLH）を用いたものなど、代替のHVH技術に関する研究が進められています。これらのHVLHは、サイズ、重量、効率、材料の持続可能性の点で利点があります。

先行研究の状況:

HVLHに関するこれまでの学術研究は、主に流体の流れと熱伝達の数値解析を用いた仮想性能検証と設計最適化に焦点を当てており、多くの場合、定常状態の解析に集中していました[9,10]。著者による以前の研究[11,12]を含むいくつかの研究では、TFE構造のモデリングが改善され、ジュール加熱計算が含まれていました。しかし、これらの先行研究の重大な限界は、定常状態解析に依存していることであり、効果的なコントローラ設計に不可欠な動的挙動や過渡応答を適切に捉えることができません。

研究の目的:

本研究の目的は、HVLHの過渡マルチフィジックス解析を通じて時間応答データを取得し、HVLHの正確な伝達関数モデルを開発することです。このモデルは、HVLHの動的挙動の予測を容易にし、HVACシステムのシステムレベルシミュレーション（例：ModelicaやSimulinkを使用）に統合して、制御戦略を開発・実装することを目的としています。

核心研究:

本研究の核心は、対称的なサーペンタイン流路を特徴とする特定のHVLH設計の包括的な電気-熱-流体シミュレーションです。これには以下が含まれます。

1. 電気領域内における厚膜発熱体（TFE）の熱境界条件の個別モデリング。
2. 印加電圧に基づくジュール加熱の計算。
3. 様々な冷却液流量条件下での過渡共役熱伝達の解析。
4. シミュレートされたステップ応答データからHVLHの動的挙動を特徴付ける伝達関数モデルの導出。

5. 研究方法論

研究設計:

本研究で検討されたHVLHユニットは、以前のヒーターモデル[11]の形状と全体寸法（177.4 mm × 251.0 mm × 20.5 mm）を維持しつつ、対称的なサーペンタイン流路を組み込んでいます。

• 構造: 大量生産向けに設計されており、主要な構造要素はダイカスト可能でボルト締結されます。薄い導電層と絶縁層がアルミニウムカバープレート上にスクリーン印刷され、冷却液の流れを導くサーペンタイン壁と位置合わせされます。
• 発熱体 (TFE): 抵抗発熱層は銀-パラジウム（Ag-Pd）合金（厚さ8 µm）で、上部絶縁層（30 µm）と下部絶縁層（120 µm）の間に挟まれています。これらはアルミナ（Al2O3）で構成されています。TFE構造は、冷却液に浸漬されるのではなく、ヒーターの外面に配置されます。電気接続は、単一の入力端子とスクリーン印刷されたTFE用の接地端子を介して行われます。
• 流路: 単一の円形断面の入口から始まる12本の平行な分岐で構成されています。各分岐は、長方形断面を持つ4重鏡面対称のサーペンタイン経路を有し、カバーを固定するためのボルト穴を挿入するために対称軸近くに機械加工領域を設けています。流路キャビティの体積は183.2 cm³です。
• 材料:
  • ヒーター本体およびカバープレート: Al-Si-Mg系アルミニウム合金（ALDC2）
  • 抵抗発熱体: 銀-パラジウム（Ag-Pd）合金
  • 絶縁層: アルミナ（Al2O3）
  • 冷却液: Table 1に記載の特性。

データ収集・分析方法:

マルチフィジックスシミュレーションは、商用ソフトウェアパッケージCOMSOL Multiphysics 6.0とその補足モジュールであるComposite Materials、AC/DC、CFD、Heat Transferを使用して実施されました。

• 支配方程式とモデル:
  • 流体力学: 定常、非圧縮性、乱流流れは、せん断応力輸送（SST）k-ω乱流モデル（論文中の式(1)および(2)）を用いてモデル化されました。
  • 静電気学とジュール加熱: 電位場Vに対するラプラス方程式∇²V = 0、電界強度E = -∇V、オームの法則J = σE（σは電気伝導率）による電流密度Jの決定、および式(4) Qe = E·Jによるジュール加熱による電力発生。
  • 熱伝達: 導電性Ag-Pd媒体に対する時間依存の電力収支方程式（式(3)）。固体および流体領域間の共役熱伝達（CHT）解析には、[20]で参照されているKays–Crawford乱流プラントル数Prt（式(5)）が採用されました。
• メッシュ生成: 流体および構造固体領域は3D要素を用いて離散化され、薄い複合TFE構造には平面積層シェル要素が使用されました。計算領域の離散化により、合計32,010,895個の3D要素（流体領域に24,856,397個、固体領域に7,154,498個）と、薄膜用に指定された24,704個の積層シェル要素が生成されました。
• 境界条件:
  • 入口および出口パイプの外側円筒面を除くアルミニウム構造の外面は、対流境界条件にさらされました。これらの条件には、5.0 W/m²·Kの対流係数と25 °Cの周囲温度が含まれていました。
  • 入口および出口パイプは、冷却液を運ぶ周囲のプラスチックチューブによって断熱されていると推定されました。
  • 冷却液入口の境界条件は、温度25 °C、流量5、10、15、20 L/min（LPM）で設定されました。
  • 入力電圧は、Figure 2bに示すように、0.01秒で0Vから350Vに滑らかに増加するシグモイド状のステップ信号を生成するように設定されました。
• シミュレーション手順:
  1. 最初に、SST k-ω法を用いた定常状態乱流流れの数値解を導出するためにCFD解析が実施されました。
  2. 次に、電界とジュール加熱の影響を考慮して、60秒間にわたる動的共役熱伝達解析が実行され、データは1秒間隔で記録されました。
• 伝達関数モデリング:
  • HVLHは1次線形時不変（LTI）システムとしてモデル化されました。
  • 1次動的システムのステップ応答の時間領域表現は、式(6) ∆T(t) = (1 - e^(-t/tc)) ∆Tss で表されます。ここで、∆Tは入口から出口までの冷却液温度の上昇を示し、tcは1次LTIシステムの応答速度を定義する時定数です。
  • ステップ応答に対応する伝達関数（TF）は、式(7) TF = ∆T(s)/Vin = KDC / (tcs + 1) で表されます。ここで、∆T(s)は∆T(t)のラプラス変換を表し、Vinは入力電圧の振幅を示し、KDCは直流（DC）ゲインとして定義され、定常状態の温度差とステップ入力振幅の比率を表します（式(8) KDC = ∆Tss / Vin）。
  • KDCとtcは、各流量のシミュレーションデータから決定されました。
  • 伝達関数の2つの主要パラメータ、具体的にはDCゲインKDCと時定数tcと体積流量Qとの間の関数関係を調査するために、Table 2に示されたデータを用いて追加の回帰分析が実施されました。回帰分析のフィッティング曲線は、係数aと定数bで定義される体積流量Qの逆比例関数として選択されました（式(9) f(Q) = a/Q + b）。
  • 最終的な伝達関数は、式(10) TF(s; Q) = 0.2687 / ((1.969Q + 43.68)s + Q) として導出されました。

研究テーマと範囲:

本研究は、電気自動車用高電圧層状ヒーター（HVLH）のモデル特性評価に焦点を当てました。これには以下が含まれます。

• 電気-熱-流体の側面を網羅するマルチフィジックスシミュレーションモデルの開発。
• 異なる冷却液流量（5、10、15、20 LPM）におけるステップ電圧入力下でのHVLHの過渡挙動の解析。
• 電気領域における導電性発熱層を個別にモデル化することによるジュール加熱の計算。
• 過渡共役熱伝達の調査。
• より広範なHVACシステムモデリングおよび制御設計で使用するためのHVLHの伝達関数モデルの導出と検証。

6. 主な結果:

主な結果:

• 流れ場と温度場: シミュレーションにより、5、10、15、20 LPMの4つの異なる流量シナリオにおける定常状態の流れ場、ならびに60秒間の過渡電気場と温度場が得られました。電界はステップ入力印加直後に飽和に達しましたが、温度場は定常状態の挙動に達するまで一定期間過渡応答を示しました。
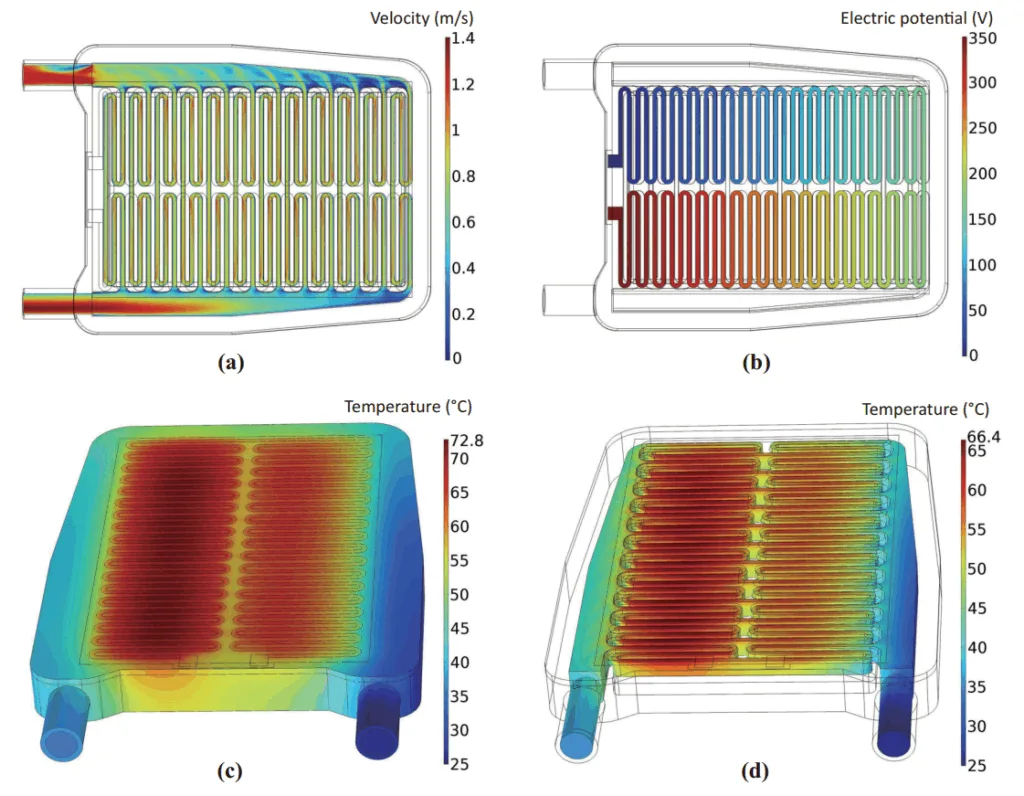
  • 10 LPM（1.67 × 10⁻⁴ m³/sに相当）の流量の場合、60秒時点で、発熱体の最高温度は72.8 °Cに達すると推定されました（Figure 3c）。流体領域の出口断面における平均温度は34.4 °Cと決定され、これは入口温度25 °Cより9.4 °C高い値です（Figure 3d）。Figure 3aは、サーペンタイン流路の中間高さの断面における速度場のカラーコンタープロットを示しています。Figure 3bは、流路壁に沿ってスクリーン印刷されたTFEに350Vのステップ電圧が印加されたときの定常状態の電位場を示しています。
• 過渡熱応答:
  • 入口と出口の間の定常状態の温度差∆Tssは、冷却液流量の増加とともに減少しました（Figure 4a）。
  • 流量が増加すると、∆Tssの初期変化がより急速になり、定常状態に達するまでの時間が短縮されました。
• 実験データとの比較: シミュレートされた∆Tss値は、[28]で引用されている実験データと良好な一致を示し、実験値とシミュレーション値の不一致は1.4%から10.5%の範囲でした（Figure 4b）。
• 伝達関数モデル:
  • HVLHの動的挙動は、1次LTIシステムによって十分に表現されました。
  • 伝達関数パラメータ（DCゲインKDC、時定数tc、立ち上がり時間tr、整定時間ts）は、各流量のシミュレーションデータから導出されました（Table 2）。例えば、
    • 5 LPMの場合: KDC = 0.0537 °C/V, tc = 10.3 s
    • 20 LPMの場合: KDC = 0.0133 °C/V, tc = 3.71 s
  • フィッティングされた伝達関数曲線は、4つの体積流量すべてにおいてシミュレーションデータとよく一致しました（Figure 5）。
  • 回帰分析により、流量Q（LPM）の関数としてKDCとtcの関係が得られました（Figure 6）。
    • KDC(Q) = 0.2687 / Q
    • tc(Q) = 43.68 / Q + 1.696
  • 流量Qを組み込んだ一般化された伝達関数は、TF(s; Q) = 0.2687 / ((1.969Q + 43.68)s + Q)（式(10)）として定式化されました。
  • 導出された伝達関数モデルは、ステップ応答とPWM制御をシミュレートするためのブロック線図で実証され（Figure 7）、システムレベル解析におけるその有用性が強調されました。

図の名称リスト:

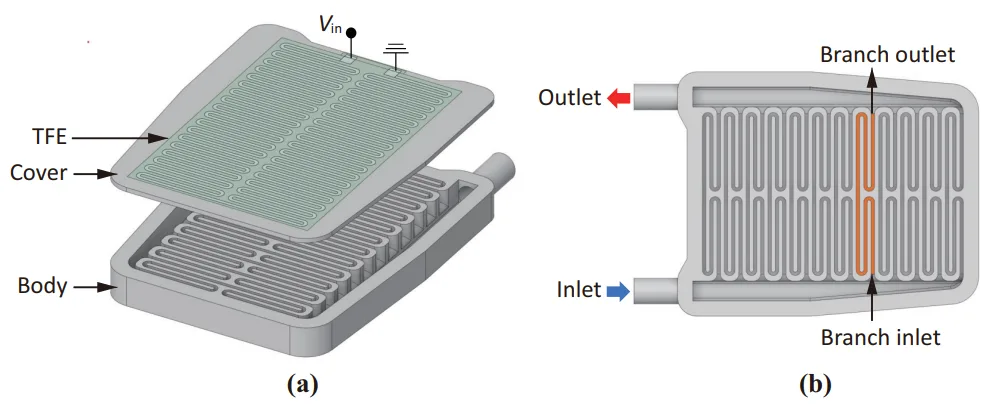
• Figure 1. HVLH schematic diagram: (a) disassembled illustration of heater consisting of main body with serpentine walls and cover plate with screen-printed heating layer; (b) heater body including symmetric serpentine flow channels with twelve branches in parallel.
• Figure 2. Preprocessing of electro-thermo-fluidic simulation: (a) meshed elements zoomed-in around the coolant inlet and (b) Sigmoid-based step voltage input function.
• Figure 3. Simulation results for inlet flow rate of 10 LPM at 60 s: (a) steady-state velocity magnitude contour plot at the middle cross-section of serpentine flow channels; (b) electric potential contour plot on the conductive heating layer; (c) temperature contour plot on the solid surface; (d) temperature contour plot on the fluid surface.
• Figure 4. Time-dependent thermal analysis results: (a) temperature difference versus time curve for different coolant flow rates, with data points collected every 2 s; (b) bar graphs comparing simulated and experimental results for steady-state temperature increase from inlet to outlet.
• Figure 5. Transfer function curves fitted against simulation data for various LPMs.
• Figure 6. Results from curve fitting of transfer function parameters for (a) steady-state gain and (b) time constant.
• Figure 7. PWM control of high-voltage heat using the transfer function model: (a) block diagram schematic; (b) step response versus PWM response curves.

7. 結論:

本研究は、高電圧層状ヒーターの過渡電気-熱-流体挙動を特徴付け、正確な伝達関数を導出するための包括的なモデリングおよびシミュレーションアプローチを提示しました。主な成果は以下の通りです。

1. 高度なHVLHモデリング: 本研究は、電気領域内の導電性発熱層を個別にモデリングすることによりHVLHをモデル化およびシミュレートする最初の試みです。これにより、ジュール加熱の計算と過渡共役熱伝達の解析が可能になり、HVLHの熱性能と消費電力の予測精度が向上します。
2. 先駆的な伝達関数開発: 本研究は、HVLHコンポーネントの伝達関数のモデリングにおける先駆的なものであり、システムレベルのHVACモデリングへの統合を可能にします。導出された伝達関数は、電気自動車暖房システムの制御戦略の開発と実装に不可欠です。
3. 高精度なモデル検証: 伝達関数とそのパラメータの回帰分析の結果は、シミュレーションデータを再現する上で高度な精度を示しています。この正確な相関関係は、伝達関数モデルの信頼性と、システムレベルでのHVACの性能予測におけるその将来的な有用性を強調しています。

本研究は、様々なHVACコンテキストに適用可能なモデリングとシミュレーションのための徹底的な方法論を提示することにより、電気自動車の暖房システムの開発と管理を大幅に進歩させます。本研究は、HVLHの設計と強化に貢献するとともに、急成長する電気自動車分野における効果的な暖房ソリューションの広範な採用を促進します。将来の研究の可能性としては、変更された流路とTFE構成を備えた新しいHVLHモデルの開発が挙げられます。さらに、HVLHを含むHVACシステム全体の包括的な動的モデリングと解析を実施して、伝達関数モデルの検証と改善を継続し、現実世界のアプリケーションにおける実用性を高めることが考えられます。

8. 参考文献:

• [1] Li, B.; Kuo, H.; Wang, X.; Chen, Y.; Wang, Y.; Gerada, D.; Worall, S.; Stone, I.; Yan, Y. Thermal Management of Electrified Propulsion System for Low-Carbon Vehicles. Automot. Innov. 2020, 3, 299–316.
• [2] Lei, S.; Xin, S.; Liu, S. Separate and Integrated Thermal Management Solutions for Electric Vehicles: A Review. J. Power Sources 2022, 550, 232133.
• [3] Park, M.H.; Kim, S.C. Heating Performance Characteristics of High-Voltage PTC Heater for an Electric Vehicle. Energies 2017, 10, 1494.
• [4] Park, M.H.; Kim, S.C. Effects of Geometric Parameters and Operating Conditions on the Performance of a High-Voltage PTC Heater for an Electric Vehicle. Appl. Therm. Eng. 2018, 143, 1023–1033.
• [5] Shin, Y.H.; Ahn, S.K.; Kim, S.C. Performance Characteristics of PTC Elements for an Electric Vehicle Heating System. Energies 2016, 9, 813.
• [6] Paunović, V.; Mitić, V.; Đorđević, M.; Prijić, Z. Electrical Properties of Rare Earth Doped BaTiO3 Ceramics. In Proceedings of the 2017 IEEE 30th International Conference on Microelectronics (MIEL), Nis, Serbia, 9–11 October 2017; pp. 183–186.
• [7] Cap, C.; Hainzlmaier, C. Layer Heater for Electric Vehicles. ATZ Worldw. 2013, 115, 16–19.
• [8] Stifel, T. Optimization and Protection of Traction Batteries with an HV Coolant Heater. ATZ Worldw. 2021, 123, 44–47.
• [9] Dong, F.; Feng, Y.; Wang, Z.; Ni, J. Effects on Thermal Performance Enhancement of Pin-Fin Structures for Insulated Gate Bipolar Transistor (IGBT) Cooling in High Voltage Heater System. Int. J. Therm. Sci. 2019, 146, 106106.
• [10] Dong, F.; Wang, Z.; Feng, Y.; Ni, J. Numerical Study on Flow and Heat Transfer Performance of Serpentine Parallel Flow Channels in a High Voltage Heater System. Therm. Sci. 2022, 26, 735–752.
• [11] Son, K.J. Thermo-Fluid Simulation for Flow Channel Design of 7 kW High-Voltage Heater for Electric Vehicles. J. Korea Converg. Soc. 2022, 13, 191–196.
• [12] Son, K.J. Optimal Power Distribution of High-Voltage Coolant Heater for Electric Vehicles through Electro-Thermofluidic Simulations. Int. J. Automot. Technol. 2023, 24, 995–1003.
• [13] Bellocchi, S.; Leo Guizzi, G.; Manno, M.; Salvatori, M.; Zaccagnini, A. Reversible Heat Pump HVAC System with Regenerative Heat Exchanger for Electric Vehicles: Analysis of Its Impact on Driving Range. Appl. Therm. Eng. 2018, 129, 290–305.
• [14] Basciotti, D.; Dvorak, D.; Gellai, I. A Novel Methodology for Evaluating the Impact of Energy Efficiency Measures on the Cabin Thermal Comfort of Electric Vehicles. Energies 2020, 13, 3872.
• [15] Dvorak, D.; Basciotti, D.; Gellai, I. Demand-Based Control Design for Efficient Heat Pump Operation of Electric Vehicles. Energies 2020, 13, 5440.
• [16] Kulkarni, A.; Brandes, G.; Rahman, A.; Paul, S. A Numerical Model to Evaluate the HVAC Power Demand of Electric Vehicles. IEEE Access 2022, 10, 96239–96248.
• [17] Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605.
• [18] Menter, F.R.; Kuntz, M.; Langtry, R. Ten Years of Industrial Experience with the SST Turbulence Model. Turbul. Heat Mass Transf. 2003, 4, 625–632.
• [19] Speziale, C.G.; Abid, R.; Anderson, E.C. Critical Evaluation of Two-Equation Models for near-Wall Turbulence. AIAA J. 1992, 30, 324–331.
• [20] Rivero, E.P.; Granados, P.; Rivera, F.F.; Cruz, M.; González, I. Mass Transfer Modeling and Simulation at a Rotating Cylinder Electrode (RCE) Reactor under Turbulent Flow for Copper Recovery. Chem. Eng. Sci. 2010, 65, 3042–3049.
• [21] Weigand, B.; Ferguson, J.R.; Crawford, M.E. An Extended Kays and Crawford Turbulent Prandtl Number Model. Int. J. Heat Mass Transf. 1997, 40, 4191–4196.
• [22] Luo, D.; Wang, R.; Yan, Y.; Sun, Z.; Zhou, W.; Ding, R. Comparison of Different Fluid-Thermal-Electric Multiphysics Modeling Approaches for Thermoelectric Generator Systems. Renew. Energy 2021, 180, 1266–1277.
• [23] Jouhara, H.; Żabnieńska-Góra, A.; Khordehgah, N.; Doraghi, Q.; Ahmad, L.; Norman, L.; Axcell, B.; Wrobel, L.; Dai, S. Thermoelectric Generator (TEG) Technologies and Applications. Int. J. Thermofluids 2021, 9, 100063.
• [24] Son, K.J. Thermo-Electro-Fluidic Simulation Study of Impact of Blower Motor Heat on Performance of Peltier Cooler for Protective Clothing. Energies 2023, 16, 4052.
• [25] Drumheller, D.S. Hypervelocity Impact of Mixtures. Int. J. Impact Eng. 1987, 5, 261–268.
• [26] Son, K.J.; Fahrenthold, E.P. Impact Dynamics Simulation for Magnetorheological Fluid Saturated Fabric Barriers. J. Comput. Nonlinear Dyn. 2024, 19, 061002.
• [27] Zhang, X.; Jane Wang, Q.; He, T.; Liu, Y.; Li, Z.; Kim, H.J.; Pack, S. Fully Coupled Thermo-Viscoelastic (TVE) Contact Modeling of Layered Materials Considering Frictional and Viscoelastic Heating. Tribol. Int. 2022, 170, 107506.
• [28] Kwon, B.W. Development of 7 kW-Class Thick Film Resistance Heating Electric Heater (10% Weight Reduction) for Lighter Green Vehicle Cooling, Heating and HVAC System; Final Project Report (Written in Korean) No. P0017526; Korean Ministry of Trade, Industry and Energy (MOTIE): Sejong, Republic of Korea, 2023.
• [29] Franlkin, G.F.; Powell, J.D.; Emami-Naeini, A. Feedback Control of Dynamic Systems, 8th ed.; Higher Education, Inc.: Upper Saddle River, NJ, USA, 2018; pp. 137–142.
• [30] Shin, Y.H.; Sim, S.; Kim, S.C. Performance Characteristics of a Modularized and Integrated PTC Heating System for an Electric Vehicle. Energies 2016, 9, 18.

9. 著作権:

• この資料は、「Kwon Joong Son」氏の論文です。「Model Characterization of High-Voltage Layer Heater for Electric Vehicles through Electro-Thermo-Fluidic Simulations」に基づいています。
• 論文の出典: https://doi.org/10.3390/en17122935

この資料は上記の論文に基づいて要約されており、商業目的での無断使用は禁止されています。
Copyright © 2025 CASTMAN. All rights reserved.