鋳造シミュレーション精度を革新する:損傷モデリングへの確率論的アプローチがもたらす信頼性の向上
本技術概要は、Christian Mühlstätter氏が執筆し、8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2018)で発表された学術論文「A Stochastic Approach for Damage Modelling of Cast Alloys」に基づいています。
キーワード
- 主要キーワード: 鋳造合金 損傷モデリング
- 副次キーワード: 確率論的モデリング, 有限要素シミュレーション, 破壊ひずみ, 応力三軸度, アルミニウム鋳造, HPDC
エグゼクティブサマリー
- 課題: 鋳造プロセスに起因する微細組織の不均一性により、従来の決定論的な損傷モデルでは鋳造アルミニウム合金の破壊挙動を正確に予測できませんでした。
- 手法: 様々な応力状態を再現する引張試験を実施し、得られた破壊ひずみのばらつきをコルモゴロフ–スミルノフ検定を用いて統計的に評価し、その確率分布を特定しました。
- 重要なブレークスルー: 鋳造合金の破壊ひずみのばらつきが正規分布に従うことを実証し、これを組み込んだ新しい確率論的損傷モデルのコンセプトを提唱しました。
- 結論: この確率論的アプローチを有限要素シミュレーションに導入することで、鋳造部品の破壊予測の信頼性を大幅に向上させ、より現実的な製品設計と性能評価が可能になります。
課題:なぜこの研究がHPDC専門家にとって重要なのか
自動車産業における軽量化の要求が高まるにつれ、構造部品への鋳造アルミニウム合金の利用が拡大しています。これらの部品の信頼性を保証するためには、有限要素(FE)シミュレーションによる正確な材料挙動の予測が不可欠です。しかし、鋳造プロセスは本質的に、冷却速度や溶湯の流れ、圧力分布などにより、微小な空孔(ボイド)を含む不均一な微細組織を形成します。
従来の損傷モデリング手法(GursonモデルやJohnson-Cookモデルなど)は、材料を均質な連続体として扱うため、このような微細組織のばらつきや、それに起因する機械的特性の空間的な変動を考慮できません。その結果、シミュレーションと実際の製品の破壊挙動との間に乖離が生じ、過剰な安全率を見込んだ設計や、予期せぬ破損リスクという問題に直面していました。この研究は、鋳造合金特有の「ばらつき」を科学的に捉え、シミュレーションの精度を向上させるという、業界が長年抱えてきた課題に取り組むものです。
アプローチ:研究方法の解明
本研究では、鋳造材料の損傷挙動のばらつきを定量的に評価し、モデル化するために、実験と統計解析を組み合わせたアプローチを採用しました。
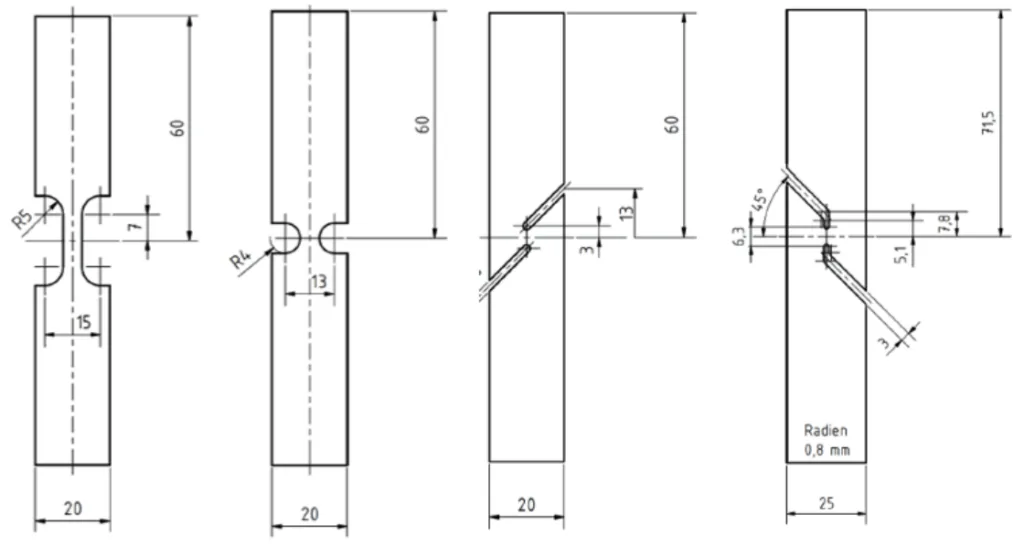
方法1:多様な応力状態の再現 材料の損傷メカニズムは応力状態(特に応力三軸度)に強く依存するため、異なる応力状態を再現できる複数の試験片形状が用いられました。 - 使用した試験片: 平板引張、切欠き、せん断引張、マークラインせん断の4種類の試験片(論文中 Figure 3)がダイカスト製のハット形プロファイルから切り出されました。 - 目的: これらの試験片により、応力三軸度 η = 0(純せん断)から η = 0.57(切欠き引張)までの幅広い応力状態を再現し、それぞれの条件下での破壊挙動データを取得しました。
方法2:実験データの統計的評価 各試験片形状について最低10回の有効な試験を実施し、力-変位曲線を取得しました。特に破壊に至るまでの変位(破壊変位)には、顕著なばらつきが観測されました(論文中 Figure 4, 5)。 - 統計的手法: このデータのばらつきがどのような確率分布に従うかを特定するため、「コルモゴロフ–スミルノフ(KS)検定」と呼ばれる適合度検定が適用されました。KS検定は、サンプル数が比較的少ない場合でも精度の高い結果が得られるため、本研究に適した手法です。
ブレークスルー:主要な研究結果とデータ
本研究は、鋳造合金の損傷挙動のばらつきを統計的にモデル化できることを実証し、シミュレーションの新たな可能性を示しました。
発見1:破壊変位における顕著なばらつきの定量的確認
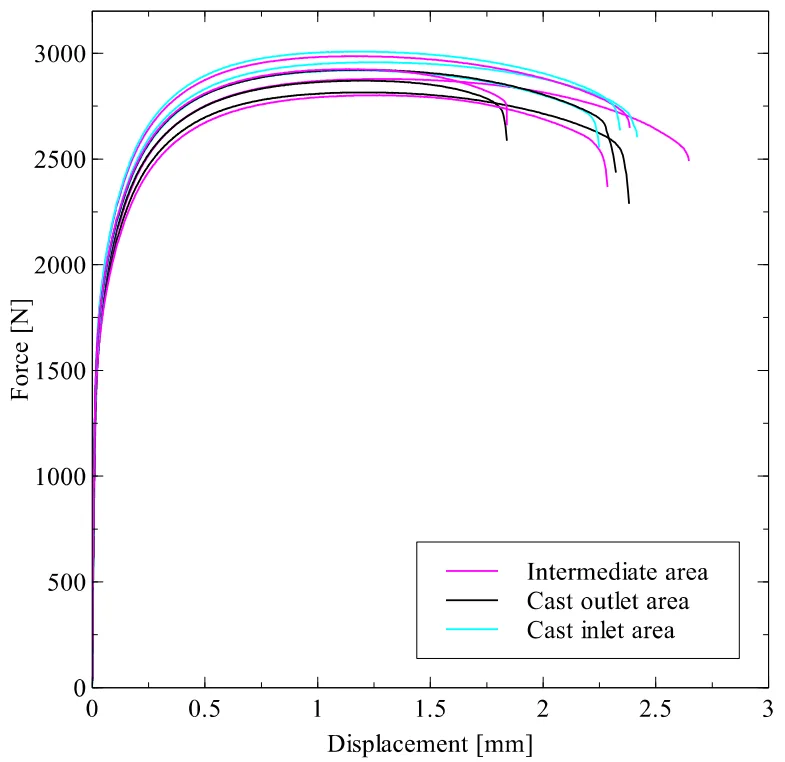
実験結果は、特に応力三軸度が大きい引張試験において、力-変位曲線、とりわけ破壊変位に大きなばらつきがあることを明確に示しました。論文のFigure 4(平板引張試験)では、同じ試験片形状であるにもかかわらず、破壊時の変位が約1.5 mmから2.0 mm超まで、広範囲に分布していることがわかります。これは、従来の平均値のみを扱うモデルでは捉えきれない、鋳造材料固有の不均一性を裏付けるものです。
発見2:破壊ひずみのばらつきは正規分布で記述可能
平板引張試験で得られた破壊ひずみデータにコルモゴロフ–スミルノフ(KS)検定を適用した結果、データが正規分布に従うという仮説(帰無仮説)を棄却できないことが示されました。論文のFigure 6に示されているように、実験データから得られた経験的累積分布関数(黒の階段状の線)は、推定された正規分布の累積分布関数(マゼンタ色の曲線)と非常によく一致しています。これは、破壊ひずみのばらつきがランダムではなく、統計的に予測可能な現象であることを意味します。
発見3:確率論的損傷モデルの新たなコンセプトの提唱
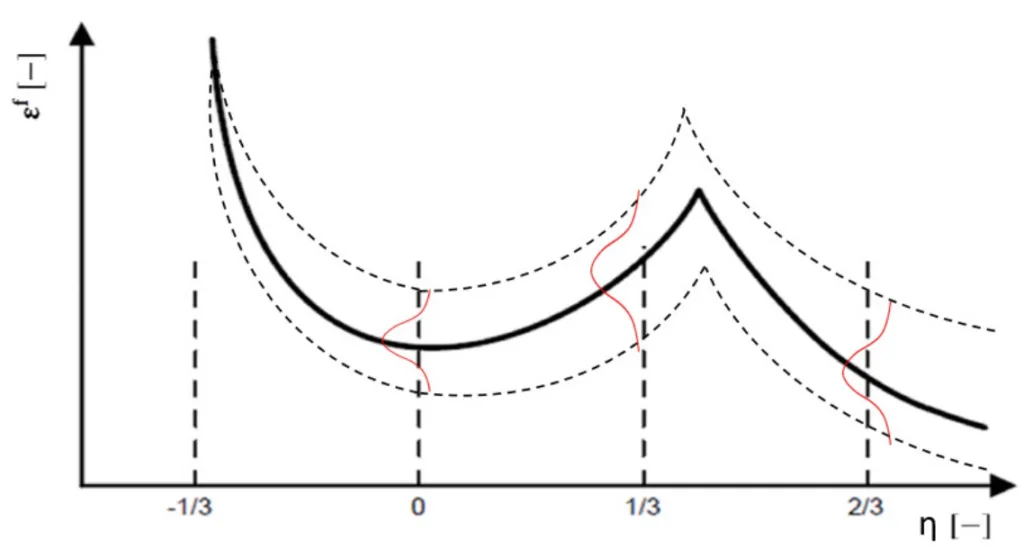
これらの知見に基づき、本研究では従来の決定論的な損傷モデルを発展させた、新しい確率論的損傷モデルのコンセプトを提唱しました(論文中 Figure 7)。これは、応力三軸度(横軸)に対する破壊ひずみ(縦軸)の関係を一本の線(黒の実線)で表すのではなく、各応力三軸度において正規分布(赤のガウス曲線)で表すという考え方です。これにより、シミュレーションにおいて材料特性のばらつきを考慮し、破壊の「確率」を評価することが可能になります。
研究開発および製造現場への実践的示唆
本研究の成果は、鋳造部品の設計、品質管理、製造プロセスの各担当者に、以下のような具体的な指針を提供します。
- プロセスエンジニア向け: 材料特性のばらつきが正規分布で記述できることは、製造プロセスの安定性を統計的に管理する新たな指標となり得ます。例えば、冷却速度や加圧条件といった特定のプロセスパラメータの変動が、破壊ひずみのばらつき(標準偏差)にどう影響するかを分析することで、より安定した品質を実現するプロセス条件の最適化に繋がる可能性があります。
- 品質管理チーム向け: 論文のFigure 4やFigure 6に示されたデータは、従来の合否判定基準に加えて、製品の機械的特性の「ばらつきの許容範囲」を統計的に定義するための基礎情報となります。これにより、より現実的で信頼性の高い品質保証基準を策定することが可能になります。
- 設計エンジニア向け: この確率論的モデルをFEシミュレーションに導入することで、部品が特定の条件下で破壊する「確率」を予測できます。これにより、単に安全率を上乗せするのではなく、信頼性に基づいた最適設計(リライアビリティ設計)が可能となり、過剰品質を避けつつ軽量化と安全性を両立する、より高度な製品開発が実現します。
論文詳細
A Stochastic Approach for Damage Modelling of Cast Alloys
1. 概要:
- Title: A Stochastic Approach for Damage Modelling of Cast Alloys
- Author: Christian Mühlstätter
- Year of publication: 2018
- Journal/academic society of publication: In Proceedings of 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2018)
- Keywords: Damage Modelling, Triaxiality, Goodness-of-fit Test.
2. 抄録:
鋳造アルミニウム合金への関心の高まりは、構造用途における適切なシミュレーションアプローチを要求している。構成挙動に加えて、損傷特性がこの材料にとって重要な役割を果たす。損傷挙動は微細組織に大きく影響される。鋳造微細組織の特異な形態と空孔のランダムな空間的偏差のため、新しい材料モデリングの概念が必要である。本研究では、構造有限要素シミュレーションにおける確率論的な材料キャラクタリゼーションとモデリングの概念が導入される。そのために、実験試験のためのテストマトリックスが議論される。生成された実験データに基づき、適合度検定による確率論的評価が実行される。達成されたキャラクタリゼーションの知見は、アルミニウム鋳造合金の確率論的材料モデリングの概念を導入するために使用される。
3. 序論:
自動車用途における軽量化の要求が高まる中、鋳造アルミニウム合金は構造部品としての重要性を増している。そのため、構造有限要素(FE)シミュレーションにおいて材料挙動を正確に捉えることが必要である。鋳造プロセスにより、材料は特有の形態と微量の空孔を持つようになり、これは時間依存の圧力分布、冷却速度、流動挙動といったプロセスパラメータに大きく影響される。従来のモデリングアプローチ(例:Gurson, 1978; Tvergaard and Needleman, 1984)では、材料は平滑化された微視力学的挙動を持つ連続体と見なされる。また、Wilkinsら(1980)やJohnson and Cook(1985)によって提案された現象論的アプローチは、応力三軸度に依存する破壊ひずみによって材料損傷を記述するが、これらのモデルの標準的な実装も平滑化されており、材料パラメータの空間的変動を考慮していない。本稿では、鋳造材料のキャラクタリゼーションとモデリングのための確率論的考察の概念と組み合わせた現象論的アプローチを導入する。
4. 研究の概要:
研究トピックの背景:
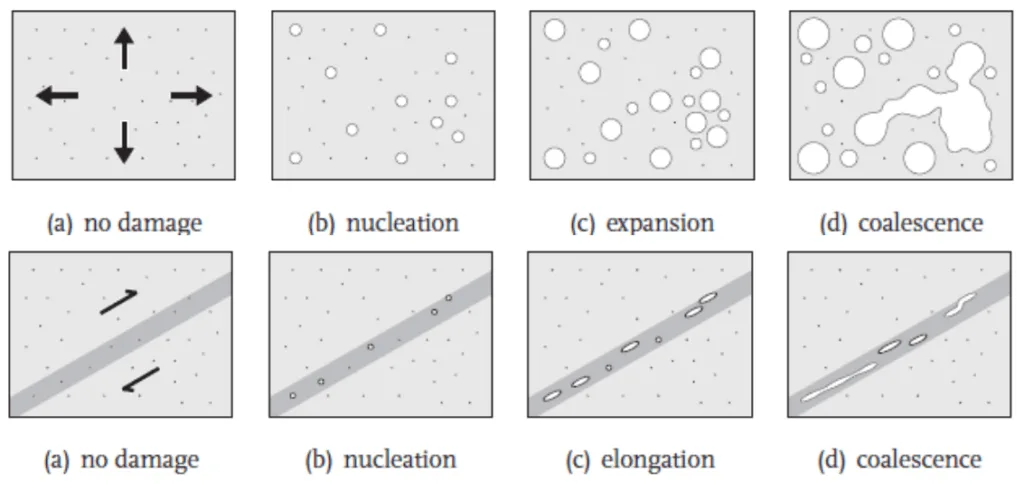
金属材料の延性破壊は、材料内部の微小な空孔の発生、成長、合体といった微視力学的現象の進展によって構成される。この破壊挙動は、材料が置かれている応力状態、特に静水圧応力とフォン・ミーゼス相当応力の比で定義される応力三軸度(stress triaxiality)に強く依存する。
先行研究の状況:
最先端の損傷モデリングは、Bao and Wierzbicki (2004) のアプローチに基づいている。このアプローチでは、特性的な破壊ひずみが応力三軸度の関数として定義される。しかし、このモデルや他の従来モデルは、鋳造合金に見られる微細組織の不均一性やそれに伴う機械的特性のばらつきを考慮していない決定論的な(deterministic)手法である。
研究の目的:
本研究の目的は、鋳造アルミニウム合金の損傷挙動に見られるばらつきを考慮するため、確率論的な材料キャラクタリゼーションとモデリングの概念を導入することである。これにより、従来の平滑化されたモデルよりも現実に即したシミュレーションの実現を目指す。
研究の核心:
本研究の核心は、実験的に得られた破壊ひずみデータのばらつきを、適合度検定を用いて統計的に評価し、その結果に基づいて確率論的な損傷モデルの概念を構築することにある。具体的には、破壊ひずみを単一の値ではなく確率変数として扱い、その確率分布を特定することで、シミュレーションにおける材料特性のばらつきを再現する。
5. 研究方法
研究デザイン:
本研究は、実験的キャラクタリゼーションと統計的データ解析を組み合わせたアプローチを採用した。ダイカスト製アルミニウム合金から複数の形状の試験片(平板引張、切欠き、せん断引張、マークラインせん断)を切り出し、引張試験を実施した。これにより、異なる応力三軸度状態における材料の損傷挙動を体系的に調査した。
データ収集と分析方法:
各試験で力-変位曲線を取得し、特に破壊に至る変位の値を抽出した。収集された離散的な破壊変位データに対して、コルモゴロフ–スミルノフ(KS)検定を適用した。この適合度検定により、実験データのばらつきが正規分布などの特定の確率分布にどの程度従うかを定量的に評価した。
研究対象と範囲:
研究対象は、安定した定常状態で製造されたダイカスト製アルミニウム合金である。本研究は、延性破壊における破壊変位のばらつきに焦点を当て、その確率論的キャラクタリゼーションと、現象論的損傷モデルへの統合コンセプトの提案を範囲とする。
6. 主要な結果:
主要な結果:
- 実験で得られた力-変位曲線は、特に平板引張試験(Figure 4)において、破壊変位に顕著なばらつきを示した。マークラインせん断試験(Figure 5)でもばらつきは見られたが、引張試験よりも小さかった。
- 平板引張試験のデータにコルモゴロフ–スミルノフ(KS)検定を適用した結果、パラメータTの値が0.139となり、帰無仮説の棄却条件である0.41を下回った。これにより、実験データが正規分布に従うという帰無仮説は真であると結論付けられた。
- Figure 6は、実験データから得られた経験的累積分布関数と、推定された正規分布の累積分布関数がよく一致していることを視覚的に示している。
- 以上の結果に基づき、従来のBao-Wierzbickiモデル(決定論的な曲線)に、各応力三軸度における破壊ひずみの確率分布(ガウス曲線として模式的に表示)を組み合わせた、確率論的損傷モデルの概念が提案された(Figure 7)。
Figure Name List:
- Figure 1: Evolution of material damage by different stress states (Engelen, 2005).
- Figure 2: Characteristic metal fracture strain curve as function of the stress triaxiality (Bao and Wierzbicki, 2004).
- Figure 3: Test geometries for characterisation of the damage behaviour (from left: flat tensile, notched, shear tensile and Merklein shear).
- Figure 4: Experimental force vs. displacement curves of flat tensile tests for different regions within the casted part.
- Figure 5: Experimental force vs. displacement curves of Merklein test geometry for different regions within the casted part.
- Figure 6: Visual representation of the Kolmogorov-Smirnov goodness-of-fit test with normal distribution and empirical CDF for tensile test data.
- Figure 7: Schematic concept for the stochastic damage modelling (red and dashed line) based on the approach of (Bao and Wierzbicki, 2004) (black, solid line).
7. 結論:
応力三軸度の関数としての破壊ひずみを考慮した損傷モデリングは、確立された手法である。しかし、鋳造アルミニウム合金においては、不均一な材料・損傷挙動が無視されている。本稿で導入された概念は、この欠点を克服し、鋳造アルミニウム合金の材料のばらつきをより正確に捉える可能性を構築するものである。
8. 参考文献:
- Bao, Y., Wierzbicki, T., 2004. On fracture locus in the equivalent strain and stress triaxiality space. s.l.:International Journal of Mechanical Sciences.
- Engelen, R., 2005. Plasitcity induced Damage in Metals: nonlocal modelling at finite strains. s.l.:Habilitation thesis.
- Fagerholt, E.; et al., 2010. Experimental and numerical investigation of fracture in a cast aluminium alloy. s.l.:International Journal of Solids and Structures.
- Gurson, A. L., 1978. Porous rigid-plastic materials containing rigid inclusions-yield function, plastic potential and void nucleation. s.l.:The Physical Metallurgy of Fracture.
- Johnson, G. R., Cook, W. H., 1985. Fracture characteristics of three metals subjected to various strains, strain rates, terperatures and pressures. s.l.:Engineering Fracture Mechanics.
- Muehlstaetter, C., 2015. Versagensmodellierung von Al-Gusswerkstoffen. s.l.: Master Thesis, Upper Austrian University of applied sciences.
- Muehlstaetter, C., Hartmann, M., 2016. Material modelling of cast Aluminium by application of the Wilkins Damage Model. s.l.:ECCOMAS Congress Proceedia.
- Schiefermayr, K., Weiß, P., 2014. Wahrscheinlichkeits-rechnung und Statistik. s.l.:Course book, Upper Austrian University of applied sciences.
- Tvergaard, V., Needleman, A., 1984. An analysis of ductile rupture in notched bars. s.l.:Journal of the Mechanics and Physics of Solids.
- Wilkins, M. L., Streit, R. D., Reaugh, J. E., 1980. Cumulative-strain-damage model of ductile fracture: Simulation and prediction of engineering fracture tests. s.l.:s.n.
専門家Q&A:よくある質問への回答
Q1: なぜ統計的検定としてコルモゴロフ–スミルノフ(KS)検定が選ばれたのですか?
A1: 論文によると、コルモゴロフ–スミルノフ検定は、利用可能なデータ数が少ない場合でも正確な結果を提供するため、この研究に適していると判断されました。鋳造部品から切り出せる試験片の数には限りがあるため、少数のサンプルからでも信頼性の高い統計的結論を導き出せるこの手法は、実用的な研究開発において非常に有効です。
Q2: 応力三軸度とは何ですか? なぜ損傷モデリングで重要なのでしょうか?
A2: 応力三軸度は、静水圧応力とフォン・ミーゼス相当応力の比で定義され、応力状態が引張寄りか、せん断寄りかを示す指標です。この値が損傷モデリングで重要なのは、材料の破壊メカニズムが応力三軸度に大きく依存するためです。例えば、高い三軸度(引張が優勢)では空孔の成長と合体が破壊の主因となり、低い三軸度(せん断が優勢)ではせん断帯の形成が主因となります。したがって、破壊ひずみを正確に予測するには、応力三軸度を考慮することが不可欠です。
Q3: この確率論的モデルは、あらゆる鋳造合金に適用可能ですか?
A3: 本研究は特定のダイカスト製アルミニウム合金を対象としていますが、提案されている「損傷挙動のばらつきを統計的に捉える」というコンセプト自体は、不均一な微細組織を持つ他の多くの鋳造合金にも広く適用可能であると考えられます。ただし、具体的な確率分布の形状やパラメータ(平均値、標準偏差)は合金の種類や製造プロセスによって異なるため、対象となる材料ごとに同様の実験的キャラクタリゼーションが必要となります。
Q4: この確率論的モデルは、実際のFEシミュレーションでどのように実装されるのですか?
A4: 論文では、このコンセプトはシミュレーションモデルの各積分点(計算点)に対して、応力三軸度に応じた破壊ひずみ曲線を供給する「乱数生成器の入力」として使用されることを意図していると述べられています。つまり、シミュレーションを開始する前に、各要素に統計分布に基づいた異なる破壊特性を割り当てることで、材料全体の不均一性を仮想的に再現します。これにより、単一の結果ではなく、破壊確率の分布といった、より現実的な予測アウトプットを得ることができます。
Q5: Figure 4(平板引張)とFigure 5(マークラインせん断)を比較すると、せん断試験の方がばらつきが小さいように見えますが、なぜですか?
A5: 論文では、応力三軸度が η > 0.33 の領域(引張が優勢)に比べて、マークラインせん断試験(η ≈ 0)ではばらつきが小さいことが観測されたと記されています。これは、破壊メカニズムの違いに起因する可能性があります。引張優勢の状態では、鋳巣などの微小欠陥の存在や分布が空孔の成長・合体に大きく影響し、破壊ひずみのばらつきを増大させます。一方、せん断優勢の状態では、破壊がより均一なすべり変形に支配されるため、初期欠陥の影響が相対的に小さくなり、結果としてばらつきが抑制されると考えられます。
結論:より高い品質と生産性への道を切り拓く
鋳造アルミニウム部品の性能予測における長年の課題は、その本質的な材料のばらつきでした。本研究で示された「鋳造合金 損傷モデリング」への確率論的アプローチは、このばらつきを無視するのではなく、統計的にモデル化することで、シミュレーションの信頼性を飛躍的に向上させる画期的なブレークスルーです。この手法により、設計者は製品の破壊確率を予測し、より軽量で信頼性の高い部品を開発することが可能になります。
CASTMANでは、こうした最先端の業界研究を応用し、お客様の生産性と品質の向上を支援することに尽力しています。本稿で議論された課題がお客様の事業目標と一致する場合、ぜひ当社のエンジニアリングチームにご連絡ください。これらの原理をお客様のコンポーネントにどのように実装できるか、共に探求してまいります。
著作権情報
このコンテンツは、Christian Mühlstätter氏による論文「A Stochastic Approach for Damage Modelling of Cast Alloys」に基づく要約および分析です。
Source: https://doi.org/10.5220/0006909904670471
この資料は情報提供のみを目的としています。無断での商業利用は禁じられています。 Copyright © 2025 CASTMAN. All rights reserved.