鋳造アルミニウムおよび鋳造銅回転子を持つ誘導電動機におけるバー間電流について

この紹介資料は、「KTH Electrical Engineering」によって発行された論文「鋳造アルミニウムおよび鋳造銅回転子を持つ誘導電動機におけるバー間電流について (On Inter-bar Currents in Induction Motors with Cast Aluminium and Cast Copper Rotors)」に基づいています。

1. 概要:

• タイトル: 鋳造アルミニウムおよび鋳造銅回転子を持つ誘導電動機におけるバー間電流について (On Inter-bar Currents in Induction Motors with Cast Aluminium and Cast Copper Rotors)
• 著者: ALEXANDER STENING
• 発行年: 2010
• 発行学術誌/学会: KTH Electrical Engineering (Licentiate Thesis)
• キーワード: Induction motors (誘導電動機), Inter-bar currents (バー間電流), Copper rotors (銅回転子), Aluminium rotors (アルミニウム回転子), Starting torque (始動トルク), Asynchronous torques (非同期トルク), Starting current (始動電流), Stray losses (漂遊負荷損).

2. 抄録:

本論文は、誘導電動機の始動性能および漂遊負荷損に対するバー間電流の影響に関する研究を提示する。本研究は、アルミニウムおよび銅鋳造回転子間の性能差に焦点を当てている。
直入れ始動時の固定子電流を予測する手法が開発された。これには、表皮効果、漏れ磁束経路の飽和、および追加の鉄損のモデル化が含まれる。結果は測定によって検証された。バー間電流を考慮した解析モデルが導出され、高調波回転子電流のバー間抵抗率への依存性が調査された。バー間電流は、電動機の始動性能および漂遊負荷損にかなりの影響を与える可能性があり、その量は一次起磁力の高調波成分に強く依存することが見出された。
バー間抵抗率の測定に基づいて、アルミニウムおよび銅鋳造回転子の始動性能がシミュレーションされた。結果は、等価な銅回転子よりもアルミニウム回転子のプルアウトトルク（最大トルク）が高いことを示している。これは、銅回転子における空間高調波による制動トルクよりも、アルミニウム回転子の基本波始動トルクの増加によるものである。結果は測定によって検証された。プルアウトトルクの差は、モデルから計算されたものよりもさらに大きいことが見出された。これにより、バー間電流が電動機の始動性能にかなりの影響を与えることが結論付けられる。
定格速度では、制動トルクは銅回転子よりもアルミニウム回転子の方が大きい。これは、回転子かごにおける高調波ジュール損失の増加として見られる。シミュレーションにより、これらの損失は研究対象の機械の出力電力の1%にも達する可能性があることが示された。

3. 序論:

誘導電動機は、その単純さと堅牢な設計により、最も一般的に使用される電気機械である。効率的な電動機を設計するには、特に効率向上と厳しい始動性能要件に対する要求が高まる中で、正確なモデルが必要となる。漂遊負荷損（標準計算を超える追加損失）の低減は極めて重要である。鋳造回転子（アルミニウムおよび増加傾向にある銅）において、積層鉄心を介して回転子バー間を流れるバー間電流は、特に中小容量の電動機において、これらの損失の重要な構成要素として特定されている[2]。固定子スロット高調波の影響を受けるこれらの電流は、始動トルクおよびプルアウトトルクにも悪影響を与える可能性がある[6]。

ダイカストアルミニウム回転子は、中小容量の電動機で一般的である。鋳造技術の進歩により、ダイカスト銅回転子の製造が可能となり、より高い導電率と潜在的な効率向上が提供される。しかし、測定によると、銅回転子のバー間抵抗率はアルミニウム回転子よりも大幅に低い（最大10倍）可能性があり[9]、これはバー間電流の流れを促進する。

回転子スキューは、固定子スロット高調波によって誘起される高周波電流を抑制し、バーが絶縁されていれば効率を向上させるためにしばしば採用される。しかし、バー間抵抗率が低い鋳造回転子では、スキューがバー間電流を促進し、その利点を潜在的に相殺する可能性がある。その大きさは、スキューとバー間抵抗率に強く依存する。

本論文は、始動性能および追加の回転子損失をシミュレーションするための解析モデルを開発し、それらをアルミニウムおよび銅鋳造回転子（具体的には Motor A: 11 kW, 4極, 36/44 スロット, Al; Motor B: 11 kW, 4極, 36/28 スロット, Al & Cu）での測定によって検証することにより、これらの影響を研究することを目的とする。

4. 研究の概要:

研究トピックの背景:

高効率誘導電動機の必要性は、正確な性能モデルの要求を駆動する。漂遊負荷損、特にダイカスト回転子（アルミニウムおよび増加傾向にある銅）におけるバー間電流によって引き起こされるものは、効率と始動性能に大きな影響を与える。鋳造プロセス固有の低いバー間抵抗率、特に銅の場合は、回転子スキューのような設計特徴と複雑に相互作用する。

先行研究の状況:

過去の研究では、バー間電流損失[5, 6]を含む漂遊負荷損の構成要素が特定されている[2]。バー間抵抗を測定する方法が開発された[6, 9, 11]。バー間電流[14]、回転子バーの表皮効果[19, 20]、および飽和効果[21, 23, 25]に関する解析モデルが存在するが、これらの現象を統合し、特に鋳造アルミニウムと銅を比較するには、さらなる調査が必要である。

研究の目的:

鋳造アルミニウムおよび鋳造銅回転子を備えた誘導電動機の始動性能（トルク、電流）および漂遊負荷損（追加の回転子損失）に対するバー間電流の影響を調査すること。これには、これらの効果をシミュレーションできる解析モデルの開発と検証が含まれる。

核心研究:

本研究には以下が含まれる：

1. 開発されたテストリグと等価回路モデルを使用して、鋳造アルミニウムおよび銅回転子のバー間抵抗率を測定する。
2. 固定子および回転子の磁束鎖交、起磁力高調波、および回転子スキューを考慮して、バー間電流の分布と回転子バー電流への影響を計算するために、[14]に基づいた解析モデルを開発する。
3. 直入れ始動中の表皮効果（1D数値モデル[22]を使用）、漏れ経路飽和（解析/FEM組み合わせアプローチを使用）、および追加の鉄損を考慮に入れるための手法を開発する。
4. 異なるバー間抵抗率（絶縁、鋳造Al、鋳造Cuを表す）を持つ電動機について、始動トルク-速度特性および定格速度回転子損失をシミュレーションする。
5. 交換可能なアルミニウムおよび銅回転子を備えたテスト電動機（Motor B）での始動トルクおよび電流のFEMシミュレーションおよび実験測定を通じてモデルを検証する。
6. バー間電流の役割に焦点を当てて、アルミニウムと銅回転子間の性能差を分析する。

5. 研究方法論

研究設計:

本研究は、解析モデリング、数値シミュレーション、有限要素法（FEM）検証、および実験的検証を組み合わせて採用した。バー間電流の影響下で、鋳造アルミニウムと鋳造銅回転子（Motor B）間の性能差を分析する比較アプローチが用いられた。追加の電動機構成（Motor A）がパラメトリック解析研究に使用された。

データ収集および分析方法:

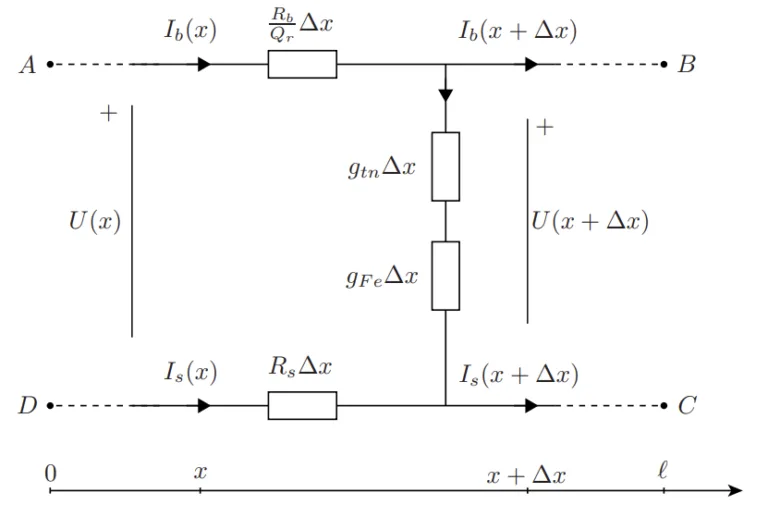
• バー間抵抗測定: 専用のテストリグが構築された（図 2.1, 2.2）。直流電流が印加され、電圧（UAB, UAD, UBC, UAX）が測定された。バー、シャフト、およびバー間抵抗/コンダクタンスを考慮した[9]に基づく等価回路モデル（図 2.3）を使用して、測定された電圧からバー間抵抗率（Rtn）を計算した（式 2.1-2.6）。
• 解析モデリング:
  • バー間電流: バーインピーダンス（Zbn）、バー間抵抗率（Rtn）、および鎖交磁束（Φsn, Φrn）を考慮した微分方程式（式 3.8, 3.43, 3.48）を境界条件（式 3.51）で解くことにより、[14]に基づいてモデルを導出した。
  • 磁束計算: 単純化された起磁力/パーミアンス分布（モデルA/B、図 3.4, 3.5, 3.9）のフーリエ解析を使用して空隙磁束密度を導出し、FEMで検証した（図 3.6）。回路要素によって鎖交される固定子および回転子磁束を計算した（式 3.26, 3.39, 3.42）。
  • 表皮効果: 1D数値法[22]を使用して、回転子バーの周波数依存インピーダンス補正係数（kr, kx）を計算した（図 4.1, 4.2, 4.3）。FEMで検証した（図 4.4-4.7）。
  • 飽和: 解析/FEM組み合わせアプローチを使用した。FEM固定子ロックテスト（図 4.10）および円線図解析（図 4.11）に基づいて、すべりによって変化する飽和係数（ksat、式 4.14）を定義し、漏れリアクタンスを修正した（式 4.13）。
  • 鉄損: 経験的係数（kLR, kLX）[22]に基づいて、等価回路内の追加の抵抗/リアクタンス成分としてモデル化した（図 4.13、式 4.20, 4.21）。
• シミュレーション: モデルを実装し（図 5.1）、異なるバー間抵抗率について速度範囲全体にわたるトルク成分（式 4.28, 4.29）および損失（式 4.22-4.25）を計算した。
• 実験的検証: フライホイールで負荷をかけたMotor B（AlおよびCu回転子を使用）で直入れ始動テストを実施した（図 5.5）。トルク（Magtrol TM-312）と速度を動的に測定した。データをフィルタリングし（図 5.6）、実効電流値を計算した。測定されたトルクと電流をシミュレーションと比較した（図 5.7, 5.9）。

研究トピックと範囲:

本研究は、鋳造回転子における有限のバー間抵抗率から生じるバー間電流が、以下に与える影響を定量化することに焦点を当てた：

• 始動トルク-速度特性（プルアウトトルクおよび非同期高調波トルクを含む）。
• 始動電流。
• 定格速度での追加の回転子損失（漂遊負荷損）。
  範囲には、始動中に関連する表皮効果、漏れ経路飽和、および関連する鉄損のモデル開発と統合が含まれた。本研究は主に、特定の4極、11kW電動機形状（Motor B、36/28スロット）について、スキュー付き鋳造アルミニウムおよび銅回転子を比較し、別の形状（Motor A、36/44スロット）に関する解析研究を含んだ。定格負荷時の高調波効果に対する主磁束飽和の影響は含まれていない。

6. 主要な結果:

主要な結果:

• 測定により、研究対象の形状において、鋳造銅回転子のバー間抵抗率は鋳造アルミニウム回転子と比較して大幅に低い（約10倍）ことが確認された。アルミニウム回転子ではバーに沿って不均一な抵抗率分布が示唆されたが、銅回転子ではより均一な分布が示された（第2章、表2.1、図2.7、図2.8）。
• 表皮効果計算のための数値手法が開発され、FEMシミュレーションに対して検証され、良好な相関を示したが、無視された歯先飽和のためにバー上部でわずかに過大評価された（第4章、図4.4-4.7）。
• 始動中の漏れ経路飽和を考慮に入れるために、解析計算とFEM結果を組み合わせた手法が開発され、飽和が始動電流を大幅に増加させる（約35%）ことが示された（第4章、図4.10、図4.12）。
• シミュレーションにより、バー間電流はスキューなし回転子の始動トルクには軽微な影響しか与えないが、スキュー付き回転子ではかなりの影響を与えることが示された。低いバー間抵抗率は、スロット高調波トルクを抑制するスキューの効果をなくし、プルアウトトルクを大幅に低下させる可能性がある（第3章、第4章、図3.17、図3.18、図4.15、図4.16）。
• テストされた電動機（Motor B、スキュー付き）について、シミュレーションは、バー間電流効果（Alの基本波トルク増加 vs Cuの高調波制動トルク）により、アルミニウム回転子が銅回転子よりも高いプルアウトトルク（4.5%）を持つと予測した（第5章、図5.2、図5.3）。
• 測定により、アルミニウム回転子のより高いプルアウトトルクが検証され、その差はシミュレーションされたものよりもさらに大きく（7%）、バー間電流が始動性能にかなりの影響を与えることを確認した（第5章、図5.8、図5.9）。
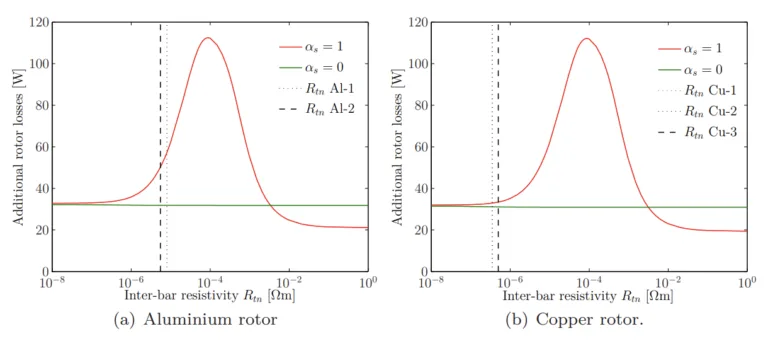
• シミュレーションにより、定格速度では、バー間電流による高調波ジュール損失（漂遊負荷損）は、銅回転子よりもアルミニウム回転子の方が大きく（より高いRtnのため）、研究対象の機械の出力電力の1%にも達する可能性があることが示された（第5章、図5.4）。

Figure 1.1: Stray-load loss components (0,2-37 kW induction motors) [2].

Figure 2.2: Conducting washer between test-plate and rotor short-circuit ring.

Figure 2.6: Two of the studied aluminium and copper rotors.

Figure 2.3: Equivalent circuit of the rotor used for the calculation of the inter-bar resistivity.

Figure 2.4: Calculated voltages for the aluminium rotor at a total current of 200 A. Figure 2.5: Calculated voltages for the copper rotor at a total current of 200 A.

Figure 4.2: The v th section of the rotor slot.

Figure 5.4: High frequency cage losses as a function of inter-bar resistivity Rtn at 75 ℃.

Figure 5.6: Measured and filtered torque and speed as a function of time.

Figure 5.5: Setup for measurements of starting torque.

図のリスト:

• 図 1.1 漂遊負荷損の構成要素（0.2-37 kW 誘導電動機）[2]。
• 図 2.1 バー間抵抗測定のための回転子テストセットアップ。
• 図 2.2 テストプレートと回転子短絡リング間の導電性ワッシャー。
• 図 2.3 バー間抵抗率計算に使用される回転子の等価回路。
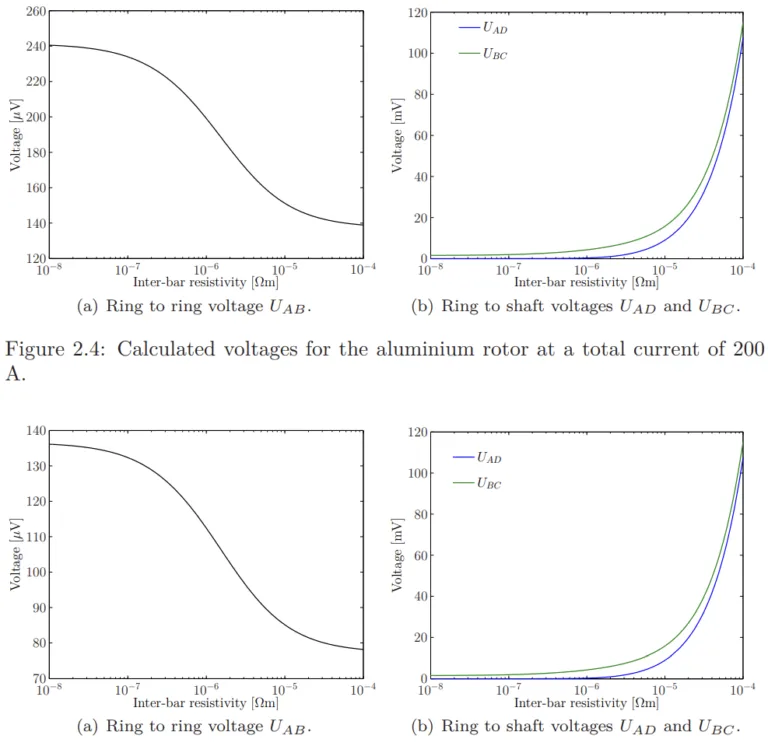
• 図 2.4 総電流200 Aにおけるアルミニウム回転子の計算電圧。
• 図 2.5 総電流200 Aにおける銅回転子の計算電圧。
• 図 2.6 研究対象のアルミニウムおよび銅回転子2つ。
• 図 2.7 総電流200 Aにおける回転子Al 2の測定および計算電圧UAX。
• 図 2.8 総電流100 Aにおける回転子Cu 2の測定および計算電圧UAX。
• 図 3.1 回転子回路の微小要素におけるバー電流とバー間電流の定義。
• 図 3.2 バー間電流間の位相変位。
• 図 3.3 バー間抵抗の定義。
• 図 3.4 位相aの電流による空隙磁束密度、モデルA。
• 図 3.5 位相aの電流による空隙磁束密度、モデルB。
• 図 3.6 無負荷時の解析的およびFEMシミュレーションによる空隙磁束密度の比較。
• 図 3.7 時刻t=0における回転子基準座標系でのn次波の位置。
• 図 3.8 バー番号kの電流と対応する空隙内の起磁力。
• 図 3.9 モデルAによって定義される空隙円周に沿ったパーミアンス変動。
• 図 3.10 境界x = -l/2における回転子電流。
• 図 3.11 バー間電流との相互作用による回転子バー電流の変化。
• 図 3.12 スキューなし回転子Aの基本波固定子ロック時バー間電流密度の大きさと結果の角度β1。
• 図 3.13 スキューなし回転子Aの基本波固定子ロック時バー電流の大きさと対応する角度γ1。
• 図 3.14 Rtn = 5・10^-5 Ωmのときの基本波および最初のスロット空間高調波ペアによってスキューなし回転子に生じる電流の大きさ。
• 図 3.15 スキュー付き回転子Aの基本波固定子ロック時バー間電流密度の大きさと結果の角度β1。
• 図 3.16 スキュー付き回転子Aの基本波固定子ロック時バー電流の大きさと対応する角度γ1。
• 図 3.17 Rtn = 5・10^-2 Ωmのときの基本波および最初のスロット空間高調波ペアによって1固定子スロットピッチ分スキューされた回転子に生じる電流の大きさ。
• 図 3.18 Rtn = 5・10^-5 Ωmのときの基本波および最初のスロット空間高調波ペアによって1固定子スロットピッチ分スキューされた回転子に生じる電流の大きさ。
• 図 4.1 様々なタイプの回転子バー。
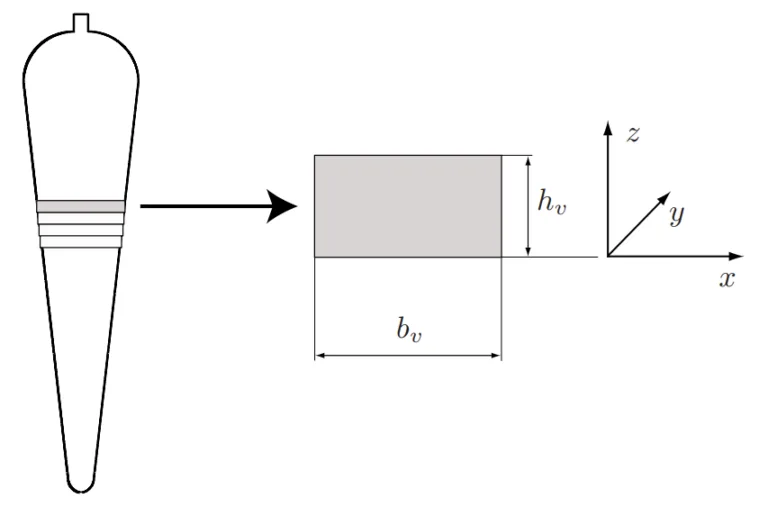
• 図 4.2 回転子スロットのv番目のセクション。
• 図 4.3 表皮効果を考慮するインピーダンス補正係数krおよびkxの計算手順。
• 図 4.4 アルミニウム回転子の固定子ロック時バー電流密度。
• 図 4.5 アルミニウム回転子のバー底部に対する固定子ロック時バー電流位相角。
• 図 4.6 銅回転子の固定子ロック時バー電流密度。
• 図 4.7 銅回転子のバー底部に対する固定子ロック時バー電流位相角。
• 図 4.8 研究対象の回転子スロットの表皮効果補正係数。
• 図 4.9 オンライン始動時の等価回路。
• 図 4.10 FEMシミュレーションによる固定子ロックテスト。
• 図 4.11 始動電流と最大トルク時の電流を定義する誘導電動機の簡略化された円線図。
• 図 4.12 回転子速度の関数としての飽和係数。
• 図 4.13 鉄損を考慮した追加抵抗。
• 図 4.14 スキューなし回転子Aの始動トルク。
• 図 4.15 1固定子スロットピッチ分スキューされた回転子Aの始動トルク。
• 図 4.16 1固定子スロットピッチ分スキューされた回転子Aの主要トルク成分。
• 図 5.1 異なる速度およびバー間抵抗率における電動機性能の計算手順。
• 図 5.2 1固定子スロットピッチ分スキューされた研究対象のアルミニウムおよび銅回転子のシミュレーション始動トルク。
• 図 5.3 測定されたバー間抵抗率の値で計算された研究対象のアルミニウムおよび銅回転子の始動トルク成分。
• 図 5.4 75℃におけるバー間抵抗率Rtnの関数としての高周波かご損失。
• 図 5.5 始動トルク測定のためのセットアップ。
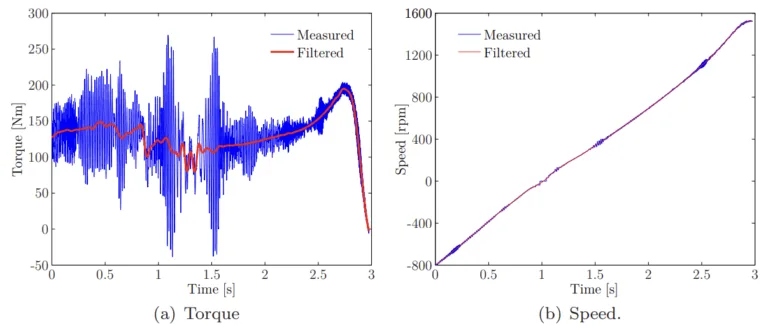
• 図 5.6 時間の関数としての測定およびフィルタリングされたトルクと速度。
• 図 5.7 シミュレーションおよび測定された始動電流。
• 図 5.8 定格電圧での直入れ始動時のアルミニウムおよび銅回転子の測定トルク。
• 図 5.9 定格電圧での直入れ始動時のアルミニウムおよび銅回転子のシミュレーションおよび測定トルク。

7. 結論:

表皮効果計算のための数値モデルがFEMで検証された。飽和と追加の鉄損を考慮して基本波始動電流を計算するために、解析/FEM組み合わせモデルが開発された。FEMシミュレーションにより、飽和と表皮効果により始動電流が約35%増加することが示された。バー間抵抗率を測定するためのテストリグが構築され、鋳造アルミニウムが銅よりも約10倍高い抵抗率を持ち、アルミニウム回転子は不均一な分布を示すことが明らかになった。バー間電流に関する解析モデルが導出された。シミュレーションにより、スキュー付き機械では抵抗率の低下に伴ってバー間電流密度が急速に増加し、スキューの効果がなくなり、これは[18]の知見と一致することが示された。

スキュー付き回転子では、バー間電流は始動性能にかなりの影響を与える。基本波周波数のバー間電流は有用なトルクに寄与する。スロット高調波のバー間電流は大きな非同期トルクを引き起こし、プルアウトトルクを低下させ、場合によっては始動を妨げる可能性がある（Motor A）。これらの効果は固定子/回転子スロットの組み合わせに強く依存する。

Motor B（AlおよびCu回転子）のシミュレーションと測定された始動特性の間で良好な一致が示された。シミュレーションは、Al回転子が等価なCu回転子よりも4.5%高いプルアウトトルクを持つと予測し、これは制動トルク（Cu）よりも基本波トルクの増加（Al）に起因するとされた。測定はこの傾向を確認し、差はさらに大きく（7%）、バー間電流が始動性能にかなりの影響を与えることを結論付けた。定格速度では、制動トルクおよび関連する高調波ジュール損失は、Cu回転子よりもAl回転子の方が大きく、出力電力の1%に達する可能性がある。

8. 参考文献:

• [1] A.R. Hagen, A. Binder, M. Aoulkadi, T. Knopik, and K. Bradley. Comparison of measured and analytically calculated stray load losses in standard cage induction machines. 18th International Conference on Electrical Machines, pages 1–6, 2008.
• [2] H. Nishizawa, K. Itomi, S. Hibino, and F. Ishibashi. Study on reliable reduction of stray load losses in three-phase induction motor for mass production. IEEE Transactions on Energy Conversion, EC-2:489–495, 1987.
• [3] A. Boglietli, A. Cavagnino, M. Lazzari, and A. Pastorelli. Induction motor efficiency measurements in accordance to ieee 112-b, iec 34-2 and jec 37 international standards. IEEE International Electric Machines and Drives Conference, 3:1599–1605, 2003.
• [4] A.A. Jimoh, R.D. Findlay, and M. Poloujadoff. Stray losses in induction machines: Part i, definition, origin and measurement. IEEE Transactions on Power Apparatus and Systems, PAS-104:1500–1505, 1985.
• [5] Y.N. Feng, J. Apsley, S. Williamson, A.C. Smith, and D.M. Ionel. Reduced losses in die-cast machines with insulated rotors. IEEE International Electric Machines and Drives Conference, pages 57–64, 2009.
• [6] A. M. Odok. Stray-load losses and stray torques in induction machines. Power Apparatus and Systems, Transactions of the American Institute of Electrical Engineers, 77(3):43–53, 1958.
• [7] P. L. Alger. Induction Machines: Their Behavior and Uses. Taylor & Francis, 1995.
• [8] A. Harson, P.H. Mellor, and D. Howe. Design considerations for induction machines for electric vehicle drives. Seventh International Conference on Electrical Machines and Drives, pages 16–20, 1995.
• [9] K. Dabala. Modified method to determine rotor bar-iron resistance in three-phase copper casted squirrel-cage induction motors. Proceedings of ICEM, pages 231–234, 2006.
• [10] P. L. Alger. Induced high-frequency currents in squirrel-cage windings. Power Apparatus and Systems, Transactions of the American Institute of Electrical Engineers, 76(3):724 – 729, 1957.
• [11] K. Dabala. A new experimental-computational method to determine rotor bar-iron resistance. Proceedings of ICEM, 2:69–72, 1996.
• [12] O. Aglén. Calorimetric Measurements of Losses in Induction Motors. Licentiate thesis, Royal Institute of Technology, Stockholm, Sweden, 1995.
• [13] A.H. Bonnett and T. Albers. Squirrel-cage rotor options for ac induction motors. IEEE Transactions on Industry Applications, pages 1197–1209, 2001.
• [14] A. Behdashti and M. Poloujadoff. A new method for the study of inter-bar currents in polyphase squirrel-cage induction motors. IEEE Transactions on Power Apparatus and Systems, PAS-98(3):902–911, 1979.
• [15] B. Heller and V. Hamata. Harmonic Field Effects in Induction Machines. Elsevier Science Ltd, 1977.
• [16] M. Ivanes and M. Bourmault. Etudes des pertes supplementaires dans les moteurs asynchrones. Technical report, Cie Electro-Mecanique, October 1968.
• [17] A. Behdashti. Contribution a l’etude des pertes supplementaires des machines asynchrones dans une tres large zone de fonctionnement. PhD thesis, L’Institut national polytechnique de Grenoble, June 1975.
• [18] A.C. Smith, S. Williamson, and C.Y. Poh. Distribution of inter-bar currents in cage induction machines. Second International Conference on Power Electronics, Machines and Drives, 1:297–302, 2004.
• [19] P. L. Alger and J. H. Wray. Double and triple squirrel cages for polyphase induction motors. Power Apparatus and Systems, Transactions of the American Institute of Electrical Engineers, 72(2):637 – 645, 1953.
• [20] M. Liwschitz-Garik. Skin-effect bars of squirrel-cage rotors. Power Apparatus and Systems, Transactions of the American Institute of Electrical Engineers, 73(1):255 – 258, 1954.
• [21] S. Williamson and D. R. Gersh. Finite element calculation of double-cage rotor equivalent circuit parameters. IEEE Transactions on Energy Conversion, 11(1):41–48, 1996.
• [22] C. Sadarangani. Electrical machines - design and analysis of induction and permanent magnet motors. KTH Hogskoletryckeriet, 2000.
• [23] P. D. Agarwal and P. L. Alger. Saturation factors for leakage reactance of induction motors. Power Apparatus and Systems, Transactions of the American Institute of Electrical Engineers, 79(3):1037–1042, 1960.
• [24] H. M. Norman. Induction motor locked saturation curves. Transactions of the American Institute of Electrical Engineers, 53(4):536 – 541, 1934.
• [25] B. J. Chalmers and R. Dodgson. Saturated leakage reactances of cage induction motors. Proceedings IEE, 116(8):1395–1404, 1969.
• [26] E. Alm. Elektroteknik, Band 3, Del 2B, Elektromaskinlära - Asynkronmaskinens teori, driftegenskaper och beräkning. Alb. Bonniers boktryckeri, 1931.
• [27] R. Chitroju. Improved Performance Characteristics of Induction Machines with Non-Skewed Asymmetrical Rotor Slots. Licentiate thesis, Royal Institute of Technology, Stockholm, Sweden, 2009.

9. 著作権:

• この資料は「ALEXANDER STENING」氏の論文です。「On Inter-bar Currents in Induction Motors with Cast Aluminium and Cast Copper Rotors」に基づいています。
• 論文の出典: [DOI URL placeholder - 利用可能な場合は実際のDOIを追加してください]

この資料は上記の論文に基づいて要約されており、商業目的での無断使用は禁じられています。
Copyright © 2025 CASTMAN. All rights reserved.