この紹介論文は、IJMERR が発行した「GATING DESIGN CRITERIA FOR SOUND CASTING」の研究内容です。
1. 概要:
- タイトル: GATING DESIGN CRITERIA FOR SOUND CASTING (健全な鋳造のためのゲート設計基準)
- 著者: Mazhar Iqbal
- 出版年: 2014
- 発行ジャーナル/学会: International Journal of Mechanical Engineering and Robotics Research (IJMERR)
- キーワード: ゲートシステム、スプルー、ランナー、インゲート、収縮
2. 抄録 / 序論
鋳造では、多孔性や不完全充填などの欠陥が発生する可能性があります。 ゲート/ライザーシステムの設計は、鋳造品質を向上させるために重要です。 この研究の目的は、不完全充填領域の削減、大きな多孔性の減少、歩留まりの向上など、鋳造品質を向上させるためにゲートシステムを最適化することです。
3. 研究背景:
研究テーマの背景:
ゲートシステムは、溶融金属を鋳型キャビティに供給するチャネルのネットワークです。 これには、湯だまり、スプルー、スプルーベースウェル、ランナー、ランナーエクステンション、インゲートなどの要素が含まれます (Rao PN, XXXX)。
既存の研究状況:
設計変数はしばしば相反するため、特定の鋳造、成形、および注入条件に基づいて妥協が必要です (Wallace J F and Evans E B, 1959; Sylvia J G, 1972)。
研究の必要性:
欠陥のない鋳造品を実現するには、さまざまな要件に対処するための体系的なアプローチが必要であり、適切なゲートシステム設計が不可欠です。
4. 研究目的と研究課題:
研究目的:
鋳造品質を向上させるためにゲートシステムを最適化すること。
主要な研究:
不完全充填の削減、多孔性の減少、歩留まりの向上。
5. 研究方法論
研究デザイン:
この方法論は、基本的な流体の流れの原理と確立された設計上の考慮事項のレビューに基づいています。
データ収集方法:
データ収集は、既存の文献と確立された鋳造慣行に依存しています。
分析方法:
分析では、ベルヌーイの定理や連続の法則など、確立された流体力学の原理を利用しています。
研究対象と範囲:
この研究は、さまざまな鋳造プロセスに適用可能なゲートシステム設計の原理に焦点を当てています。
6. 主要な研究結果:
主要な研究結果:
この論文は、ゲートシステム設計の原理と考慮事項に関する包括的な概要を提示します。
提示されたデータの分析:
- 流体の流れの原理: ベルヌーイの定理 (式 1)、連続の法則 (式 2)、およびレイノルズ数 (式 3) は、ゲートシステム内の流体の流れを説明するために提示されます。
- 設計変数: 迅速な金型充填、乱流の最小化、金型とコアの侵食の回避、スラグ/ドロス/介在物の除去、良好な温度勾配の促進、歩留まりの最大化、経済的なゲート除去、鋳造歪みの回避、既存の成形/注入方法との互換性を達成する方法について説明します。
- ゲートシステムの種類とレイアウト: 水平および垂直ゲートシステム、ならびに上部、パーティング、および下部ゲートが、それぞれの用途とともに説明されています。 インゲートの数と位置などのゲートチャネルレイアウトの考慮事項についても説明します。
- 鋳型充填現象: 流動性、金属静水圧、粘度、表面張力、熱拡散率、背圧、摩擦、および乱流。
- 最適充填時間: 充填時間の一般化された式が導入されています。
- ゲート要素の設計: スプルー、スプルーウェル、ランナー、およびインゲートの設計上の考慮事項が提示されます。 ゲート要素設計のフローチャートが提供されます (図 10)。
- 最適化と検証: 金型充填時間、インゲート速度、衝突、ゲート歩留まり、フェトリングなど、ゲート設計を評価するための基準について説明します。 作業現場試験、高速X線撮影、部分充填、オープンモールド研究、接触ワイヤセンシングなど、さまざまな検証技術が要約されています。
図表リスト:
- 図 1: ゲートシステムの要素 (Sylvia J G, 1972)
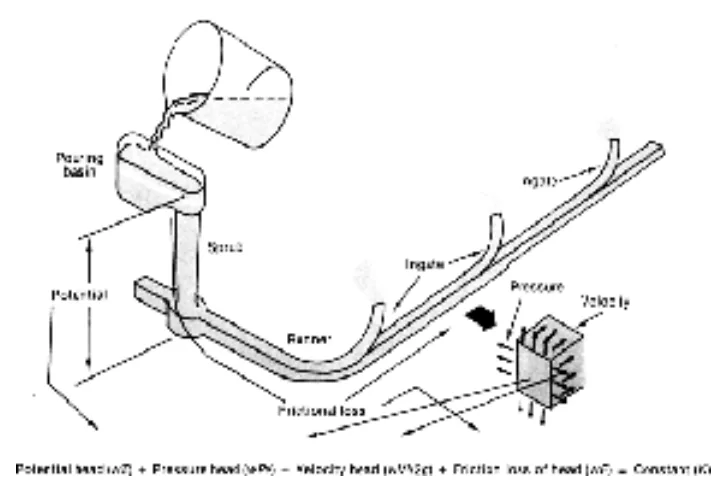
- 図 2: ベルヌーイの定理の図解 (Sylvia J G, 1972)
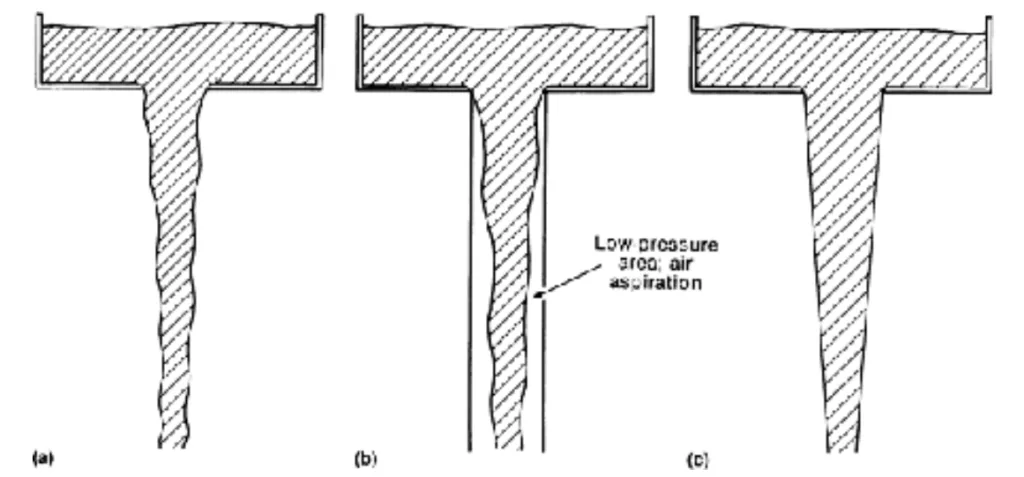
- 図 3: ストレートスプルーに対するテーパースプルーの利点を示す概略図。 (a) 自由落下する液体の自然な流れ。 (b) ストレートスプルー内の液体の流れによって誘発される空気吸引。 (c) テーパースプルー内の液体の流れ (Sylvia J G, 1972)
- 図 4: テーパースプルー内の液体の流れに近似するようにストレートスプルーに組み込まれたチョークメカニズム (a) チョークコア (b) ランナーチョーク (Sylvia J G, 1972)
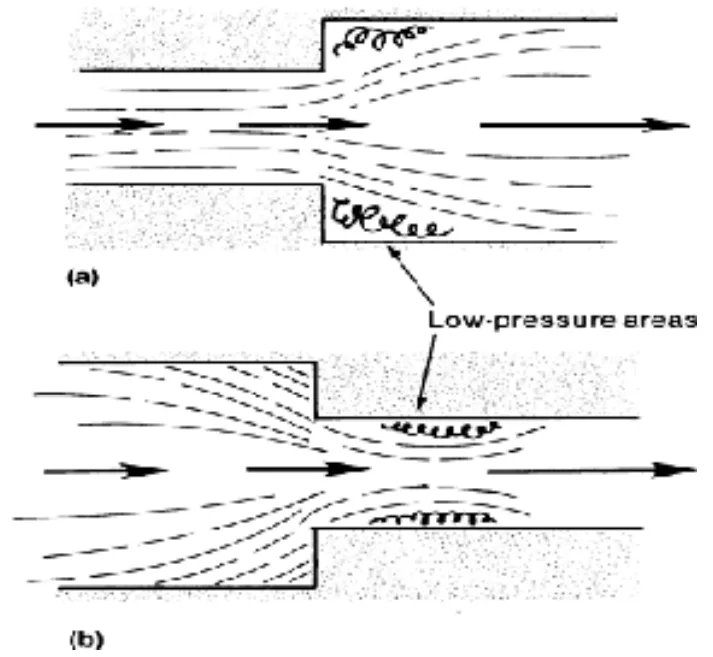
- 図 5: 流れチャネルの断面の急激な変化による低圧領域の形成を示す概略図 (a) チャネルの急激な拡大 (b) チャネルの急激な縮小
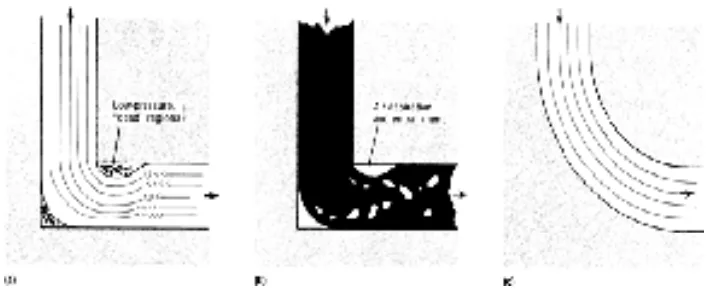
- 図 6: ゲートシステムにおける直角および曲線ベンド周辺の流体の流れを示す概略図 (a) 鋭い角による乱流 (b) 鋭い角による金属損傷 (c) 乱流と金属損傷を最小限に抑える流線型の角
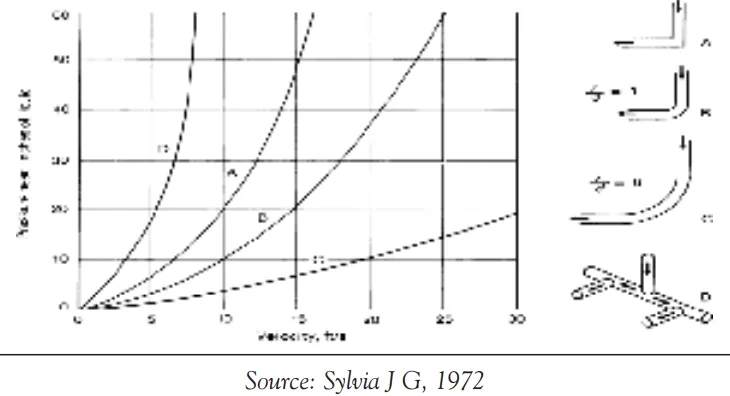
- 図 7: ゲート設計における圧力ヘッドと変化が金属の流れの速度に及ぼす影響: (a) 90° ベンド; (b) r/d = 1; (c) r/d = 6; (d) 複数の 90° ベンド。 変数 r と d は、それぞれランナーの曲率半径と直径です。
- 図 8: 充填されたシステムに対して 2 つのインゲートでのランナーからの流れにベルヌーイの定理を適用し、2 つのランナー構成に対するインゲートでの速度と圧力を比較する (a) 両方のインゲートで同じランナー断面 (b) 各インゲートで 2 つの異なるランナー断面を提供する階段状ランナー
- 図 9: インゲート位置のヒューリスティック
- 図 10: ゲート要素設計フローチャート
7. 結論:
主要な調査結果の要約:
- 湯だまり、スプルー、スプルーベースウェル、ランナー、およびランナーエクステンションは、清浄な溶融金属を鋳型キャビティに流入させるのに役立ちます。
- パーティングゲートが最も広く使用されているゲートです。
- 流体力学の法則と経験則が、最適なゲートシステムの設計に適用されます。
- 金属が鋳型キャビティに入る前に、ゲートシステムに入るスラグを完全に取り除くことが重要です。
- ライザーで供給されない孤立した部分の多孔性を低減するために、チルが必要になる場合があります。
研究の学術的意義:
さまざまな情報源からの知識を統合し、ゲートシステム設計の原則に関する包括的なレビューを提供します。
実用的な意味:
鋳造品質と歩留まりを向上させるためのゲートシステム設計に関する実用的なガイダンスを提供します。
研究の限界と今後の研究分野:
この研究は主に既存の文献に依存しており、新しい実験データは提示していません。 今後の研究では、実験的研究または計算モデリングを通じて、提示された原則を検証することに焦点を当てることができます。
8. 参考文献:
(英語版と同じ)
9. 著作権:
- この資料は「Mazhar Iqbal」の論文です: 「GATING DESIGN CRITERIA FOR SOUND CASTING」に基づいています。
- 論文ソース: www.ijmerr.com (論文ヘッダー、Vol. 2, No. 3, July 2014 より)
本資料は上記論文を紹介するために作成されたものであり、商業目的での無断使用を禁じます。
Copyright © 2025 CASTMAN. All rights reserved.