ダイカスト金型インサートにおける亀裂の発生と伝播の実験-数値モデル

本紹介内容は[ARCHIVES of FOUNDRY ENGINEERING]で発行された["Experimental-Numerical Model of the Initiation and Propagation of Cracks in Die Inserts"]の研究内容です。

Fig.1 a-d. Different stress states in a beam heated unilaterally

Fig.1 a-d. Different stress states in a beam heated unilaterally(continue)

1. 概要:

タイトル: Experimental-Numerical Model of the Initiation and Propagation of Cracks in Die Inserts (ダイインサートにおける亀裂の発生と伝播に関する実験的数値モデル)
著者: J. Piekło, M. Maj, St. Pysz
出版年: 2013年
出版ジャーナル/学会: ARCHIVES of FOUNDRY ENGINEERING, Volume 13, Special Issue 1/2013
キーワード: (論文に明示的なキーワードがないため、与えられた指示に従い、このセクションは省略する必要があります。)

2. 抄録 / はじめに

本論文で提示された研究の目的は、ダイインサートの寿命を予測するための実験的-数値的モデルを開発することであった。この目的のために、FEMを用いて、ダイカストマシンの安定した動作サイクル中のインサートの温度場と応力場を決定した。インサートが作られるWCL鋼に関する研究には、疲労試験と破壊力学の範囲の試験が含まれた。得られた結果から、ダイカストマシンの動作サイクル数とインサートの作業面に形成された亀裂の伝播速度との間の関係を導き出した。

3. 研究背景:

研究テーマの背景:

ダイカストプロセス用のダイに設置されたインサートは、金属射出、ダイ開口、保護コーティングスプレーの連続的に実行される操作によって引き起こされる、周期的に変化する熱的および機械的負荷の条件下で動作する。

既存の研究状況:

熱亀裂、応力誘起亀裂、およびスポーリングは分類できる。熱亀裂は平坦な表面に形成される。応力誘起亀裂は応力集中領域に現れる。スポーリングは、ダイ表面から剥離する脆性析出物の結果として形成される。

研究の必要性:

(これはダイインサートの寿命予測という文脈の中で暗黙的に言及されていますが、どの文章もこの点を直接的に扱っていません。ルールに従い、この点を総合することはできません。)

4. 研究目的と研究課題:

研究目的:

ダイインサートの寿命を予測するための実験的-数値的モデルの開発。

主要な研究:

ダイカストマシンの安定した動作サイクル中のインサートの温度場と応力場の決定。
疲労試験と破壊力学の範囲の試験。
ダイカストマシンの動作サイクル数とインサートの作業面に形成された亀裂の伝播速度との間の関係の導出。

5. 研究方法論

研究デザイン:

実験-数値モデリング。

データ収集方法:

エジェクター内部およびインサートとダイキャビティの間にドリルで開けられた穴に熱電対を配置。
AK 11合金に対して試験を実施。
パラメータには、射出温度(680°C)、サイクルタイム、型締力(150T)、金属圧力(70MPa)が含まれる。

分析方法:

有限要素法(FEM)を用いて温度場と応力場を決定。
2つの数値モデルを使用: 温度モデルと応力モデル。
縮小積分を用いた非線形要素を使用。
Morrow疲労寿命方程式とParis方程式を使用。

研究対象と範囲:

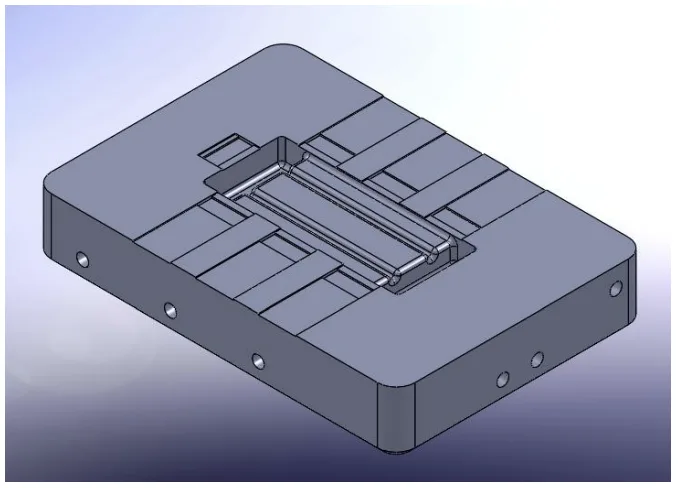
WCL鋼ダイインサート。
ダイカストマシンの安定した動作サイクル。

6. 主要な研究結果:

主要な研究結果:

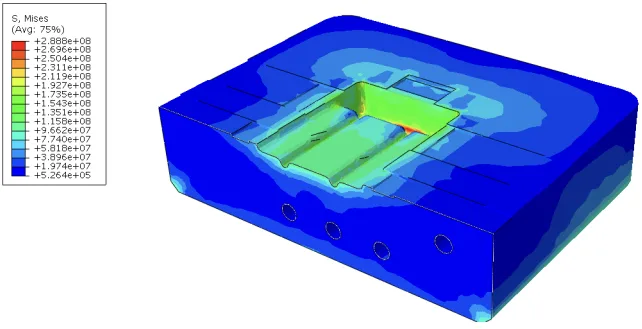
応力と温度の分析に基づいて、インサートを3つのゾーン(A、B、C)に区分。
Aゾーン(表面から5mmの深さ)は、最大の温度変化(260°C〜670°C)と熱応力の符号変化を経験。熱疲労がこのゾーンの破壊の主な原因。
Bゾーン(5mmから25mmの深さ)は、高く変化する値を持つ圧縮応力を有する。周期的クリープが金属強度に影響を与えると仮定。
Cゾーン(25mmより深い)は、200MPaを超えない圧縮応力を有する。単調クリープが高温強度を制御すると仮定。
Morrow方程式(実験的に決定された定数を含む)を用いて、亀裂開始までのサイクル数を予測(約60,000サイクル)。
亀裂伝播速度はParis方程式から予測され、定数m = 2.88およびC = 7.9 * 10-12が実験的に決定された。
瞬間亀裂長さに従う関数としてΔKが表現されたParis方程式: da/dN = 1.25 * 10^(-4) * a。

提示されたデータの分析:

Table 1: さまざまな亀裂長さについて、数値的に計算されたサイクルと実験的に測定されたサイクルの比較を示す。計算値と測定値の差は「それほど大きくない」と述べられている。

Fig. 3 Recorded experimentally (curve 1) and calculated
numerically (curve 2) temperature changes in the die insert during
one operating cycle of the die casting machine — Fig. 3 Recorded experimentally (curve 1) and calculated numerically (curve 2) temperature changes in the die insert during one operating cycle of the die casting machine

Fig. 4. Calculated by FEM changes in stress components and
in reduced stress in the die insert during one operating cycle of the
die casting machine — Fig. 4. Calculated by FEM changes in stress components and in reduced stress in the die insert during one operating cycle of the die casting machine

Fig. 5. Field of reduced instantaneous thermal stresses induced by temperature field

図のリスト:

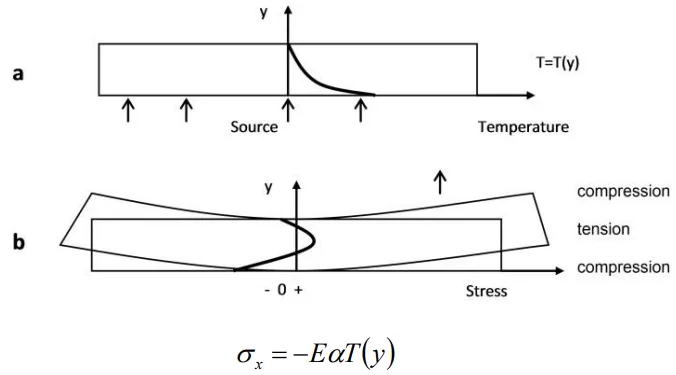
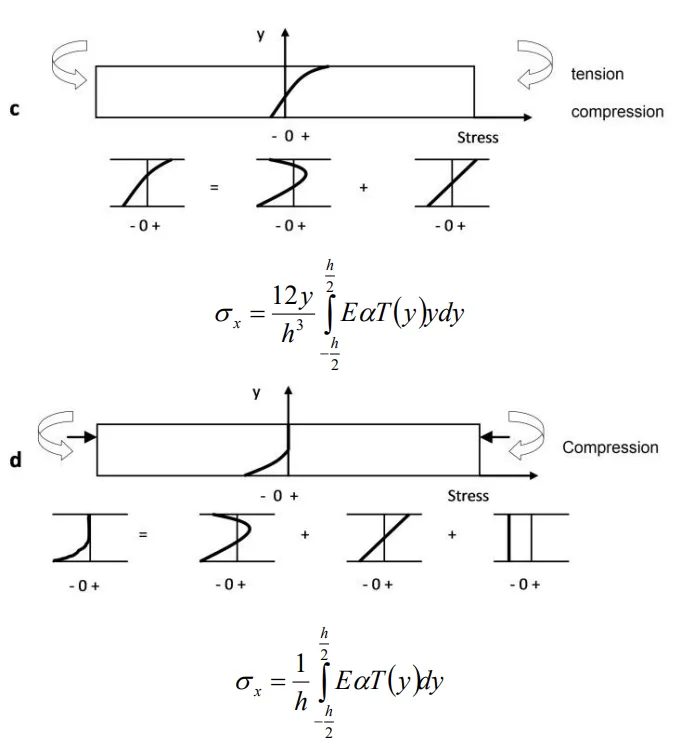
Fig.1 a-d. 片側から加熱された梁のさまざまな応力状態
Fig. 2 ダイインサートのCADモデル
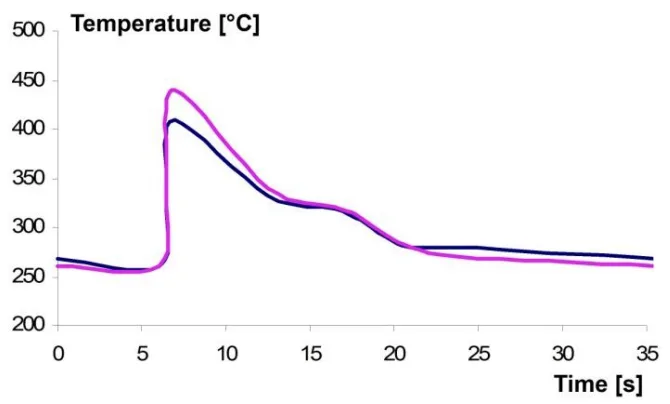
Fig. 3 ダイカストマシンの1回の動作サイクル中のダイインサートにおける実験的に記録された(曲線1)および数値的に計算された(曲線2)温度変化
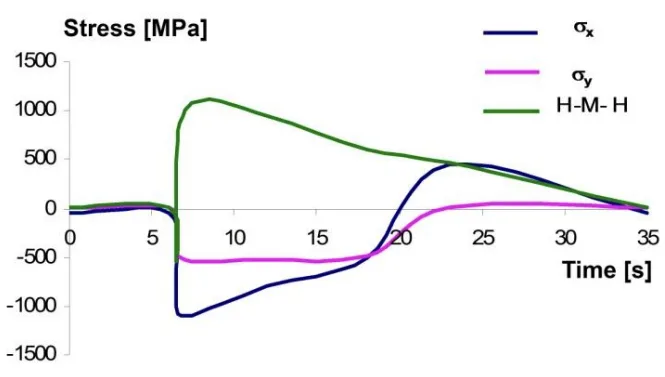
Fig. 4. ダイカストマシンの1回の動作サイクル中のダイインサートにおける応力成分および低減応力のFEM計算による変化
Fig. 5. 温度場によって誘発された低減された瞬間熱応力場

7. 結論:

主要な結果の要約:

周期的応力変化は主に表面で発生し、5mmの深さまで浸透。
圧縮応力が支配的であるが、冷却中の引張応力が亀裂伝播を制御。
計算モデルは、亀裂の位置と成長率を予測可能。

研究の学術的意義:

ダイカストインサートにおける亀裂の発生と伝播を分析するための、結合された実験的数値モデルを提供する。

実用的な意味:

ダイインサートの寿命予測を可能にする。
採用された計算モデルは、亀裂が発生する可能性が最も高い場所を決定することを可能にし、考慮された実際のインサートの摩耗度に関する収集されたデータを参照して、合理的な精度で成長率を計算することも可能にする。

研究の限界と今後の研究分野:

実験結果は1つの標本に対する測定値。

8. 参考文献:

[1] Suzuki, M., Ishihara, M. & Miyachi, H. (1974). Innere Spannung und Bradrissbildung In Druckgiessformen. Giesserei - Praxis. 4, 63-70.
[2] Danzer, R., Strum, F., Schindler, A. & Zlepping, W. (1983). Temperaturwechselrisse in Druckgiessformen. Giesserei Praxis. 19, 287-297.
[3] Rosbrook, C., Shivpuri, R. (1993). A Computer Aided Investigation of Heat Checking and Die Life Predictions in Die Casting Dies, Materiały z konferencji w Cleveland.
[4] Kocańda, S., Szala, J. (1985). Podstawy obliczeń zmęczeniowych. Warszawa: PWN.
[5] German, J., Biel-Gołaska, M. (2004). Podstawy i zastosowanie mechaniki pękania W zagadnieniach inżynierskich. Kraków: Instytut Odlewnictwa.
[6] Neimitz, A. (1998). Mechanika pękania. PWN.
[7] Statute study 11.11.170.318 Task 10/11

9. 著作権:

本資料は"J. Piekło, M. Maj, St. Pysz"の論文: "Experimental-Numerical Model of the Initiation and Propagation of Cracks in Die Inserts"に基づいています。
論文出典: (提供されたOCRにDOI URLがないため、省略する必要があります。)

PDF View

Tags: CAD; ,Die casting; ,temperature field; ,金型; ,금형