この技術概要は、Lin-Lin Chen、Shuo-Yan Chou、Tony C Wooによる学術論文「Parting directions for mould and die design」(Computer-Aided Design、1993年)に基づいています。HPDC(ハイプレッシャーダイカスト)の専門家のために、CASTMANのエキスパートが要約・分析しました。
キーワード
- プライマリーキーワード: パーティング方向の最適化
- セカンダリーキーワード: 金型設計、計算幾何学、アンダーカットとコア、可視性マップ、離型性、射出成形
エグゼクティブサマリー
- 課題: 金型設計において、パーティング方向の選定は、必要なコアの数を決定する重要なステップであり、工具コスト、金型の複雑さ、サイクルタイムに直接影響します。
- 手法: 研究者たちは、計算幾何学を用いて最適なパーティング方向を見つけるための決定論的アルゴリズムを開発しました。この手法では、対象物を「ポケット」に分解し、各ポケットの離型性を球体上の「可視性マップ」として表現します。
- 主要なブレークスルー: この研究は、複雑な設計問題を解決可能な幾何学的課題に変換しました。つまり、球体上でこれらの可視性マップの最大数と交差する一対の対向する点を見つけることで、コアの必要性を最小限に抑えることができます。
- 結論: このアルゴリズム的アプローチは、パーティング方向を選定するための保証された最適な解決策を提供し、従来のヒューリスティクスや推測を超えて、工具コストを削減し、成形プロセス全体を簡素化します。
課題:なぜこの研究がHPDC専門家にとって重要なのか
何十年もの間、エンジニアはパーティング方向とパーティング面の選定が金型設計の基本的なステップであることを理解してきました。この選択が、アンダーカット(製品の金型からの取り外しを妨げる凹みや突起)を処理するために必要なコアの数と形状を決定します。コアを使用すると、工具コストが増加し、金型の操作が複雑になり、生産サイクルが遅くなる可能性があります。業界の一般的なルールは、コアの数を最小限に抑えるパーティング方向を選択することです。
しかし、この重要なステップの自動化は、これまでほとんど注目されてきませんでした。従来のアプローチは、パーティング方向を三つの主軸の一つに合わせるか、ランダムに生成された方向のセットから選択するなど、しばしば限定的でした。これらの手法の欠点は、真に最適なパーティング方向が果たして存在するのか、あるいは一つが他より優れているのかを知ることが不可能である点です。この論文は、最適なパーティング方向のペアを見つけるための決定論的な手法を開発することにより、まさにその問題に取り組んでいます。
アプローチ:手法の解明
この課題を解決するために、研究者たちは計算幾何学に基づいた新しいアプローチを開発しました。この手法の中核は、「離型性」の条件を正確に定義することです。
あるサーフェスが特定の方向に沿って離型可能であるとは、それが妨げられることなく金型から取り外せる場合を指します。この条件は、サーフェス全体がパーティング方向に沿って「完全に可視」である場合に満たされます。可視でないサーフェスやその一部はアンダーカットとなり、コアが必要になります。
この研究の方法論は次のように分類できます:
- オブジェクトの分解: 対象物は計算論的に「ポケット」の集合に分解されます。各ポケットの可視性と離型性は、その後独立して決定できます。
- 可視性マップ(VMaps): 各ポケットに対して「可視性マップ」が構築されます。このVMapは単位球の表面上の凸領域であり、そのポケットが完全に可視であり、したがって離型可能であるすべての可能な方向を表します。
- 球状ポリゴンの被覆: 問題は次に変換されます。最適な一対の対向するパーティング方向を見つけることは、VMapの最大数に含まれる球体上の一対の対極点を見つける問題となります。この点のペアでカバーされないVMapに対応するサーフェスは、コアを必要とします。
この手法は、すべての可能なパーティング方向を体系的かつ網羅的に分析し、数学的に最適な解決策を見つける方法を提供します。
ブレークスルー:主要な発見とデータ
この研究は、金型設計の重要な段階を最適化できる堅牢なアルゴリズムを生み出しました。その主要な発見は、新たなレベルの精度と効率を提供します。
- 発見1:解決可能な幾何学的問題: この研究は、パーティング方向の選定という、しばしば直感的で複雑なタスクを、「対極点による球状ポリゴン被覆」という明確に定義された計算問題に再構成することに成功しました。これにより、複雑な製造問題を幾何学的アルゴリズムで解決することが可能になります。
- 発見2:保証された最適解: 本論文は、最適なパーティング方向を決定するためのアルゴリズムを提示しています。「m」個のポケットと「n」個の頂点を持つオブジェクトに対して、アルゴリズムはO(nm log m)時間で実行されます。従来のヒューリスティックな手法とは異なり、このアプローチは必要なコアの数を最小化する解を見つけることを保証します。
- 発見3:重み付き最適化: このアルゴリズムは、各ポケットにその幾何学的複雑さや推定製造コストに基づいて「重み」を割り当てるように変更できます。これにより、最適化は単にコアの数を最小化するだけでなく、最も困難なコアのコストと複雑さを最小化することに焦点を当てることができます。
貴社のHPDC製品への実践的な示唆
本論文の結果と結論に厳密に基づくと、これらの発見は現代の製造環境に直接的かつ実践的な示唆を与えます。
- プロセスエンジニア向け: 「アルゴリズム」セクションの知見は、金型設計に計算論的アプローチを採用することで、絶対的に最良のパーティング方向を体系的に特定できることを示唆しています。これにより、従来の経験に基づく設計ルールで含まれていたかもしれないコアを削減または排除し、プロセスを簡素化し、潜在的な故障点を減らすことができます。
- 品質管理向け: 最適なパーティング方向と最小限のコア数との相関関係は、より堅牢なプロセスへの道筋を示します。可動部品(コア)が少ないシンプルな金型は、本質的に操作と保守が容易であり、部品ごと一貫性の向上やプロセス偏差の早期発見につながる可能性があります。
- 金型設計向け: このパーティング方向の最適化に関する研究は、現代のCAD/CAMソフトウェアが、設計者を最初から数学的に最適な解決策に導くアルゴリズムで強化できることを示唆しています。論文の結論で詳述されているように、このデータ駆動型アプローチは、コストのかかる設計の繰り返しを減らし、複雑な形状の部品に取り組むための強力なツールを提供します。
論文詳細
Parting directions for mould and die design
1. 概要:
- タイトル: Parting directions for mould and die design (金型設計のためのパーティング方向)
- 著者: Lin-Lin Chen, Shuo-Yan Chou, and Tony C Woo
- 出版年: 1993年
- 掲載誌/学会: Computer-Aided Design, Volume 25, Number 12
- キーワード: manufacturing, algorithms, computational geometry, injection moulding, die casting, parting directions, visibility (製造、アルゴリズム、計算幾何学、射出成形、ダイカスト、パーティング方向、可視性)
2. 抄録:
離型性の条件に基づき、完全可視性と部分可視性という2つのレベルの可視性が定義される。サーフェスが完全に可視である視野方向は、単位球上の凸領域として表現でき、これをサーフェスの可視性マップと呼ぶ。与えられたオブジェクトをポケットに分割し、各ポケットの可視性と離型性を独立して決定し、可視性マップを構築し、コアの数を最小化する最適なパーティング方向のペアを選択するためのアルゴリズムが示される。一例がアルゴリズムを説明する。
3. 序論:
ダイカストおよび射出成形において、基本的な金型は、一対の反対のパーティング方向に沿って分離する2つのプレートで構成される。製品の取り外しを妨げる製品上の突起や凹部はアンダーカットと呼ばれ、コアやインサートのような製造装置を必要とする。パーティング方向の選択は、これらのコアの数と形状を決定するため、極めて重要である。コアは工具コストとプロセスの複雑さを増大させるため、主な目標は必要なコアの数を最小化するパーティング方向を選択することである。このステップを自動化する過去の試みは限定的であり、最適な解決策を保証できなかった。
4. 研究の要約:
- 研究トピックの背景: この研究は、金型設計において、製品が金型から取り外せること(離型性)を保証しつつ、製造の複雑さとコストを最小化するパーティング方向を選択するという基本的なニーズに基づいている。
- 先行研究の状況: 先行研究は、パーティング方向を主軸に限定するか、ヒューリスティックな(例:ランダムに生成された)アプローチを使用していた。これらの手法には、より良い解決策が存在するかどうか、あるいは実行可能な解決策が見つかったかどうかを知る方法がなかった。
- 研究の目的: 本研究の目的は、与えられたオブジェクト形状に対して必要なコアの数を最小化する最適なパーティング方向のペアを見つけるための決定論的な手法を開発することであった。
- 研究の中核: 研究の中核は、離型性を「完全な可視性」の観点から定義し、可視性を球体上の「VMap」として表現し、VMapの最大数でカバーされる対極点(パーティング方向)のペアを見つけるアルゴリズムを開発することにある。
5. 研究方法論
- 研究設計: この研究は計算幾何学の問題として設計された。「可視性」という幾何学的特性と「離型性」という製造特性との間に形式的な関係を確立した。問題はその後、「対極点による球状ポリゴン被覆」問題に変換され、そのためのアルゴリズムが開発された。
- データ収集と分析方法: この方法論は経験的なデータ収集を伴わず、アルゴリズム開発と幾何学的分析に基づいている。オブジェクトのジオメトリ(多面体モデル)が入力として機能する。分析には、凸包の計算、「ポケット」の特定、各ポケットの「可視性マップ」の生成、そして最適な解を見つけるための結果として得られる球状分割の探索が含まれる。
- 研究トピックと範囲: 範囲は多面体オブジェクトに焦点を当てている。この研究は、オブジェクトをポケットに分割し、可視性マップを構築し、コアの数を最小化するために最適なパーティング方向のペアを選択するアルゴリズムを開発する。
6. 主要な結果:
- 主要な結果: 主な結果は、m個のポケットとn個の頂点を持つオブジェクトの最適なパーティング方向を決定できるO(nm log m)時間のアルゴリズムである。この研究はまた、アルゴリズムが重み付きポケットを扱うように変更でき、単にコアの数だけでなく、製造コストや複雑さに基づく最適化を可能にすると結論付けている。
- 図の名称リスト:
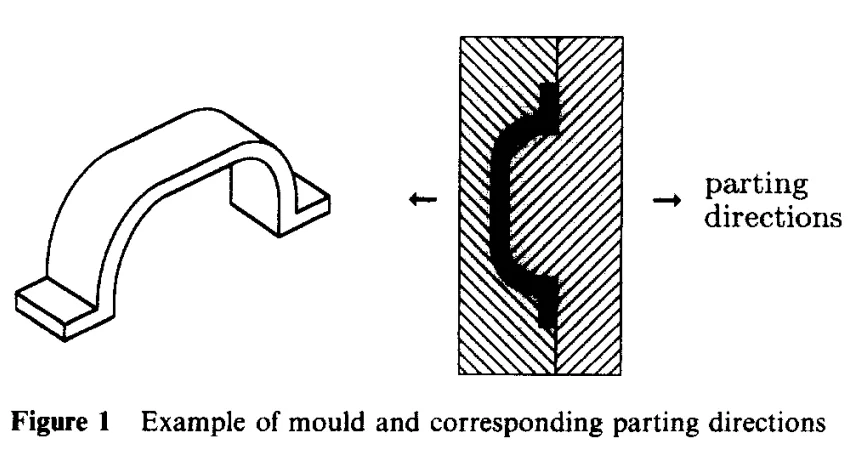
- Figure 1: 金型と対応するパーティング方向の例
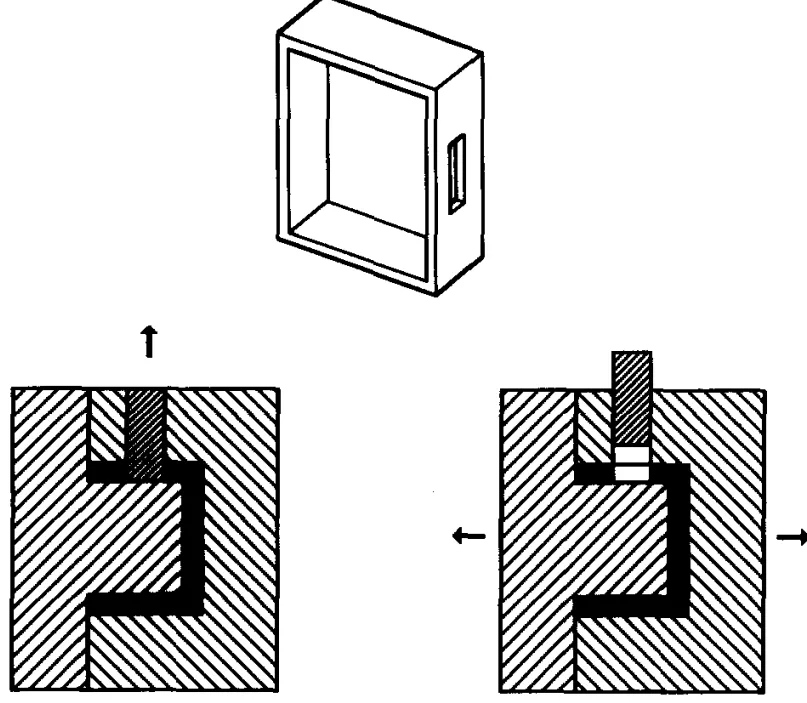
- Figure 2: 外部の凹みのためにサイドコアを必要とするオブジェクトの例
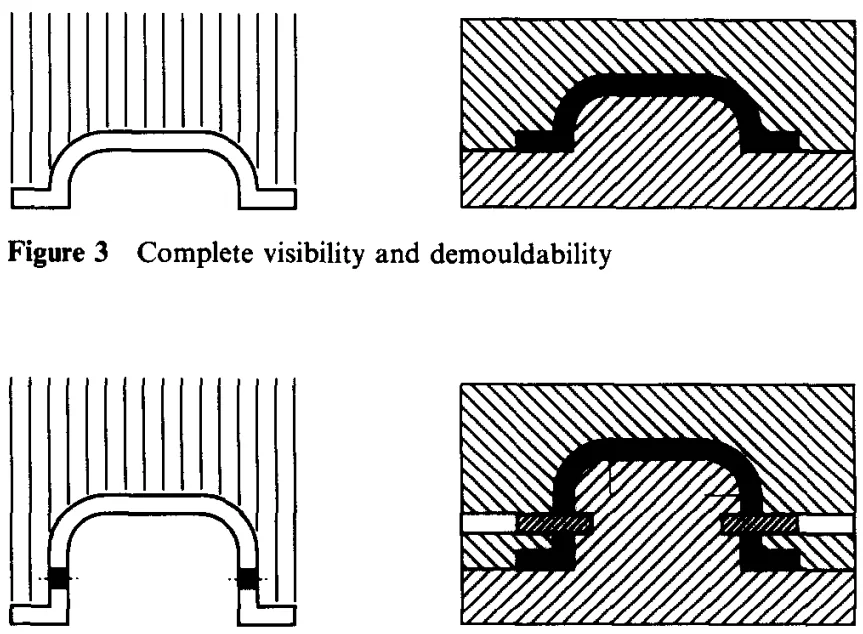
- Figure 3: 完全な可視性と離型性
- Figure 4: 部分的な可視性とコアの使用
- Figure 5: サーフェスとその対応するGMapとVMapの例
- Figure 6: オブジェクト;(a) オブジェクト、(b) その凸包、(c) 対応する密閉ポケット、(d) ポケット
- Figure 7: 対極点による球状ポリゴン被覆
- Figure 8: 2つの隣接セルとその所有権ベクトル
- Figure 9: Figure 6のオブジェクトのポケットとその対応するVMap
- Figure 10: Figure 9のVMapとその反対側によって誘起される球状分割
7. 結論:
すべてのコアが等しく望ましくないと仮定して、オブジェクトの最適なパーティング方向を決定するためのO(nm log m)時間のアルゴリズムが開発された。このアルゴリズムは、各ポケットにその幾何学的複雑さや製造コストに基づいて重みを割り当てるように変更でき、より微妙な最適化が可能である。著者らはまた、本論文では完全に見えないポケットにはコアが使用されると仮定しているが、将来の研究では「部分的な可視性」の概念を援用してポケットを細分化することを検討でき、それによって場合によってはコアを完全に排除できる可能性があると述べている。
8. 参考文献:
- Bralla, J G (Ed.) Handbook of Product Design for Manufacturing: A Practical Guide to Low-Cost Production McGraw-Hill (1986)
- Campbell, J Castings Butterworth-Heinemann (1991)
- Pye, R G W Injection Mold Design: A Textbook for the Novice and a Design Manual for the Thermoplastics Industry (4th Ed.) John Wiley (1989)
- Rubin, I I Handbook of Plastic Materials and Technology John Wiley (1990)
- Kalpakjian, S Manufacturing Processes for Engineering Materials Addison-Wesley (1991)
- Lee, K and Smith, C T 'Computer-aided pattern design for casting processes' Manufacturing Processes, Systems & Machines Proc. 14th Conf. Production Research & Technology (1987) pp 365-371
- Ravi, B and Srinivasan, M N 'Decision criteria for computer-aided parting surface design' Comput.-Aided Des. Vol 22 No 1 (1990) pp 11-18
- Smith, C T and Lee, K 'Computer-aided pattern design for casting processes' AFS Trans. (1986) pp 21-28
- Ganter, M A and Tuss, L L 'Computer-assisted parting line development for cast pattern production' AFS Trans. (1990) pp 795-800
- Hui, K C and Tan, S T 'Mould design with sweep operations - a heuristic search approach' Comput.-Aided Des. Vol 24 No 2 (1992) pp 81-91
- O'Rourke, J Art Gallery Theorems and Algorithms Oxford University Press (1987)
- Toussaint, G T 'Computing visibility properties of polygons' in Pattern Recognition and Artificial Intelligence North-Holland (1988)
- Stolfi, J Oriented Projective Geometry: A Framework for Geometric Computations Academic Press (1991)
- Struik, D J Lectures on Analytic and Projective Geometry Addison-Wesley (1953)
- Hilbert, D and Cohn-Vossen, S Geometry and the Imagination Chelsea (1952)
- Chen, L L and Woo, T C 'Computational geometry on the sphere for automated machining' ASME J. Mech. Des. Vol 114 No 2 (1992) pp 288-295
- Hoffmann, C M Geometric and Solid Modeling: An Introduction Morgan Kaufmann (1989)
- Edelsbrunner, H Algorithms in Combinatorial Geometry Springer-Verlag (1987)
- Preparata, F P and Hong, S J 'Convex hulls of finite sets of points in two and three dimensions' Commun. ACM Vol 2 No 20 (1977) pp 87-93
- Tang, K and Woo, T C 'Algorithmic aspects of alternating sums of volumes. Part 1: Data structure and difference operation' Comput.-Aided Des. Vol 23 No 5 (1991) pp 357-366
専門家Q&A:あなたのトップの質問に答えます
Q1: この研究で金型設計を改善するために特定された最も重要な単一の要因は何でしたか?
A1: この研究は、最適なパーティング方向のペアの選択が、必要なコアの数を最小化するための最も重要な要因であると結論付けました。これは「Introduction」で詳述され、論文で提示されたアルゴリズムによって解決されます。
Q2: この研究は、問題に対処するための従来の方法とどのように比較されますか?
A2: 論文のIntroductionでは、従来の方法が主軸への選択肢の制限やランダムに生成された方向の使用などのヒューリスティクスに依存しているのに対し、この研究はコアの数を最小化するパーティング方向を見つけることを保証する決定論的アルゴリズムを導入していると指摘しています。
Q3: この発見はすべての種類の合金に適用可能ですか、それとも特定の合金に限定されますか?
A3: Methodologyセクションで説明されているように、この研究は多面体オブジェクトのジオメトリに基づいて行われました。したがって、その適用可能性は特定の材料や合金ではなく、オブジェクトの形状に基づいています。
Q4: 研究者たちがこの結論に至るために使用した特定の測定またはシミュレーション技術は何ですか?
A4: 研究者たちは、「PARTING DIRECTIONS」セクションで説明されているように、ガウス球上に「可視性マップ」(VMaps)を作成し、その後「点による球状ポリゴン被覆」のためのアルゴリズムを開発するという計算幾何学を利用して、問題を定量化し解決しました。
Q5: 論文によると、主な限界または将来の研究分野は何ですか?
A5: 著者らはConclusionsで、将来の研究の主要な分野は、「部分的な可視性」の概念を援用してポケットの細分化を考慮するアルゴリズムを開発することであり、それによって、そうでなければ必要となるコアを場合によっては完全に排除できる可能性があると述べています。
Q6: この論文からダイカスト施設が得られる直接的で実践的な教訓は何ですか?
A6: 中核となる教訓は、体系的でアルゴリズム的なアプローチを用いてパーティング方向の選択を最適化することにより、数学的に保証された最小限のコア数を達成することが可能であり、それが工具コストの大幅な削減と金型操作の簡素化につながる可能性があるということです。これは、論文「Parting directions for mould and die design」の全体的な結果によって強く支持されている中心的な結論です。
結論と次のステップ
この研究は、ダイカストおよび金型設計を強化するための貴重なロードマップを提供します。ヒューリスティクスに基づく決定からデータ駆動型のアルゴリズム的アプローチに移行することにより、この発見は品質の向上、工具コストの削減、そして生産プロセス全体の最適化に向けた明確な道筋を示しています。
CASTMANでは、お客様の最も困難なダイカストの問題を解決するために、最新の業界研究を応用することに専念しています。この論文で議論されている課題が貴社の運用目標と共鳴するものであれば、これらの先進的な原則を貴社のコンポーネントにどのように実装できるか、当社のエンジニアリングチームにご相談ください。
著作権
- この資料は、"Lin-Lin Chen, Shuo-Yan Chou, and Tony C Woo"による論文です。"Parting directions for mould and die design"に基づいています。
- 論文の出典: Computer-Aided Design, Volume 25, Number 12, December 1993. 文書内に特定のDOI URLは提供されていません。
- この資料は情報提供のみを目的としています。無断での商業利用は禁じられています。
- Copyright © 2025 CASTMAN. All rights reserved.