CFDを用いた高圧ダイカストマシンのショットスリーブにおける臨界速度の決定について

本稿は、「Preprint submitted to Elsevier」により発行された論文「On determining the critical velocity in the high-pressure die casting machine's shot sleeve using CFD」に基づいています。

1. 概要:

• タイトル: On determining the critical velocity in the high-pressure die casting machine's shot sleeve using CFD
• 著者: S. Kohlstädt, M. Vynnycky, S. Goeke, A. Gebauer-Teichmann
• 発行年: 2019
• 発行学術誌/学会: Preprint submitted to Elsevier
• キーワード: compressible two-phase flow, fluid-structure interaction, high-pressure die casting, shot sleeve, critical velocity

2. 要旨:

本稿では、高圧ダイカストにおけるピストン運動の低速段階での臨界プランジャ速度と、それをオープンソースソフトウェアを用いたCFD法でどのように決定できるかを調査します。溶湯-空気系は、空気を圧縮性完全気体として扱うオイラー的なvolume-of-fluidアプローチによりモデル化されます。乱流は、Menter SST k-ωモデルを用いたRANSアプローチにより扱われます。メッシュ移動に関する2つの異なる戦略が提示され、互いに比較されます。ソルバーは、解析モデルおよび実験データにより検証されます。次に、2Dメッシュを用いて最適速度を決定する方法が提示されます。第二段階として、これらの結果が実際の3D形状から得られた結果や、ダイのインゲートシステムのシミュレーション結果とどのように一致するかが議論されます。

3. 緒言:

高圧ダイカスト（HPDC）は、自動変速機ハウジングやギアボックス部品など、大量生産かつ低コストの自動車部品を製造するための重要なプロセスです [1-4]。一般的にアルミニウムまたはマグネシウムである液体金属は、ショットスリーブチャンバーに注入され、さらに複雑なゲートおよびランナーシステムを介して、通常50～100 ms⁻¹の高速で、最大100 MPaの非常に高い圧力下でダイに射出されます。通常の高圧ダイカストプロセスは、一般的に3つの段階で構成されます。これらの段階を次の図に示します（figure 1はこれらの段階を示しています。左から右へ：予備充填、ダイ充填（ショット）、保圧）。本稿の内容は、最初の段階のプロセスを中心に展開されます。

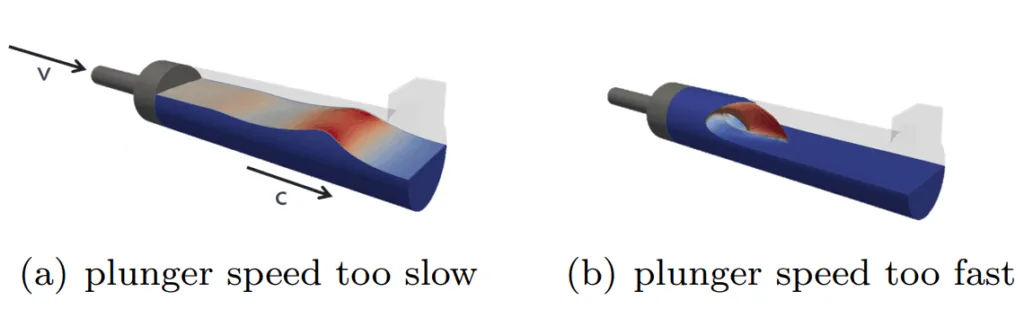
このプロセスの1つの側面は、高圧ダイカストマシンのショットスリーブ内で起こる流動プロセスです。ピストン径、チャンバー内の溶湯高さ、チャンバー長の各組み合わせに対して、解析的に[5, 6]または実験的に[7]決定できる臨界速度が正確に1つ存在します。Fauraらは、その速度に到達するための最適な加速度パラメータも定義しました[6]。健全な鋳造プロセスを達成するためには、プランジャ速度とその加速度プロファイルを慎重に選択する必要があります。Figure 2はこの主張を示しています。右の図では、プランジャはシステムの臨界速度以下で動作しています。空気と溶湯の界面、すなわち波はプランジャから分離し、チャンバー内部を自由に伝播します。これは、最終的な溶湯前面の背後に空気を巻き込み、鋳物内部に欠陥を生じさせる可能性があるため、避けるべきです。

2つの極端なケースをfigure 3にさらに示します。Figure 3(a)は、プランジャ速度が、チャンバー内で蓄積する波が自然に伝播しようとする速度よりもはるかに遅いプロセス設定を示しています。Figure 3(b)はもう一方の極端なケースを示しています。ここでは、プランジャが速すぎます。溶湯はプランジャの前面で、伝播する波が溶湯-プランジャ界面から材料を運び去ることができるよりもはるかに速く蓄積します。その結果、溶湯と空気の界面が円形チャンバーの天井に当たるとすぐに波が砕けます。

これらの図は、各溶湯高さとショットスリーブ径の組み合わせに対して、見つけなければならない適切な速度が1つだけであることを示しています。

4. 研究の概要:

研究テーマの背景:

高圧ダイカスト（HPDC）プロセスには、プランジャがショットスリーブを通して溶融金属を押し出す重要な第一段階が含まれます。この「低速段階」におけるプランジャ速度は、空気の巻き込みと最終的な鋳造品質に大きく影響します。「臨界速度」、すなわち最適なプランジャ速度を決定することは、欠陥を最小限に抑えるために不可欠です。

先行研究の状況:

先行研究には、ショットスリーブ内の臨界速度と波のダイナミクスを決定するための解析モデル[5, 6]、この速度を測定した実験的研究[7]、およびGarber [29]による最適速度と充填度に関する研究が含まれます。KortiとAboudi [21]によるものなど、CFDシミュレーションも溶湯/空気界面のダイナミクス研究に使用されてきました。

研究の目的:

本稿は、オープンソースソフトウェア（OpenFOAM）を用いたCFD法により、HPDCの低速段階における臨界プランジャ速度を調査することを目的としています。目的は以下の通りです。

• ショットスリーブ内の二相（溶湯-空気）流のCFDモデルを開発し、検証する。
• 移動するプランジャを扱うための異なるメッシュ移動戦略を比較する。
• パラメータスタディを通じて2Dメッシュを用いて最適プランジャ速度を決定する。
• インゲートシステムを含む実際の3D形状から得られた結果と2Dの結果との整合性を議論する。

中核的研究:

本研究の中核は以下の通りです。

• 空気を圧縮性完全気体として扱い、乱流をRANS Menter SST k-ωモデルで扱うオイラー的なvolume-of-fluid（VOF）アプローチを用いた溶湯-空気系のモデル化。
• 2つのメッシュ移動戦略（メッシュ圧縮とレイヤー追加/削除、後者を優先）の実装と比較。
• 開発されたソルバーの解析モデル（例：Reikher and Barkhudarov [27]、shallow-water equations [28]）および既存のCFDデータ[21]に対する検証。
• プランジャ速度と巻き込まれた空気の関係を特定し、それによって最適速度範囲を決定するための2Dショットスリーブモデルに関するパラメータスタディの実施。
• 検証されたソルバーを3Dの工業用ショットスリーブ形状（EA211クランクケース）に適用し、より現実的なシナリオでその性能を評価し、知見を確認する。

5. 研究方法論

研究デザイン:

本研究では、数値流体力学（CFD）シミュレーションアプローチを採用しました。この研究には、移動プランジャを組み込んだHPDCショットスリーブ内の二相（溶融金属と空気）圧縮性流れのモデル化が含まれていました。研究デザインには以下が含まれます。

• OpenFOAMを用いたCFDモデルの開発。
• 確立された解析モデルおよび既発表の実験結果とCFD結果に対する数値ソルバーの検証。
• プランジャ速度が空気巻き込みに及ぼす影響を調査するためのパラメトリックスタディ。
• 2D単純化形状と3D実世界工業ケースの両方へのモデルの適用。

データ収集・分析方法:

データは、開発されたOpenFOAMソルバーを用いた数値シミュレーションを通じて生成されました。分析された主要な変数は以下の通りです。

• 溶湯先端がインゲートに到達した時点でショットスリーブ内に巻き込まれた空気の量。
• ショットスリーブ内の溶湯先端の挙動と波の伝播。
• プランジャ部の溶湯高さ。
  広範囲のプランジャ速度についてシミュレーションが実行されました。分析は、空気巻き込みにつながる流れのパターンを特定し、それを最小化する最適な速度範囲を決定することに焦点を当てました。メッシュ移動戦略は、安定性と計算効率について比較されました。

研究テーマと範囲:

主要な研究テーマは、空気巻き込みを最小化するためのHPDCプロセスの低速段階における臨界プランジャ速度の決定でした。範囲には以下が含まれます。

• 圧縮性二相流（液体アルミニウム合金と空気）のモデル化。
• 移動プランジャに関連する流体構造連成のシミュレーション。
• メッシュ移動戦略（メッシュ圧縮 対 レイヤー除去）の調査と比較。
• CFDソルバーの検証。
• 2Dショットスリーブ形状（例：直径130 mm、充填率65%）に関するパラメータスタディ。
• インゲートシステムを含む3D工業用ショットスリーブ形状（VolkswagenのEA211クランクケース）へのソルバーの適用とテスト。

6. 主要な結果:

主要な結果:

• 本研究は、無料で利用可能なオープンソースソフトウェア（OpenFOAM）が、HPDCショットスリーブの低速段階における複雑な流動ダイナミクスを効果的にモデル化できることを示しました。
• 「レイヤー追加および削除」メッシュ移動戦略は、メッシュ圧縮と比較して、シミュレーションにおいてより安定し、計算効率が高いことがわかりました。
• 開発されたCFDソルバーは、Reikher and Barkhudarov [27]によるモデル（shallow-water equations [28]から導出された式(19)）などの解析モデル、およびKorti and Aboudi [21]による既発表のCFDデータ（Figure 7）に対して正常に検証されました。
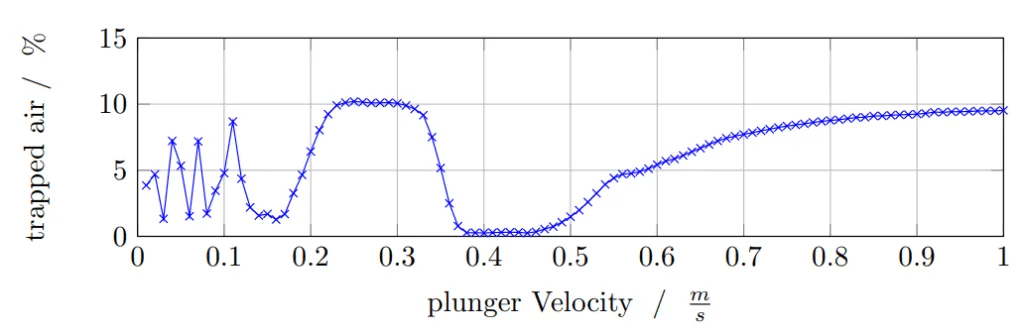
• 2Dショットスリーブ（直径130 mm、充填率65%、長さ1.015 m）の場合、パラメータスタディにより、約0.38 ms⁻¹から0.46 ms⁻¹の最適なプランジャ速度範囲が特定されました（Figure 10）。この範囲は、巻き込まれた空気を最小限に抑え、Garber [29]およびBrunnhuber [2]による実験データ（同様の構成で臨界速度として0.46 ms⁻¹を報告）とよく一致しています。
• プランジャ速度に基づいて、異なる流動様相が特定されました。
  • 遅すぎる（約0.17 ms⁻¹未満）：不安定な波の動き、大きなエアポケットの可能性。
  • やや遅い（約0.23 ms⁻¹ - 0.32 ms⁻¹）：ピストンが波の完全な移動には速すぎるため、溶湯が閉じ込められる。
  • 最適範囲（約0.38 ms⁻¹ - 0.46 ms⁻¹）：波のピークがショットスリーブの天井まで形成され、空気を効果的に押し出す。
  • 速すぎる（0.46 ms⁻¹超）：溶湯が蓄積し、波が砕け、プロセス中に空気を巻き込む。
• プランジャを正確な臨界速度よりもわずかに速く操作する方が、遅すぎて溶湯前面の背後に大きな孤立したエアポケットを閉じ込めるプロセスよりも、（空気巻き込みの観点からは）害が少ないことが観察されました。
• ソルバーは、特定のインゲートシステムを含む3Dの工業用ショットスリーブ形状（EA211クランクケース）に正常に適用されました。結果（Figure 11、Figure 12）は、第一段階でプランジャの速度を最適値に近づけることで、その前面の背後に巻き込まれる空気の量が常に減少することを確認しました。

図の名称リスト:

• Figure 1: Three phases of die filling.
• Figure 2: Impact of increasing plunger propagation according to [1].
• Figure 3: The two extrema of the wrong plunger speed during the first phase of the high-pressure die casting process
• Figure 4: A simplified picture of the basic mesh at t = 0
• Figure 5: A simplified picture of the mesh after an interval of Δt has elapsed and the compression strategy is used
• Figure 6: The process of layer removal during the mesh motion procedure
• Figure 7: Benchmarking of the presented OpenFOAM model with previously published data by Korti and Aboudi [21]; the figure shows the interface positions at various time steps
• Figure 8: Solving process scheme of the two phase VOF-solver
• Figure 9: The melt height at the piston boundary; analytical model according to [27] vs. result of the numerical simulation
• Figure 10: Fraction of trapped air inside the shot sleeve for slow phase velocities between 0 and 1 m/s; parameters according to table 3
• Figure 11: Trapped air for the shot-sleeve in the EA211 crank case application and the corresponding tested plunger law.
• Figure 12: The fraction occupied by air after the meltfront has propagated into the ingate.

7. 結論:

本稿の研究は、高価な商用ソフトウェアツールを必要とせずに、無料で利用可能なオープンソースソフトウェアを用いても、低速段階におけるショットスリーブダイナミクスの計算上かなり複雑な流れの問題をモデル化できることを示しました。文書化された結果は、この問題に関する以前のCFDシミュレーションや、shallow-water equationsから導出された解析モデルとよく一致しています。レイヤー除去アプローチを優先する2つの異なるメッシュ移動戦略が提示されました。ソルバーは最終的に、通常の工業用インゲートシステムが取り付けられた3Dショットスリーブの溶湯流れを解くことができました。一般的に、実際のテストで3D形状に期待される結果を再現することが可能でした。空気巻き込みを減らすためにピストン運動の低速段階で速度を上げるという経済的利点も指摘されました。

8. 参考文献:

• [1] B. Nogowizin, Theorie und Praxis des Druckgusses, Schiele und Schoen, Berlin, 1st edn., ISBN 978-3794907960, 2010.
• [2] E. Brunnhuber, Praxis der Druckgussfertigung, Schiele und Schoen, Berlin, ISBN 978-3794905355, 1991.
• [3] H. Kaufmann, P. Uggowitzer, Metallurgy and processing of high-integrity light metal pressure castings, Fachverlag Schiele & Schön, 2014.
• [4] J. Campbell, Complete Casting Handbook: Metal Casting Processes, Metallurgy, Techniques and Design, Elsevier Science, ISBN 9780081001202, 2015.
• [5] J. López, J. Hernández, F. Faura, G. Trapaga, Shot sleeve wave dynamics in the slow phase of die casting injection, Journal of fluids engineering 122 (2) (2000) 349-356.
• [6] F. Faura, J. López, J. Hernández, On the optimum plunger acceleration law in the slow shot phase of pressure die casting machines, International Journal of Machine Tools and Manufacture 41 (2) (2001) 173–191.
• [7] T. Tszeng, Y. Chu, A study of wave formation in shot sleeve of a die casting machine, Journal of engineering for industry 116 (2) (1994) 175–182.
• [8] C. Hirt, B. Nichols, Volume of fluid (VOF) method for the dynamics of free boundaries, J. Comp. Phys. 39 (1981) 201-225.
• [9] A. Dahle, L. Arnberg, The rheological properties of solidifying aluminum foundry alloys, JOM 48 (3) (1996) 34-37.
• [10] P. Ferrer, D. Causon, L. Qian, C. Mingham, Z. Ma, A multi-region coupling scheme for compressible and incompressible flow solvers for two-phase flow in a numerical wave tank, Computers & Fluids 125 (2016) 116–129.
• [11] R. Mayon, Z. Sabeur, M.-Y. Tan, K. Djidjeli, Free surface flow and wave impact at complex solid structures, in: 12th International Conference on Hydrodynamics, Egmond aan Zee, NL, 18-23 September, 10pp., 2016.
• [12] S. Kohlstädt, M. Vynnycky, A. Neubauer, A. Gebauer-Teichmann, Comparative RANS turbulence modelling of lost salt core viability in high pressure die casting, accepted for publication in Prog. Comp. Fluid Dyn., 2018.
• [13] J. Brackbill, D. Kothe, C. Zemach, A continuum method for modeling surface tension 100 (2) (1992) 335-354.
• [14] H. Rusche, Computational fluid dynamics of dispersed two-phase flows at high phase fractions, Ph.D. thesis, Imperial College London (University of London), 2003.
• [15] H. Versteeg, W. Malalasekera, An Introduction to Computational Fluid Dynamics: The Finite Volume Method, Pearson Education Limited, 2007.
• [16] F. Menter, 2-equation eddy-viscosity turbulence models for engineering applications, AIAA J. 32 (1994) 1598–1605.
• [17] E. Robertson, V. Choudhury, S. Bhushan, D. Walters, Validation of OpenFOAM numerical methods and turbulence models for incompressible bluff body flows, Computers & Fluids 123 (2015) 122-145.
• [18] F. Menter, M. Kuntz, R. Langtry, Ten years of industrial experience with the SST turbulence model, Turbulence, Heat and Mass Transfer 4 (1) (2003) 625-632.
• [19] M. Koch, C. Lechner, F. Reuter, K. Köhler, R. Mettin, W. Lauterborn, Numerical modeling of laser generated cavitation bubbles with the finite volume and volume of fluid method, using OpenFOAM, Computers & Fluids 126 (2016) 71-90.
• [20] F. White, Fluid mechanics, in SI units, McGraw-Hill, 2011.
• [21] A. Korti, S. Abboudi, Numerical simulation of the interface molten metal air in the shot sleeve chambre and mold cavity of a die casting machine, Heat and Mass Transfer 47 (11) (2011) 1465-1478.
• [22] H. Jasak, A. Jemcov, Z. Tukovic, OpenFOAM: A C++ Library for Complex Physics Simulations, in: International Workshop on Coupled Methods in Numerical Dynamics IUC, 2007.
• [23] H. Weller, G. Tabor, H. Jasak, C. Fureby, A tensorial approach to computational continuum mechanics using object orientated techniques, Computers in Physics 12(6) (1998) 620-631.
• [24] H. Jasak, OpenFOAM: open source CFD in research and industry, International Journal of Naval Architecture and Ocean Engineering 1 (2) (2009) 89-94.
• [25] S. Patankar, D. Spalding, A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows, in: Numerical Prediction of Flow, Heat Transfer, Turbulence and Combustion, Elsevier, 54-73, 1983.
• [26] R. Issa, Solution of the implicitly discretised fluid flow equations by operator-splitting, Journal of Computational Physics 62 (1) (1986) 40–65.
• [27] A. Reikher, M. Barkhudarov, Casting: an analytical approach, Springer Science & Business Media, 2007.
• [28] M. Castro, M. Semplice, Third-and fourth-order well-balanced schemes for the shallow water equations based on the CWENO reconstruction, International Journal for Numerical Methods in Fluids 89 (8) (2019) 304-325.
• [29] L. Garber, Theoretical analysis and experimental observation of air entrapment during cold chamber filling, Die Casting Engineer 26 (3) (1982) 14-15.

9. 著作権:

• この資料は、「S. Kohlstädt, M. Vynnycky, S. Goeke, A. Gebauer-Teichmann」による論文です。「On determining the critical velocity in the high-pressure die casting machine's shot sleeve using CFD」に基づいています。
• 論文の出典: [DOI URLプレースホルダー - これは2019年4月25日にElsevierに提出されたプレプリントであるため、利用可能になり次第追加されます]

この資料は上記の論文に基づいて要約されており、商業目的での無断使用は禁止されています。
Copyright © 2025 CASTMAN. All rights reserved.

研究者向けの主な質疑応答

論文の核心的な知見に基づき、6つの質疑応答を作成します。これらの質問は、この分野の研究者が最も関心を持つであろう要点に対応するものです。回答は簡潔で、論文の内容によって直接裏付けられるものとします。

Q1. HPDCショットスリーブの低速段階で臨界速度を決定する主な目的は何ですか？

A1. 主な目的は、ショットスリーブ内の空気が溶湯前面よりも先に効果的に押し出されるようにすることで、溶融金属内の空気巻き込みを最小限に抑え、それによって最終鋳造品の品質を向上させることです（Figure 3およびFigure 10の文脈で議論されています）。

Q2. ショットスリーブ内の溶湯-空気系には、どのCFDモデリングアプローチが採用されましたか？

A2. 本研究では、溶湯-空気系をモデル化するために、オイラー的なvolume-of-fluid（VOF）アプローチが用いられました。空気は圧縮性完全気体として扱われ、乱流はMenter SST k-ωモデルを用いたRANSアプローチにより処理されました（Abstract、Section 2）。

Q3. 本研究で開発されたCFDソルバーはどのように検証されましたか？

A3. ソルバーは、溶湯高さに関するReikher and Barkhudarov [27]のモデル（Figure 9）などの解析モデル、および界面位置に関するKorti and Aboudi [21]による既発表のCFDデータ（Figure 7）とのシミュレーション結果の比較により検証されました。

Q4. 研究された特定の2Dショットスリーブケース（直径130mm、充填率65%、長さ1.015m）で特定された最適なプランジャ速度範囲は何でしたか？

A4. 最適なプランジャ速度範囲は、約0.38 ms⁻¹から0.46 ms⁻¹であることがわかりました。この範囲は、巻き込まれた空気を最小限に抑え、Garber [29]およびBrunnhuber [2]による実験データと一致しています（Section 5.1、Figure 10）。

Q5. プランジャ速度が最適な臨界速度から大幅に逸脱した場合、どのような結果が生じますか？

A5. プランジャの動きが遅すぎると、波がプランジャから分離して自由に伝播し、溶湯前面の背後に大きなエアポケットを閉じ込める可能性があります。プランジャの動きが速すぎると、溶湯が急速に蓄積し、波が砕けて溶湯に空気を巻き込みます（Figure 3、Section 5.1）。

Q6. 2Dシミュレーションからの知見は、より複雑な3Dの工業形状にも適用可能でしたか？

A6. はい、本研究は、ソルバーと臨界速度の理解が、実際の3Dショットスリーブ（EA211クランクケース）とその工業用インゲートシステムに適用可能であることを実証しました。3Dシミュレーションは、最適速度付近での操作が巻き込まれた空気を減少させることを確認しました（Section 5.2、Figure 11、Figure 12）。