ダイカスト金型のランナー最適化設計に関する研究

この論文要約は、[Publisher]に掲載された論文「A runner-optimization design study of a die-casting die」に基づいています。

1. 概要:

  • タイトル: A runner-optimization design study of a die-casting die(ダイカスト金型のランナー最適化設計に関する研究)
  • 著者: C.C Tai, J.C Lin
  • 発表年: 1998年
  • 掲載ジャーナル/学会誌: Journal of Materials Processing Technology, Elsevier Science S.A.
  • キーワード: ランナー最適化、ダイカスト、アブダクティブネットワーク
Fig. 1. Moving cavity block
Fig. 1. Moving cavity block

2. 研究背景:

  • 研究トピックの社会的/学術的背景: ダイカストは、自動車、航空宇宙、エレクトロニクスなど、様々な産業で広く利用されている精密鋳造法であり、高い強度と良好な外観が特徴です。ダイカスト製品の品質は、ゲートシステム、特にランナー設計によって大きく左右されます。従来のダイカストランナー設計は、ダイカスト試験段階で繰り返し修正が行われ、加工時間とコストの増加につながっていました。
  • 既存研究の限界: 従来の研究は、溶湯の流れ、冷却システム、凝固プロセス、金型寿命など、ダイカストの様々な側面に焦点を当ててきました。しかし、金型寿命と鋳造品質に影響を与える主要因である残留応力と温度を最小限に抑えるための効果的なランナー設計手法が求められています。最適なダイカストパラメータを取得するための既存の手法は、しばしば矛盾しており、満足のいく鋳造品質と金型寿命を両立させることが困難でした。
  • 研究の必要性: ランナーシステム設計の最適化は、ダイカストにおける加工時間とコストを削減するために不可欠です。設計段階で温度分布と残留応力を予測することで、鋳造品質と金型寿命のバランスを取ることが可能になります。ダイカストパラメータと性能の間の複雑な関係をモデル化し、効果的なランナー最適化を可能にする堅牢な手法が必要です。

3. 研究目的と研究課題:

  • 研究目的: 本研究の主な目的は、残留応力を最小限に抑え、温度を制御することにより、金型寿命と鋳造品質を向上させるための、ダイカスト金型の最適化されたランナーシステムを設計することです。アブダクティブネットワークとシミュレーテッドアニーリングアルゴリズムを用いたモデリング手法を開発し、この最適化を達成することを目指しています。
  • 主な研究課題:
    • アブダクティブネットワークは、ダイカストパラメータ（高速インジェクタ位置、ランナー射出角度、ランナー断面積比）とダイカスト性能（ランナー残留応力と温度）の間の複雑な関係をモデル化するためにどのように利用できるか？
    • シミュレーテッドアニーリングアルゴリズムは、アブダクティブネットワークモデルと定義された性能指標に基づいて、最適なダイカストパラメータを探索するためにどのように利用できるか？
    • 提案されたランナー最適化設計手法は、ダイカスト金型における残留応力の低減と温度制御にどの程度効果的か？
  • 研究仮説:
    • アブダクティブネットワークは、入力パラメータに基づいてダイカスト性能を正確に予測できる。
    • シミュレーテッドアニーリングアルゴリズムは、残留応力を最小限に抑え、温度を制御する最適なダイカストパラメータを効果的に特定できる。
    • 提案された手法を用いて導き出された最適化ランナー設計は、従来のデザインと比較して、残留応力の低減と金型寿命の向上をもたらす。

4. 研究方法:

  • 研究デザイン: 本研究では、実験計画法と計算モデリングを組み合わせたアプローチを採用しています。ランナーブロックとキャビティブロックを別々に設計・製造し、異なるダイカスト条件下での試験を可能にしました。23種類の異なるインサートランナーブロックを試験しました。
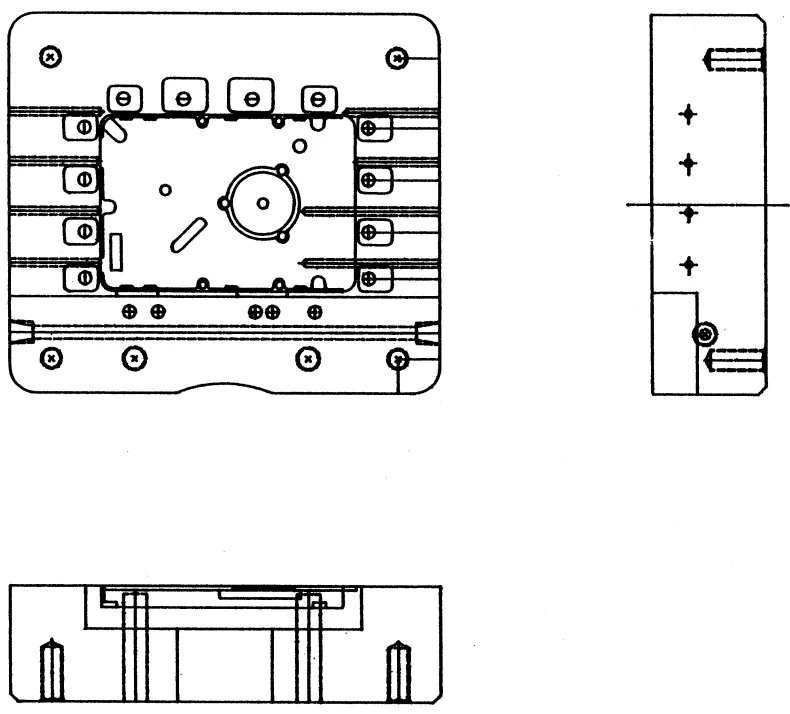
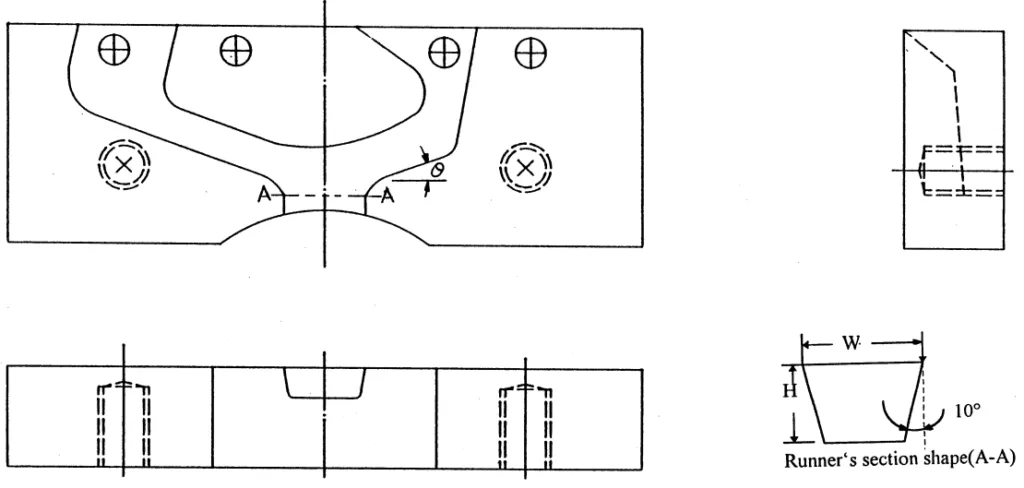
  • データ収集方法: ダイカスト実験は、アルミニウム合金を用いて実施しました。鋳造圧力（117.6 MPa）、射出速度（0.2 m/s および 2.8 m/s）、サイクル時間（3 shots/min）などのダイカストパラメータを制御しました。温度は、熱電対を用いて、可動金型と固定金型のキャビティ表面下の点（図1の点A〜H）で測定しました。残留応力は、ASTM規格に準拠したブラインドホール法を用いて、RS-200ドリル装置とSYSTEM-4000測定システムを用いて、ランナー入口とゲート付近の位置（図2のRS）で測定しました。
  • 分析方法: アブダクティブネットワークを構築し、ダイカストプロセスをモデル化しました。ネットワークは、ダイカストパラメータ（高速インジェクタ位置、ランナー射出角度、ランナー断面積比）を入力として使用し、ダイカスト性能（ランナー残留応力と温度）を予測します。シミュレーテッドアニーリングアルゴリズムを用いて、正規化された温度と残留応力を組み合わせた性能指標に基づいて、最適なダイカストパラメータを最適化しました。最適なネットワーク構造を決定するために、予測二乗誤差（PSE）基準を使用しました。
  • 研究対象と範囲: 本研究は、ダイカスト金型におけるランナーシステム設計に焦点を当てています。実験的研究は、特別に設計された金型とランナーブロックを用いたアルミニウム合金のダイカストを含みます。範囲は、残留応力を最小限に抑え、キャビティ表面付近の温度を制御するための、ランナー設計パラメータ（ランナー射出角度とランナー断面積比）と高速インジェクタ位置の最適化に限定されています。

5. 主な研究結果:

  • 主な研究結果:
    • アブダクティブネットワークは、ダイカストプロセスをモデル化し、温度と残留応力を正確に予測するために開発され、成功しました。予測誤差は、実験測定値と比較して5％以内でした（表5）。
    • シミュレーテッドアニーリングアルゴリズムは、最適なダイカストパラメータを効果的に探索しました。
    • ゲート付近の位置での残留応力は、ランナー入口よりも約100 MPa大きく、ゲート領域が損傷を受けやすいことを示しています。
    • 最大残留応力値は、常に表面層の0.1 mm以内の位置に存在することがわかりました。
    • 鋳造欠陥、主に引け巣と湯回り不良が、異なる実験パラメータ下で観察されました（表2）。
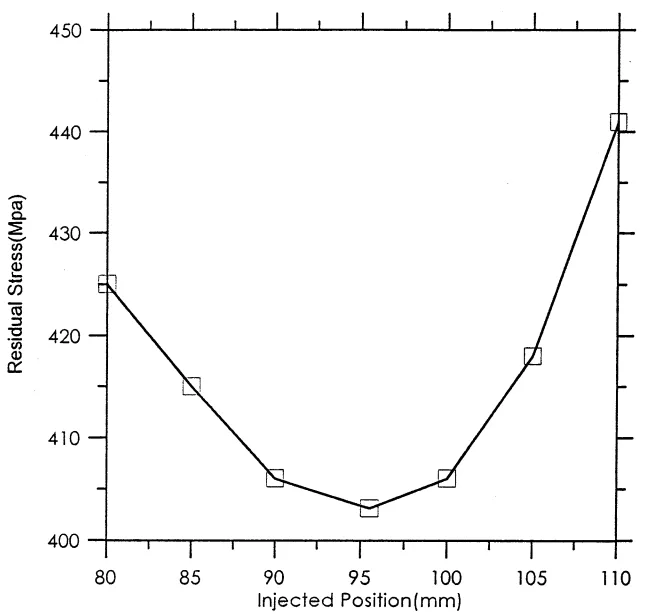
    • 最適化の結果、ランナー断面積比が2.3、重み関数w₁=0、w₂=1の場合、最適な高速インジェクタ位置は95.51 mm、ランナー射出角度は69.1°であり、その結果、最小残留応力は403.1 MPaとなりました（表6）。
    • 射出速度位置が105 mm、w₁=0、w₂=1の場合、最適な射出角度は72.16°、ランナー断面積比は2.85であり、最小残留応力は409 MPaとなりました。
  • 統計的/定性的分析結果:
    • アブダクティブネットワークは、温度で4.2％以内、残留応力で3.8％以内の誤差で、高い予測精度を示しました。
    • シミュレーテッドアニーリングアルゴリズムは、最適なパラメータに収束し、最適化における有効性を示しました。
    • 実験結果（表3および4）は、温度と残留応力の測定値と予測値の良好な一致を示しています。
  • データ解釈: 結果は、アブダクティブネットワークとシミュレーテッドアニーリングアプローチが、ダイカストにおけるランナー設計を最適化するための実行可能な方法であることを示しています。最適化結果に基づいてダイカストパラメータを調整することにより、金型寿命と鋳造品質の向上に不可欠な残留応力の低減と温度制御が可能になります。重み関数（w₁、w₂）により、温度と残留応力の最小化のトレードオフを調整できます。
  • 図表リスト:
    • 図 1. 可動金型ブロック
    • 図 2. インサートランナーブロック
    • 図 3. シミュレーテッドアニーリング探索のフローチャート
    • 図 4. 射出位置調整時の一般的な条件下での最適化におけるダイカストパラメータの影響
    • 図 5. 射出角度調整時の一般的な条件下での最適化におけるダイカストパラメータの影響
    • 図 6. ランナー断面積比調整時の一般的な条件下での最適化におけるダイカストパラメータの影響
Fig. 2. Insert runner block
Fig. 2. Insert runner block
Fig. 4. Effect of die-casting parameters in optimization under general conditions, when adjusting the injected position (w1=0, w2=1; runner sectional ratio, 2.3; runner adjust injected angle, 69.7°; the minimum residual stresses, 403. 1 MPa; injected position, 95.5 mm).
Fig. 4. Effect of die-casting parameters in optimization under general conditions, when adjusting the injected position (w1=0, w2=1; runner sectional ratio, 2.3; runner adjust injected angle, 69.7°; the minimum residual stresses, 403. 1 MPa; injected position, 95.5 mm).

6. 結論と考察:

  • 主な結果の要約: 本研究では、アブダクティブネットワークとシミュレーテッドアニーリングアルゴリズムを用いて、ダイカスト金型のランナー最適化設計手法を開発し、検証に成功しました。この手法は、ダイカストプロセスを効果的にモデル化し、温度と残留応力を予測し、残留応力を最小限に抑え、温度を制御するための最適なダイカストパラメータを特定します。実験的検証により、モデルの精度と最適化アプローチの有効性が確認されました。
  • 研究の学術的意義: 本研究は、ランナーシステム設計の最適化のための新しいアプローチを提供することにより、ダイカストの分野に貢献しています。この文脈におけるアブダクティブネットワークとシミュレーテッドアニーリングの応用は、複雑な製造プロセスをモデル化および最適化するための強力な方法論を示しています。この研究はまた、金型寿命と鋳造品質を向上させるために、金型設計において温度と残留応力の両方を考慮することの重要性を強調しています。
  • 実用的な意義: 提案された手法は、ダイカストメーカーがランナー設計を最適化するための実用的なツールを提供し、コストと時間がかかる試行錯誤のダイカスト試験の必要性を減らします。この手法を使用することで、製造業者は、金型寿命が長く、鋳造品質が向上し、製造コストが削減された金型を設計できます。実証されているように、インサートスタイルのランナーブロックを使用すると、ランナーシステムの簡単かつ費用対効果の高い修正と最適化が可能になります。
  • 研究の限界: 本研究は、特定のダイカストパラメータと材料に限定されています。より広範囲のダイカスト条件、材料、および金型形状にわたって手法を検証するには、さらなる研究が必要です。アブダクティブネットワークモデルの複雑さとシミュレーテッドアニーリングアルゴリズムの計算コストは、リアルタイムアプリケーションまたは非常に複雑な金型設計の場合、制限となる可能性があります。

7. 今後のフォローアップ研究:

  • 今後の研究の方向性:
    • 提案された手法の適用範囲を、異なるダイカスト合金および金型形状に拡張する。
    • ゲート設計や冷却システムパラメータなど、他のダイカストパラメータが最適化プロセスに及ぼす影響を調査する。
    • 計算効率を向上させ、潜在的により優れた最適化結果を達成するために、より高度な最適化アルゴリズムの使用を検討する。
    • 提案された手法に基づいて、産業環境での採用を促進するためのユーザーフレンドリーなソフトウェアツールを開発する。
  • さらなる探求が必要な分野:
    • 最適化されたランナー設計を使用することで達成される長期的な金型寿命の改善は、長期的なダイカスト実験を通じてさらに調査する必要があります。
    • 予測された残留応力と実際の金型破損メカニズム（例：ヒートチェック、亀裂）の関係をより詳細に調査する必要があります。
    • 目的関数の重み係数（w₁、w₂）に対する最適化結果の感度については、異なるアプリケーションシナリオでの選択に関するガイドラインを提供するために、さらなる調査が必要です。

8. 参考文献:

  • [1] T.P. Groeneveld, W.D. Kaiser, Effects of metal velocity and die temperature on metal-flow distance and casting quality, Die Casting Eng. 23 (5) (1979) 44-49.
  • [2] R.L. Trueloved, Die casting temperature control: a new locating waterlines, Die Casting Eng. 26 (1) (1979) 28-31.
  • [3] S.H. Jong, H.Y. Chou, C.R.Li and W.S. Hwang,@ Application of mold filling analysis in the design of die casting die, Chukung Q. 73 (1992) 1-9.
  • [4] S.H. Jong, M.S. Poon, H.Y. Chouand and W.S.Hwang,@ The application of solidification analysis in die casting, Chukung Q. 74 (1992) 1-11.
  • [5] M. Hihara (1992) paper in Japanese.
  • [6] G.J. Montgomery, K.C. Drake, Abductive reasoning network, Neurocomputing 2 (1991) 97-104.
  • [7] S. Kirkpartick, C.D. Gelatt, M.P. Vecchi, Optimization by simulated annealing, Science 220 (4958) (1983) 671-680.
  • [8] S. Geman, D. Geman, Stochastic relaxation, Gibbs distributions and the Bayesian restoration of images, IEEE Trans. Pattern Anal. Mach. Intell. 6 (6) (1984) 721-741.
  • [9] B.W. Lee, B.J. Sheu, Hardware Annealing in Analog VLSI Neurocomputing, Kluwer, Dordrecht, 1991.
  • [10] C. Zhang, H.P. Wang, The discrete tolerance optimal problem, ASME Manuf. Rev. 6 (1) (1991) 60–71.
  • [11] Y.S. Trang, S.C. Ma, L.K. Chung, Determination of optimal cutting parameters in wire electrical discharge machining, Int. J. Mach. Tools Manuf. 35 (12) (1995) 1693-1701.
  • [12] G.A. Miller, The magic number seven, plus or minus two: some limits on our capacity for processing information, Philos. Rev. 63 (8) (1956) 81-87.
  • [13] A.R. Barron, in: S.J. Farlow (Ed.), Predicted Square Error: A Criterion for Automatic Model Selection, Self-Organizing Methods in Modeling: GMDH Type Algorithms, Marcel-Dekker, New York, 1984.
  • [14] N. Metropolis, A. Rosenbluth, M. Rosenbluth, A. Teller, E. Teller, Equation of state calculation by fast computing machines, J. Chem. Phys. 21 (1953) 187-1092.

9. 著作権:

この資料は上記の論文に基づいて要約されたものであり、商業目的での無断使用は禁止されています。
Copyright © 2025 CASTMAN. All rights reserved.

PDF Downloads
Tags: aluminum alloy; ,Applications; ,CAD; ,Die casting; ,Efficiency; ,金型; ,금형; ,자동차; ,해석